Prueba

Ésta es una página de prueba, pueden jugar aqui y modificar para ver que les sale ...

\nabla^{2}

hay que ver la pagina que hizo Elsa

que la guadalupe tiene más visitas que jerusalem.

$\nabla ^{2}\$

Propagación del pulso Gaussiano en la dirección positiva del eje Z

• Esto es una prueba
  • prueba 2
    • prueba 3

• Probando, probando: uno, dos, tres.

Mi firma: --Belen 21:46 20 ene 2009 (CST)lkjhgf--uchija 15:00 16 feb 2009 (CST)

---

que

• ===quefdvvv parffhgnf===

Probando notación

\[Mu] - \[Beta]

\Psi^2 - \[PartialD] x/\[PartialD] t

Archivo:Animatedgauss.GIF

Propagación del pulso Gaussiano en la dirección positiva del eje Z.

--topological_neutrino 02:05 11 oct 2007 (CDT)

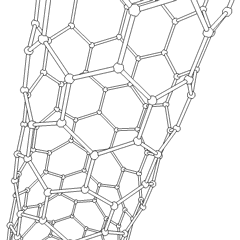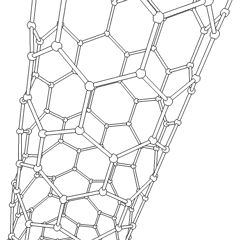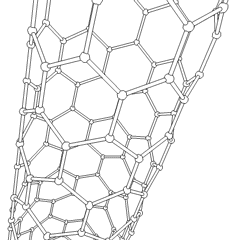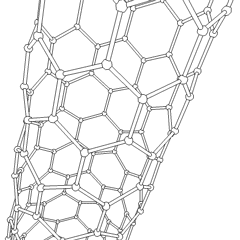
Esta animación de un nanotubo de Carbono muestra su estructura en 3D.

Archivo:Pulgauss.gif

Imagen en formato GIF.

Archivo:Pulgauss.flv

Imagen en formato FLV.

Tierra Rotando.

--topological_neutrino 02:05 11 oct 2007 (CDT)

Medios estratificados - Ecuación diferencial

Manuel Fernández Guasti

Medio estratificado

Medios dieléctricos con permitivdad $\varepsilon$ y permeabilidad $\mu$ dependientes de la posicién. La dependencia espacial esté restringida a una direccién en el caso estratificado (digamos en el eje z ). Ondas monocrométicas linealmente polarizadas.

La ecuaciones de Maxwell son equivalentes ante la transformacién $\mathbf {E} \leftrightarrow \mathbf {H} ,\;\varepsilon \leftrightarrow -\mu$. De manera que solo ondas TE se necesitan analizar en detalle.

Campo Eléctrico

El campo eléctrico de las ecuaciones de Maxwell para un medio estático,

isotrópico y lineal es

$\nabla ^{2}\mathbf {E} -\mu \varepsilon {\frac {\partial ^{2}\mathbf {E} }{\partial t^{2}}}=\nabla \left({\frac {\rho }{\varepsilon _{t}}}\right)-\nabla \left(\mathbf {E} \cdot \nabla \ln \varepsilon \right)+\mu {\frac {\partial \mathbf {J} }{\partial t}}-\nabla \ln \mu \times \nabla \times \mathbf {E} .$

En ausencia de cargas y corrientes

$\nabla ^{2}\mathbf {E} -\mu \varepsilon {\frac {\partial ^{2}\mathbf {E} }{\partial t^{2}}}=-\nabla \left(\mathbf {E} \cdot \nabla \ln \varepsilon \right)-\nabla \ln \mu \times \nabla \times \mathbf {E} .$

Mientras que si el medio esté estratificado en la direccién $z$,

entonces $\varepsilon \left(z\right),\mu \left(z\right)$.

$\nabla ^{2}\mathbf {E} -\mu \varepsilon {\frac {\partial ^{2}\mathbf {E} }{\partial t^{2}}}=-\nabla \left(E_{z}{\frac {\partial \ln \varepsilon }{\partial z}}\right)-{\frac {\partial \ln \mu }{\partial z}}\left({\hat {\mathbf {k} }}\times \nabla \times \mathbf {E} \right).$

Si el campo es TE y la propagación en el plano y-z , entonces $E=E_{x}{\hat {\mathbf {i} }}+E_{y}{\hat {\mathbf {j} }}+E_{z}{\hat {\mathbf {k} }}\rightarrow E=E_{x}\left(y,z\right){\hat {\mathbf {i} }}$.

$\nabla ^{2}E_{x}-\mu \varepsilon {\frac {\partial ^{2}E_{x}}{\partial t^{2}}}={\frac {\partial \ln \mu }{\partial z}}{\frac {\partial E_{x}}{\partial z}}$

puesto que $\nabla \times E_{x}{\hat {\mathbf {i} }}={\frac {\partial E_{x}}{\partial z}}{\hat {\mathbf {j} }}-{\frac {\partial E_{x}}{\partial y}}{\hat {\mathbf {k} }}$ y entonces ${\hat {\mathbf {k} }}\times \nabla \times E_{x}{\hat {\mathbf {i} }}={\hat {\mathbf {k} }}\times {\frac {\partial E_{x}}{\partial z}}{\hat {\mathbf {j} }}=-{\frac {\partial E_{x}}{\partial z}}{\hat {\mathbf {i} }}$.

Si escribimos explécitamente el laplaciano y la dependencia monocromética

${\frac {\partial ^{2}E_{x}}{\partial y^{2}}}+{\frac {\partial ^{2}E_{x}}{\partial z^{2}}}+\mu \varepsilon \omega ^{2}E_{x}={\frac {\partial \ln \mu }{\partial z}}{\frac {\partial E_{x}}{\partial z}},$

donde $\mu \varepsilon \omega ^{2}={\frac {n^{2}}{c^{2}}}\omega ^{2}=n^{2}k_{0}^{2}$. ésta ecuacién \eqref{eq: Hy wave eq strat} es el punto de partida del tratamiento que en el B\&W se obtiene de las ecs. de Maxwell en primeras derivadas.

\subsection[soluciones]{Soluciones de la ecuacién diferencial}

Considere que se pueden separar las variables

$E_{x}\left(y,z\right)=Y\left(y\right)U\left(z\right),$

de manera que se obtiene

${\underset {f\left(z\right)}{\underbrace {{\frac {1}{U}}{\frac {\partial ^{2}U}{\partial z^{2}}}+n^{2}k_{0}^{2}-{\frac {\partial \ln \mu }{\partial z}}{\frac {1}{U}}{\frac {\partial U}{\partial z}}} }}+{\underset {-f\left(y\right)}{\underbrace {{\frac {1}{Y}}{\frac {\partial ^{2}Y}{\partial y^{2}}}} }}=0$

donde hay dos partes que dependen solamente de z y y respectivamente \cite[p. 56]{Born05}. Dado que éstas variables son independientes, cada una debe cumplirse para cualquier valor de la otra variable \footnote{ésta condición proviene de la separacién de variables independientes. }. Sea la funcién constante $f\left(z\right)=-f\left(y\right)=\sigma ^{2}k_{0}^{2}$. La existencia de ésta cantidad invariante es la generalizacién de la relacién de Snell para medios inhomogéneos. Las ecuaciones son

entonces para la variable y

${\frac {1}{Y}}{\frac {\partial ^{2}Y}{\partial y^{2}}}=-\sigma ^{2}k_{0}^{2}\quad \Longrightarrow \quad Y\left(y\right)=Y_{0}\exp \left(i\sigma k_{0}y\right)$

y para la variable en z

${\frac {\partial ^{2}U}{\partial z^{2}}}-{\frac {\partial \ln \mu }{\partial z}}{\frac {\partial U}{\partial z}}+\left(n^{2}k_{0}^{2}-\sigma ^{2}k_{0}^{2}\right)U=0.$

El parametro variable sufre un corrimiento $\Omega ^{2}\rightarrow \Omega ^{2}-\sigma ^{2}k_{0}^{2}$ respecto al caso unidimensional \footnote{Como se veré en la siguiente subseccién, $\sigma =0$ para incidencia normal. }. La ecuacién \eqref{eq: ode U} se resuelve por métodos matriciales en el formalismo de Abeles.

En (nuestro) el formalismo de amplitud y fase, se puede resolver numéricamente ésta ecuacién. Primeramente, eliminar la primera derivada mediante la transformacién $U=u{\sqrt {\mu }}$, como se muestra en el \ref{sec:ap=E9ndice-amplitud}.

La ecuacién para la la variable $u$ es entonces

${\frac {\partial ^{2}u}{\partial z^{2}}}+\left[n^{2}k_{0}^{2}-\sigma ^{2}k_{0}^{2}+\left({\frac {1}{2}}{\frac {\partial ^{2}\ln \mu }{\partial z^{2}}}-{\frac {1}{4}}\left({\frac {\partial \ln \mu }{\partial z}}\right)^{2}\right)\right]u=0.$

El parámetro dependiente de la posicién puede escribirse como

$\kappa _{u}^{2}=\left(n^{2}k_{0}^{2}-\sigma ^{2}k_{0}^{2}\right)+{\frac {1}{2}}{\frac {\ddot {\mu }}{\mu }}+{\frac {1}{4}}{\frac {{\dot {\mu }}^{2}}{\mu ^{2}}};$

La constante $\sigma$ se puede establecer de una regién donde el éndice de refraccién es constante. Si la fase puede escribirse como $\mathbf {k} \cdot \mathbf {r} =\mathbf {k} \cdot \mathbf {y} +\mathbf {k} \cdot \mathbf {z} =\left|\mathbf {k} \right|\left|\mathbf {y} \right|\sin \theta +\left|\mathbf {k} \right|\left|\mathbf {z} \right|\cos \theta$ donde $\left|\mathbf {k} \right|=k_{0}n\left(z\right)$, y el éngulo se mide con respecto a la normal a la superficie estratificada. De

\eqref{eq: ode Y}

$\sigma =n\left(z\right)\sin \theta =n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}.$

Este resultado es consistente con la propagacién en z en una

regién de éndice constante pues

$\left|\mathbf {k} \right|\left|\mathbf {z} \right|\cos \theta =k_{0}nz\cos \theta ={\sqrt {n^{2}k_{0}^{2}-\sigma ^{2}k_{0}^{2}}}.$

Representacién de amplitud y fase

$\int \limits _{C}n_{1}{\vec {s}}_{1}\cdot d{\vec {r}}+$

Si se considera un medio no magnético $\mu =\mu _{0}$, entonces la

ecuacién \eqref{eq: ode u} se simplifica a

${\frac {\partial ^{2}u}{\partial z^{2}}}+\left[n^{2}k_{0}^{2}-\sigma ^{2}k_{0}^{2}\right]u=0.$

La representacién de amplitud y fase nos permite escribir la ecuacién para la amplitud (Ermakov) como

Considere una solucién de la forma $u=A\exp \left(i\phi \right)$ donde la amplitud $A$ y la fase $\phi$ son cantidades reales. La ecuacién

(\ref{eq: ode u sin mu}) deviene en

${\frac {\partial ^{2}A}{\partial z^{2}}}-A\left({\frac {\partial \phi }{\partial z}}\right)^{2}+2i{\frac {\partial A}{\partial z}}{\frac {\partial \phi }{\partial z}}+iA{\frac {\phi }{\partial z^{2}}}=-\left[n^{2}-\sigma ^{2}\right]k_{0}^{2}A$

Para un medio transparente sin abosrcién la permitividad es real.

La parte real de la ecuacién anterior es

${\frac {\partial ^{2}A}{\partial z^{2}}}-A\left({\frac {\partial \phi }{\partial z}}\right)^{2}=-\left[n^{2}-\sigma ^{2}\right]k_{0}^{2}A$

mientras que la parte imaginaria es

$2i{\frac {\partial A}{\partial z}}{\frac {\partial \phi }{\partial z}}+iA{\frac {\partial ^{2}\phi }{\partial z^{2}}}=0.$

ésta éltima ecuacién la escribimos como

${\frac {1}{A}}\left(2A{\frac {\partial A}{\partial z}}{\frac {\partial \phi }{\partial z}}+A^{2}{\frac {\partial ^{2}\phi }{\partial z^{2}}}\right)={\frac {1}{A}}{\frac {\partial \left(A^{2}{\frac {\partial \phi }{\partial z}}\right)}{\partial z}}=0$

de manera que si $A$ no es cero, existe el invariante

$A^{2}{\frac {\partial \phi }{\partial z}}=Q$

Substitucién de este resultado en (\ref{eq: re ode u})

${\frac {\partial ^{2}A}{\partial z^{2}}}-{\frac {Q^{2}}{A^{3}}}=-\left[n^{2}-\sigma ^{2}\right]k_{0}^{2}A$

Esta ecuacién es la ecuacién de Ermakov. Para obtener una ecuacién adimensional se escribe el invariante como $Q=k_{0}A_{0}^{2}$ . La

ecuacién adimensional para la amplitud es entonces

${\frac {1}{k_{0}^{2}}}{\frac {\partial ^{2}A_{d}}{\partial z^{2}}}-{\frac {1}{A_{d}^{3}}}=-\left[n^{2}-\sigma ^{2}\right]A_{d}$

donde $A_{d}=A/A_{0}$ es la amplitud adimensional \footnote{El resultado anterior se puede obtener de proponer una solucién de la forma $u=A\exp[i\int (Q/A^{2})dz]$, donde $Q$ es constante. La

segunda derivada de esta funcién es

${\frac {\partial ^{2}u}{\partial z^{2}}}={\frac {1}{A^{3}}}\left(A^{3}{\frac {\partial ^{2}A}{\partial z^{2}}}-Q^{2}\right)\exp \left(i\int {\frac {Q}{A^{2}}}\partial z\right)=\left({\frac {1}{A}}{\frac {\partial ^{2}A}{\partial z^{2}}}-{\frac {Q^{2}}{A^{4}}}\right)u$

que al sustituir en (\ref{eq: ode u sin mu}) se obtiene de nuevo la ecuacién de Ermakov. }.

En una comunicacién anterior abordamos el problema de incidencia normal

([#References|references]). La ecuacién diferencial a resolverse es

la misma que \ref{eq: ode amp adi} excepto que en incidencia normal, de la ecuacién de \ref{eq: snell} $\sigma =0$. --FJ777 18:48 13 ago 2008 (CDT) --FJ777 18:51 13 ago 2008 (CDT) --FJ777 18:52 13 ago 2008 (CDT) --FJ777 18:54 13 ago 2008 (CDT) --FJ777 18:54 13 ago 2008 (CDT) --FJ777 18:55 13 ago 2008 (CDT) --FJ777 19:47 13 ago 2008 (CDT) --FJ777 19:48 13 ago 2008 (CDT) --FJ777 19:49 13 ago 2008 (CDT) --FJ777 19:50 13 ago 2008 (CDT)

Soluciones de tangente hiperbólica

Permita que la variacién del éndice de refraccién sea

$n\left(z\right)=n_{i}+{\frac {\left(n_{f}-n_{i}\right)}{2}}\left(1+{\mbox{tanh}}\left[{\frac {2}{D}}\arctan \left({\frac {9}{10}}\right)z\right]\right)$

donde $n_{2}$ y $n_{1}$ son los éndices de refraccién en las regiones 1 y 2 lejos de la interfase donde el éndice es constante y el parémetro $D$ corresponde al espesor donde el éndice varéa dentro del 90\ de sus valores iniciales y finales.

La ecuacién diferencial a resolver es entonces

$\left(2\pi \right)^{-2}{\frac {\partial ^{2}A_{d}}{\partial z^{2}}}-{\frac {1}{A_{d}^{3}}}=-\left[n_{i}+{\frac {\left(n_{f}-n_{i}\right)}{2}}\left(1+{\mbox{tanh}}\left[{\frac {2}{D}}\arctan \left({\frac {9}{10}}\right)z\right]\right)\right]^{2}A_{d}$

La condicién de frontera se establece en la condicién final. El problema corresponde a establecer la amplitud transmitida y a partir de dicho resultado encontrar las amplitudes incidentes y reflejadas. No es adecuado establecer la condicién inicial como la amplitud incidente, pues en esa regién existiré simulténeamente una onda reflejada cuyo valor es desconocido ([#References|references]).

Considere que la onda incidente viaja en la direccién positiva de la $z$ y el éndice de refraccién varia alrededor de $z=0$. Las condiciones

iniciales para la ecuacién diferencial son entonces

$\left.{\frac {\partial A_{d}}{\partial z}}\right|_{z=z_{2}}=0,\quad A_{d}\left(z_{2}\right)=A_{t}=\left(n_{f}\right)^{-1/2},\quad z_{2}\gg 0$

donde $A_{t}$ es la amplitud adimensional transmitida lejos de la interfase.

campo magnético -revisar/completar

El campo magnético de las ecuaciones de Maxwell para un medio estético,

isotrépico y lineal es

$\nabla ^{2}\mathbf {H} -\mu \varepsilon {\frac {\partial ^{2}\mathbf {H} }{\partial t^{2}}}=-\nabla \left[\mathbf {H} \cdot \nabla \ln \mu \right]-\nabla \ln \varepsilon \times \left(\nabla \times \mathbf {H} \right)-\varepsilon \nabla \times \mathbf {J} +\nabla \ln \varepsilon \times \mathbf {\mathbf {J} }$

En ausencia de cargas y corrientes

$\nabla ^{2}\mathbf {H} -\mu \varepsilon {\frac {\partial ^{2}\mathbf {H} }{\partial t^{2}}}=-\nabla \left[\mathbf {H} \cdot \nabla \ln \mu \right]-\nabla \ln \varepsilon \times \left(\nabla \times \mathbf {H} \right)$

Mientras que si el medio esté estratificado en la direccién $z$,

entonces $\varepsilon \left(z\right),\mu \left(z\right)$.

$\nabla ^{2}\mathbf {H} -\mu \varepsilon {\frac {\partial ^{2}\mathbf {H} }{\partial t^{2}}}=-\nabla \left(H_{z}{\frac {\partial \ln \mu }{\partial z}}\right)-{\frac {\partial \ln \varepsilon }{\partial z}}\left({\hat {\mathbf {k} }}\times \nabla \times \mathbf {H} \right).$

Si el campo es TE y la propagacién en el plano y-z , entonces

$\mathbf {H} =H_{x}{\hat {\mathbf {i} }}+H_{y}{\hat {\mathbf {j} }}+H_{z}{\hat {\mathbf {k} }}\rightarrow \mathbf {H} =H_{y}\left(y,z\right){\hat {\mathbf {j} }}+H_{z}\left(y,z\right){\hat {\mathbf {k} }}$.

$\nabla ^{2}H_{y}-\mu \varepsilon {\frac {\partial ^{2}H_{y}}{\partial t^{2}}}=-{\frac {\partial H_{z}}{\partial y}}{\frac {\partial \ln \mu }{\partial z}}-{\frac {\partial \ln \varepsilon }{\partial z}}\left({\frac {\partial H_{z}}{\partial y}}-{\frac {\partial H_{y}}{\partial z}}\right)$ $\nabla ^{2}H_{z}-\mu \varepsilon {\frac {\partial ^{2}H_{z}}{\partial t^{2}}}=-{\frac {\partial }{\partial z}}\left(H_{z}{\frac {\partial \ln \mu }{\partial z}}\right)$

puesto que $\nabla \times \left[H_{y}\left(y,z\right){\hat {\mathbf {j} }}+H_{z}\left(y,z\right){\hat {\mathbf {k} }}\right]=\left({\frac {\partial H_{z}}{\partial y}}-{\frac {\partial H_{y}}{\partial z}}\right){\hat {\mathbf {i} }}$ y entonces $\left({\frac {\partial H_{z}}{\partial y}}-{\frac {\partial H_{y}}{\partial z}}\right){\hat {\mathbf {k} }}\times {\hat {\mathbf {i} }}=\left({\frac {\partial H_{z}}{\partial y}}-{\frac {\partial H_{y}}{\partial z}}\right){\hat {\mathbf {j} }}$.

Si escribimos explécitamente el laplaciano y la dependencia monocromética

${\frac {\partial ^{2}H_{y}}{\partial y^{2}}}+{\frac {\partial ^{2}H_{y}}{\partial z^{2}}}+\mu \varepsilon \omega ^{2}H_{y}=-{\frac {\partial H_{z}}{\partial y}}{\frac {\partial \ln \mu }{\partial z}}-{\frac {\partial \ln \varepsilon }{\partial z}}\left({\frac {\partial H_{z}}{\partial y}}-{\frac {\partial H_{y}}{\partial z}}\right),$ ${\frac {\partial ^{2}H_{z}}{\partial y^{2}}}+{\frac {\partial ^{2}H_{z}}{\partial z^{2}}}+\mu \varepsilon \omega ^{2}H_{z}=-{\frac {\partial }{\partial z}}\left(H_{z}{\frac {\partial \ln \mu }{\partial z}}\right).$

donde $\mu \varepsilon \omega ^{2}={\frac {n^{2}}{c^{2}}}\omega ^{2}=n^{2}k_{0}^{2}$.

Invariante

Sean dos soluciones linealmente independientes

$U_{1}'=i\omega \mu V_{1}$ $U_{2}'=i\omega \mu V_{2}$

Del producto de \eqref{eq: U der V 2} por $V_{1}$ menos \eqref{eq: U der V 1}por

$V_{2}$ se obtiene

$V_{1}U_{2}'-V_{2}U_{1}'=0.$

De manera anéloga $V_{1}'=i\omega \left(\varepsilon -{\frac {\alpha ^{2}}{c^{2}\mu }}\right)U_{1}$

y $V_{2}'=i\omega \left(\varepsilon -{\frac {\alpha ^{2}}{c^{2}\mu }}\right)U_{2}$

$U_{1}V_{2}'-U_{2}V_{1}'=0.$

De la diferencia \eqref{eq: U V ders}-\eqref{eq:V U ders} de éstas

dos ecuaciones

$U_{1}V_{2}'+V_{2}U_{1}'-U_{2}V_{1}'-V_{1}U_{2}'={\frac {d}{dz}}\left(U_{1}V_{2}-U_{2}V_{1}\right)=0$

Coeficientes de reflexión y transmisión

Sean $A$, $R$ y $T$ las amplitudes complejas del campo eléctrico incidente, reflejado y transmitido.

Continuidad de las contribuciones tangenciales de los campos $\mathbf {E}$

y $\mathbf {H}$, asi como la relación entre ellos para una onda plana

$\mathbf {H} ={\sqrt {\frac {\varepsilon }{\mu }}}{\hat {\mathbf {k} }}\times \mathbf {E}$

Para una onda TM (transverso eléctrico) plana

$U_{0}=A+R$

Es decir, al incidir en el medio estratificado que inicia en $U\left(z=0\right)=U_{0}$ existe una onda incidente y una reflejada. Nótese que $U$ es el campo eléctrico independiente del tiempo como se describe en la ecuación (5) \cite[sec. 1.6.1, p.52 ]{Born75}. Sin embargo, B\&W se refiere a las amplitudes complejas \cite[sec. 1.6.3, p.59-60]{Born75} iguales a los campos.

$U\left(z_{l}\right)=T$

El campo en la ec. (46) \cite[sec. 1.6.3, p.60]{Born75} se escribe el argumento de $U$ como $z_{1}$ que es la última capa; nosotros preferimos escribir $z_{l}$ (la última capa) donde ya solamente hay onda transmitida.

\bibliographystyle{alpha} \bibliography{/home/mfg/acad/ext/ref/libros-doc,/home/mfg/acad/dif/curri/ref-mias/mfg-arti}

\appendix

== $\alpha$

La primera derivada de \eqref{eq: ode U} se puede eliminar mediante

la transformación $U=u{\sqrt {\mu }}$, entonces la primera derivada es

${\frac {\partial U}{\partial z}}=\mu ^{\frac {1}{2}}{\frac {\partial u}{\partial z}}+{\frac {1}{2}}u\mu ^{-{\frac {1}{2}}}{\frac {\partial \mu }{\partial z}}=\mu ^{\frac {1}{2}}\left({\frac {\partial u}{\partial z}}+{\frac {1}{2}}u{\frac {\partial \ln \mu }{\partial z}}\right)$

mientras que la segunda derivada es

${\frac {\partial ^{2}U}{\partial z^{2}}}={\frac {1}{2}}\mu ^{\frac {1}{2}}{\frac {\partial \ln \mu }{\partial z}}\left({\frac {\partial u}{\partial z}}+{\frac {1}{2}}u{\frac {\partial \ln \mu }{\partial z}}\right)+\mu ^{\frac {1}{2}}\left({\frac {\partial ^{2}u}{\partial z^{2}}}+{\frac {1}{2}}{\frac {\partial u}{\partial z}}{\frac {\partial \ln \mu }{\partial z}}+{\frac {1}{2}}u{\frac {\partial ^{2}\ln \mu }{\partial z^{2}}}\right)$

que podemos reagrupar como

${\frac {\partial ^{2}U}{\partial z^{2}}}=\mu ^{\frac {1}{2}}\left[{\frac {\partial ^{2}u}{\partial z^{2}}}+{\frac {\partial \ln \mu }{\partial z}}{\frac {\partial u}{\partial z}}+\left({\frac {1}{4}}\left({\frac {\partial \ln \mu }{\partial z}}\right)^{2}+{\frac {1}{2}}{\frac {\partial ^{2}\ln \mu }{\partial z^{2}}}\right)u\right]$

La ecuacién diferencial\eqref{eq: ode U} es entonces\begin{multline*} \frac{\partial^{2}u}{\partial z^{2}}+\frac{\partial\ln\mu}{\partial z}\frac{\partial u}{\partial z}+\left(\frac{1}{4}\left(\frac{\partial\ln\mu}{\partial z}\right)^{2}+\frac{1}{2}\frac{\partial^{2}\ln\mu}{\partial z^{2}}\right)u\\ -\frac{\partial\ln\mu}{\partial z}\left(\frac{\partial u}{\partial z}+\frac{1}{2}u\frac{\partial\ln\mu}{\partial z}\right)+\left(n^{2}k_{0}^{2}-\sigma^{2}k_{0}^{2}\right)u=0,\end{multline*}

que simplifica a

${\frac {\partial ^{2}u}{\partial z^{2}}}+\left[n^{2}k_{0}^{2}-\sigma ^{2}k_{0}^{2}+\left({\frac {1}{2}}{\frac {\partial ^{2}\ln \mu }{\partial z^{2}}}-{\frac {1}{4}}\left({\frac {\partial \ln \mu }{\partial z}}\right)^{2}\right)\right]u=0.$

\end{document}

Solo estoy de curioso pero vamos a ver si entendi bien. --FJ777 18:47 13 ago 2008 (CDT)

--Kanon1106 20:56 20 ene 2009 (CST)