Diferencia entre revisiones de «Problema del átomo de hidrógeno»
Sin resumen de edición |
Sin resumen de edición |
||
| Línea 8: | Línea 8: | ||
Así, obtenemos un problema clásico de mecánica de dos cuerpos. Ahora definimos el centro de masa de nuestro sistema, | Así, obtenemos un problema clásico de mecánica de dos cuerpos. Ahora definimos el centro de masa de nuestro sistema, | ||
[[Archivo:Ecuacioncentrodemasa.gif|sinmarco|centro]] | [[Archivo:Ecuacioncentrodemasa.gif|110 px|sinmarco|centro]] | ||
donde '''r'''<sup>e</sup> y '''r'''<small>p</small> se refieren a la posición del electrón y el protón respectivamente. Para un sistema aislado, sin fuerzas externas actuando sobre él, el centro de masa se mueve a velocidad constante por lo tanto si expresamos la posición de ambas partículas en función de la posición centro de masa '''R''' y sus posiciones relativas, | donde '''r'''<sup>e</sup> y '''r'''<small>p</small> se refieren a la posición del electrón y el protón respectivamente. Para un sistema aislado, sin fuerzas externas actuando sobre él, el centro de masa se mueve a velocidad constante por lo tanto si expresamos la posición de ambas partículas en función de la posición centro de masa '''R''' y sus posiciones relativas, | ||
[[Archivo:Posición electrón.gif|sinmarco|centro]] | [[Archivo:Posición electrón.gif|110 px|sinmarco|centro]] | ||
[[Archivo:Posicionproton.gif|sinmarco|centro]] | [[Archivo:Posicionproton.gif|110 px|sinmarco|centro]] | ||
es claro que hemos reducido el problema a una variable, la posición relativa r, por lo que podemos resolver el sistema clásicamente introduciendo la variable de masa reducida | es claro que hemos reducido el problema a una variable, la posición relativa r, por lo que podemos resolver el sistema clásicamente introduciendo la variable de masa reducida | ||
[[Archivo:CodeCogsEqn (3).gif|sinmarco|centro]] | [[Archivo:CodeCogsEqn (3).gif|110 px|sinmarco|centro]] | ||
Aunque la complejidad del problema se ha reducido es necesario hacer algunas aclaraciones. Aplicando métodos de solución clásicos encontraríamos una respuesta más bien trivial en la medida que el electrón y el protón se atraen hasta colisionar. Por otro lado, si le otorgamos al electrón suficiente momento para establecer una órbita alrededor del núcleo, ésta no duraría mucho tiempo ya que las partículas cargadas aceleradas emiten radiación por lo que un protón en órbita circular bajo los efecto de la aceleración centrípeta, rápidamente se precipitaría al núcleo por la pérdida de energía cinética y el resultante decaimiento de su órbita. | Aunque la complejidad del problema se ha reducido es necesario hacer algunas aclaraciones. Aplicando métodos de solución clásicos encontraríamos una respuesta más bien trivial en la medida que el electrón y el protón se atraen hasta colisionar. Por otro lado, si le otorgamos al electrón suficiente momento para establecer una órbita alrededor del núcleo, ésta no duraría mucho tiempo ya que las partículas cargadas aceleradas emiten radiación por lo que un protón en órbita circular bajo los efecto de la aceleración centrípeta, rápidamente se precipitaría al núcleo por la pérdida de energía cinética y el resultante decaimiento de su órbita. | ||
| Línea 27: | Línea 27: | ||
A partir de aquí es necesario introducir la ecuación de Schrödinger dependiente del tiempo, | A partir de aquí es necesario introducir la ecuación de Schrödinger dependiente del tiempo, | ||
[[Archivo:CodeCogsEqn (4).gif|sinmarco|centro]] | [[Archivo:CodeCogsEqn (4).gif|110 px|sinmarco|centro]] | ||
sin embargo el potencial de Coulomb no depende explícitamente del tiempo así que propondré una solución de la forma | sin embargo el potencial de Coulomb no depende explícitamente del tiempo así que propondré una solución de la forma | ||
[[Archivo:CodeCogsEqn (5).gif|sinmarco|centro]] | [[Archivo:CodeCogsEqn (5).gif|110 px|sinmarco|centro]] | ||
La parte temporal de la solución es una función periódica exponencial y compleja mientras que la ecuación de Schrödinger independiente del tiempo se asocia a la parte espacial y es por lo tanto la ecuación que me interesa resolver, enunciada cómo: | La parte temporal de la solución es una función periódica exponencial y compleja mientras que la ecuación de Schrödinger independiente del tiempo se asocia a la parte espacial y es por lo tanto la ecuación que me interesa resolver, enunciada cómo: | ||
[[Archivo:CodeCogsEqn (6).gif||sinmarco|centro]] | [[Archivo:CodeCogsEqn (6).gif|110 px|sinmarco|centro]] | ||
== Método de diferencias finitas == | == Método de diferencias finitas == | ||
| Línea 40: | Línea 40: | ||
El método de diferencias finitas se utiliza para resolver numéricamente ecuaciones diferenciales. La definición de la derivada en forma de límite es: | El método de diferencias finitas se utiliza para resolver numéricamente ecuaciones diferenciales. La definición de la derivada en forma de límite es: | ||
[[Archivo:CodeCogsEqn.gif|sinmarco|centro]] | [[Archivo:CodeCogsEqn.gif|110 px|sinmarco|centro]] | ||
Lo que busco es aproximar el operador diferencial con pequeñas diferencias. Bajo éste esquema, el dominio de la función está discretizado en escalones finitos de h. Haciendo el desplazamiento h cada vez menor se obtiene una aproximación arbitrariamente precisa. Así, para aumentar la precisión de éste método podemos considerar una cantidad mayor de valores cercanos. Para la segunda derivada, | Lo que busco es aproximar el operador diferencial con pequeñas diferencias. Bajo éste esquema, el dominio de la función está discretizado en escalones finitos de h. Haciendo el desplazamiento h cada vez menor se obtiene una aproximación arbitrariamente precisa. Así, para aumentar la precisión de éste método podemos considerar una cantidad mayor de valores cercanos. Para la segunda derivada, | ||
| Línea 48: | Línea 48: | ||
Ahora puedo, a manera de ejemplo, utilizar éste método para tratar la ecuación de onda de una partícula en una caja, | Ahora puedo, a manera de ejemplo, utilizar éste método para tratar la ecuación de onda de una partícula en una caja, | ||
[[Archivo:Part en caja.svg|sinmarco|centro]] | [[Archivo:Part en caja.svg|sinmarco|110 px|centro]] | ||
Voy a discretizar el dominio utilizando escalones de valor h. La solución es la lista de valores Ψ(0), Ψ(h), Ψ(2h),...,Ψ((N+1)h). Para estos valores, puedo expresar una ecuación de la forma, | Voy a discretizar el dominio utilizando escalones de valor h. La solución es la lista de valores Ψ(0), Ψ(h), Ψ(2h),...,Ψ((N+1)h). Para estos valores, puedo expresar una ecuación de la forma, | ||
[[Archivo:Part en caja 2.svg|sinmarco|centro]] | [[Archivo:Part en caja 2.svg|sinmarco|110 px|centro]] | ||
Donde N+2 es el número total de puntos en el dominio discretizado. Utilizando la forma del método de diferencias finitas para segundas derivadas se obtiene, | Donde N+2 es el número total de puntos en el dominio discretizado. Utilizando la forma del método de diferencias finitas para segundas derivadas se obtiene, | ||
[[Archivo:Disc ej.svg|sinmarco|centro]] | [[Archivo:Disc ej.svg|sinmarco|110 px|centro]] | ||
Notemos que el sistema de ecuaciones puede expresarse como la ecuación matricial, | Notemos que el sistema de ecuaciones puede expresarse como la ecuación matricial, | ||
[[Archivo:Eqn matr.svg|sinmarco|centro]] | [[Archivo:Eqn matr.svg|sinmarco|110 px|centro]] | ||
Se ha obtenido un problema de eigenvalores; al resolverlo se determinan los eigenvectores Ψ que representan la solución así como los eigenvalores que representan los niveles escalonados de energía. Con respecto a las condiciones de frontera, la función de onda de una partícula en una caja debe cumplir las condiciones de frontera de Dirilecht Ψ<sub>0</sub>=Ψ<sub>N+1</sub>=0. Ésto implica dos soluciones triviales pero separadas para los valores Ψ<sub>0</sub> y Ψ<sub>N+1</sub>. Cómo el valor es 0 por diseño, el operador no se ve afectado por su presencia y se pueden implementar condiciones de frontera igual a 0 ignorando los valores Ψ<sub>0</sub> y Ψ<sub>N+1</sub>, reteniendo las N ecuaciones del dominio discretizado. | Se ha obtenido un problema de eigenvalores; al resolverlo se determinan los eigenvectores Ψ que representan la solución así como los eigenvalores que representan los niveles escalonados de energía. Con respecto a las condiciones de frontera, la función de onda de una partícula en una caja debe cumplir las condiciones de frontera de Dirilecht Ψ<sub>0</sub>=Ψ<sub>N+1</sub>=0. Ésto implica dos soluciones triviales pero separadas para los valores Ψ<sub>0</sub> y Ψ<sub>N+1</sub>. Cómo el valor es 0 por diseño, el operador no se ve afectado por su presencia y se pueden implementar condiciones de frontera igual a 0 ignorando los valores Ψ<sub>0</sub> y Ψ<sub>N+1</sub>, reteniendo las N ecuaciones del dominio discretizado. | ||
| Línea 67: | Línea 67: | ||
Ahora voy a aplicar el método para la ecuación radial que se deriva resolviendo la ecuación de Schrödinger, | Ahora voy a aplicar el método para la ecuación radial que se deriva resolviendo la ecuación de Schrödinger, | ||
[[Archivo:CodeCogsEqn (1).gif|sinmarco|centro]] | [[Archivo:CodeCogsEqn (1).gif|110 px|sinmarco|centro]] | ||
Utilizaré la sustitución, | Utilizaré la sustitución, | ||
[[Archivo:Sust rad shr.gif|sinmarco|centro]] | [[Archivo:Sust rad shr.gif|110 px|sinmarco|centro]] | ||
Así, el operador diferencial queda cómo | Así, el operador diferencial queda cómo | ||
[[Archivo:Svg dif op.svg|sinmarco|centro]] | [[Archivo:Svg dif op.svg|110 px|sinmarco|centro]] | ||
[[Archivo:Svg 2.svg|sinmarco|centro]] | [[Archivo:Svg 2.svg|110 px|sinmarco|centro]] | ||
Dividiendo entre r, | Dividiendo entre r, | ||
[[Archivo:Svgentrer.svg|sinmarco|centro]] | [[Archivo:Svgentrer.svg|110 px|sinmarco|centro]] | ||
y ahora dividiendo por la constante del segundo término, | y ahora dividiendo por la constante del segundo término, | ||
[[Archivo:Svg 3 final.svg|sinmarco|centro]] | [[Archivo:Svg 3 final.svg|110 px|sinmarco|centro]] | ||
| Línea 94: | Línea 94: | ||
Discretizaré la coordenada radial usando una red equidistante r<sub>i</sub> con N elementos y un desplazamiento igual a h=r<sub>i+1</sub>-r<sub>i</sub>. El Hamiltoniano discretizado consiste de 3 términos donde el primero se corresponde con el operador de Laplace | Discretizaré la coordenada radial usando una red equidistante r<sub>i</sub> con N elementos y un desplazamiento igual a h=r<sub>i+1</sub>-r<sub>i</sub>. El Hamiltoniano discretizado consiste de 3 términos donde el primero se corresponde con el operador de Laplace | ||
[[Archivo:Matriz a.svg|sinmarco|centro|mat]] | [[Archivo:Matriz a.svg|110 px|sinmarco|centro|mat]] | ||
junto con otras dos matrices diagonales, | junto con otras dos matrices diagonales, | ||
[[Archivo:Matc.svg|sinmarco|centro]] | [[Archivo:Matc.svg|110 px|sinmarco|centro]] | ||
[[Archivo:Matrizb.svg|sinmarco|centro|mat disc]] | [[Archivo:Matrizb.svg|110 px|sinmarco|centro|mat disc]] | ||
La suma de estas 3 matrices representa la matriz hamiltoniana que se quiere diagonalizar para resolver el problema de eigenvalores. Los eigenvalores son los estados energéticos y sus eigenvectores ρ están relacionados a la parte radial de la ecuación de onda del hidrógeno gracias a la sustitución que adoptamos antes, ρ= rR. | La suma de estas 3 matrices representa la matriz hamiltoniana que se quiere diagonalizar para resolver el problema de eigenvalores. Los eigenvalores son los estados energéticos y sus eigenvectores ρ están relacionados a la parte radial de la ecuación de onda del hidrógeno gracias a la sustitución que adoptamos antes, ρ= rR. | ||
Revisión del 19:01 10 jun 2021
Resumen
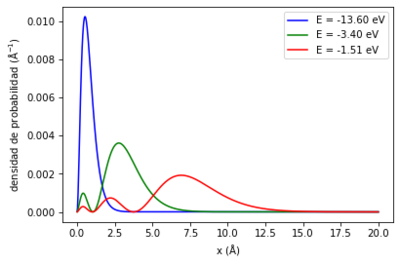
En este texto propongo el método de diferencias finitas para obtener una solución numérica del problema del átomo de hidrógeno, es decir, resolver la ecuación de Schrödinger independiente del tiempo. Finalmente implementé el método en python para obtener una representación gráfica de la probabilidad de densidad de la posición del electrón en función de su distancia al núcleo.
Planteamiento del problema
Considere un átomo de hidrógeno con un electrón de carga -e y masa me y un protón con carga +e y masa mp. Dadas las propiedades del sistema, en particular, que mp>>me, tomaremos al protón cómo una partícula cargada con un comportamiento cómo se describiría clásicamente. Así, obtenemos un problema clásico de mecánica de dos cuerpos. Ahora definimos el centro de masa de nuestro sistema,
donde re y rp se refieren a la posición del electrón y el protón respectivamente. Para un sistema aislado, sin fuerzas externas actuando sobre él, el centro de masa se mueve a velocidad constante por lo tanto si expresamos la posición de ambas partículas en función de la posición centro de masa R y sus posiciones relativas,
es claro que hemos reducido el problema a una variable, la posición relativa r, por lo que podemos resolver el sistema clásicamente introduciendo la variable de masa reducida
Aunque la complejidad del problema se ha reducido es necesario hacer algunas aclaraciones. Aplicando métodos de solución clásicos encontraríamos una respuesta más bien trivial en la medida que el electrón y el protón se atraen hasta colisionar. Por otro lado, si le otorgamos al electrón suficiente momento para establecer una órbita alrededor del núcleo, ésta no duraría mucho tiempo ya que las partículas cargadas aceleradas emiten radiación por lo que un protón en órbita circular bajo los efecto de la aceleración centrípeta, rápidamente se precipitaría al núcleo por la pérdida de energía cinética y el resultante decaimiento de su órbita.
Así, hemos planteado uno de los problemas fundacionales de lo que hoy se conoce cómo mecánica cuántica: si la teoría clásica nos dice que el átomo de hidrógeno no debería ser estable, ¿por qué lo es?
Solución cuántica
A partir de aquí es necesario introducir la ecuación de Schrödinger dependiente del tiempo,
sin embargo el potencial de Coulomb no depende explícitamente del tiempo así que propondré una solución de la forma
La parte temporal de la solución es una función periódica exponencial y compleja mientras que la ecuación de Schrödinger independiente del tiempo se asocia a la parte espacial y es por lo tanto la ecuación que me interesa resolver, enunciada cómo:
Método de diferencias finitas
El método de diferencias finitas se utiliza para resolver numéricamente ecuaciones diferenciales. La definición de la derivada en forma de límite es:
Lo que busco es aproximar el operador diferencial con pequeñas diferencias. Bajo éste esquema, el dominio de la función está discretizado en escalones finitos de h. Haciendo el desplazamiento h cada vez menor se obtiene una aproximación arbitrariamente precisa. Así, para aumentar la precisión de éste método podemos considerar una cantidad mayor de valores cercanos. Para la segunda derivada,
lo que obtengo es una diferencia de diferencias, por lo tanto es conveniente considerar al menos 3 puntos en mi aproximación: x-h, x, x+h.
Ahora puedo, a manera de ejemplo, utilizar éste método para tratar la ecuación de onda de una partícula en una caja,
Voy a discretizar el dominio utilizando escalones de valor h. La solución es la lista de valores Ψ(0), Ψ(h), Ψ(2h),...,Ψ((N+1)h). Para estos valores, puedo expresar una ecuación de la forma,
Donde N+2 es el número total de puntos en el dominio discretizado. Utilizando la forma del método de diferencias finitas para segundas derivadas se obtiene,
Notemos que el sistema de ecuaciones puede expresarse como la ecuación matricial,
Se ha obtenido un problema de eigenvalores; al resolverlo se determinan los eigenvectores Ψ que representan la solución así como los eigenvalores que representan los niveles escalonados de energía. Con respecto a las condiciones de frontera, la función de onda de una partícula en una caja debe cumplir las condiciones de frontera de Dirilecht Ψ0=ΨN+1=0. Ésto implica dos soluciones triviales pero separadas para los valores Ψ0 y ΨN+1. Cómo el valor es 0 por diseño, el operador no se ve afectado por su presencia y se pueden implementar condiciones de frontera igual a 0 ignorando los valores Ψ0 y ΨN+1, reteniendo las N ecuaciones del dominio discretizado.
Solución radial de la ecuación de Schrödinger independiente del tiempo
Ahora voy a aplicar el método para la ecuación radial que se deriva resolviendo la ecuación de Schrödinger,
Utilizaré la sustitución,
Así, el operador diferencial queda cómo
Dividiendo entre r,
y ahora dividiendo por la constante del segundo término,
Discretización de la coordenada radial por diferencias finitas
Discretizaré la coordenada radial usando una red equidistante ri con N elementos y un desplazamiento igual a h=ri+1-ri. El Hamiltoniano discretizado consiste de 3 términos donde el primero se corresponde con el operador de Laplace
junto con otras dos matrices diagonales,
La suma de estas 3 matrices representa la matriz hamiltoniana que se quiere diagonalizar para resolver el problema de eigenvalores. Los eigenvalores son los estados energéticos y sus eigenvectores ρ están relacionados a la parte radial de la ecuación de onda del hidrógeno gracias a la sustitución que adoptamos antes, ρ= rR.
Implementación en Python
Para esta simulación elegí el número de momento angular cuántico l = 0. Por lo tanto en la gráfica se muestran resultados para los primeros 3 niveles energéticos del átomo de hidrógeno (1s,2s,3s,...). Se sabe que para estos estados corresponden energías de 1 Ry, 1/4 Ry, 1/9 Ry respectivamente lo cual es exactamente lo que se obtiene en la simulación.
Modificar el valor de l no influye en el espectro de energía obtenido, con la excepción de que elimina ciertos estados energéticos. Esto se debe a que para un número cuántico principal n, los valores permitidos de l son 0,1,...,n-1. Es decir que si elegimos l=1 la solución de menor energía corresponde a n=2.
Referencias
Kong, Q., Siauw, T., & Bayen, A. (2020). Python Programming and Numerical Methods: A Guide for Engineers and Scientists (1st ed.). Academic Press.
Schroeder, D. V. (2015). The radial equation. In The radial equation (pp. 1–2). https://physics.weber.edu/schroeder/quantum/RadialEquation.pdf
CODATA Value: Rydberg constant times hc in eV. (2018). The NIST Reference on Constants, Units, and Uncertainty. https://physics.nist.gov/cgi-bin/cuu/Value?rydhcev