Optica: color
La visión de los colores es quizás, el más valioso regalo de la naturaleza. Su origen se considera por algunos adjunto al campo de la Física. El color no es una propiedad intrínseca de los objetos. La materia es totalmente incorpórea. El color no existe y lo que hace que un objeto sea percibido con un determinado color, responde por una parte, a las propiedades de la luz incidentes en el objeto. Sin embargo, nuestra vida está rodeada de colores, aunque en realidad las percepciones del color son simplemente la captación y procesamiento del ojo y cerebro de un determinado haz de luz.
Teorías físicas del color
Muchos pensadores y científicos han estudiado el fenómeno del color, preocupados por comprender su naturaleza y establecer un método para su estudio.
Isaac Newton
Antes de Newton, Descartes ya había intentado descomponer la luz pero sólo logró obtener los colores rojo y azul. En 1666 Isaac Newton tuvo la primer evidencia de que el color no existe. Empleó un par de prismas de vidrio y preparó una estancia en total oscuridad. A través de un agujero en la ventana entraba un rayo de luz solar, colocando el prisma delante del rayo de luz, de modo que lo atravesara y reflejara la luz en la pared opuesta, a 7 metros de distancia. El resultado fue la aparición del arco iris como consecuencia de la refracción de la luz blanca. Hizo converger esos mismos rayos de color en un segundo prisma, a 3 metros de distancia del primero, para formar nuevamente luz blanca. Demostrando que la suma de todos los colores da como resultado el color blanco.
Johann Wolfgang Von Goethe
Un siglo más tarde, después de los experimentos de Newton, el filósofo y escritor alemán mantuvo que la luz solar era pura y que cuando esta se sometía a aflicciones o medios algo opacos y nebulosos, las superficies absorbían parte de la luz blanca y por esta causa, se podían ver los colores. Tratándose del efecto de absorción y reflexión de las superficies.
Arthur Schopenhauer
Discípulo de Goethe, propuso la teoría de que el color blanco se produce en la retina del ojo cuando se recibe una acción plena; ante la ausencia de acción el color resultante es negro. Cuando vemos un color luminosos y cerramos los ojos, observamos la aparición de la postimagen de un color, proponiendo parejas de colores complementarios.
Thomas Young
Afirmó que la luz blanca se podía simplificar en tres colores básicos: azul, rojo y verde. Para demostrarlo, utilizó seis linternas con las luces del arco iris: violeta, azul, verde, amarillo, naranja y rojo. Al mezclar esta luces comprobó que los tres colores de luz básicos podían obtener el resto de los colores.
James Clerk Maxwell
Demostró que la luz es una forma de energía que se propaga por dos campos, uno eléctrico y otro magnético, y que al igual que los rayos X, la radio o el radar, se transmite a gran velocidad, en línea recta y formando ondas. Para medir la longitud de onda, es decir, la distancia entre las crestas de la longitud y su altura, se utiliza como unidad de medida el nanometro(nm).
Heinrich Hertz
Produjo ondas electromagnéticas y las detecto a cierta distancia, comprobando que estas se reflejaban, refractaban y difractaban como las ondas luminosas.
La luz
Se puede definir de una manera muy básica como la radiación que emiten algunos cuerpos. La naturaleza de la luz se ha explicado mediante la teoría corpuscular y la teoría ondulatoria.
A principios del S.XIX, la luz fue considerada como una corriente de partículas (corpúsculos), emitidos por una fuente luminosa la cual estimula el órgano de la vista. Esta teoría fue desarrollada por Isaac Newton y mejorada posteriormente con el modelo cuántico de Max Planck, en el cual los corpúsculos representan cantidades discretas de energía denominadas fotones.
Por otra parte, en el S.XVII varios científicos como Christiaan Huygens, Francesco Grimaldi o Thomas Young, evidenciaron mediante diversos experimentos que la luz era una especie de movimiento ondulatorio con frecuencia, longitud de onda y velocidad de propagación, determinada: teoría ondulatoria de la luz.
En 1873, James C. Maxwell demostró que la luz era una forma de ondas electromagnéticas de alta frecuencia y predijo que las ondas debían tener una velocidad de aproximadamente $300 000$ km/s. En 1887, Heinrich Hertz confirmó experimentalmente la teoría de Maxwell, al generar y detectar por primera vez las ondas electromagnéticas. Posteriormente, él y otros investigadores comprobaron que las ondas electromagnéticas mostraban todos lo fenómenos característicos de la luz.
La luz como onda electromagnética
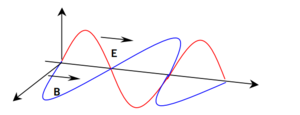
Las radiaciones electromagnéticas se propagan en forma de dos ondas vectoriales mutuamente acopladas y perpendiculares entre si; una onda para el campo eléctrico E y otra para el campo magnético B, tal como se observa en la figura 4.
Según la teoría ondulatoria, la luz se propaga en forma de ondas que viajan en el espacio libre con una velocidad constante $c=3$x$10^8$ m/s. En esta teoría se considera fuente de luz a toda radiación electromagnética cuya longitud varia de $380$nm y $780$nm, o cuya frecuencia oscila entre los $3.2$x$10^{14}$ Hz y $7.7$x$10^{14}$ Hz.
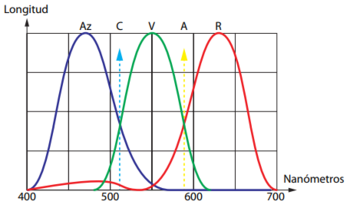
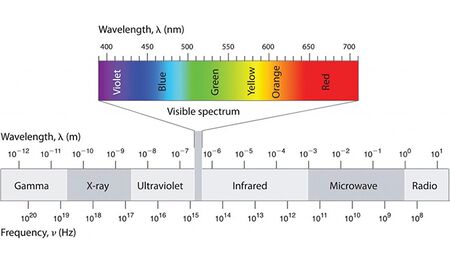
El ojo humano es sensible a las radiaciones electromagnéticas cuya longitud de onda esta comprendida entre los $380$nm y $780$nm aproximadamente. La radiación infrarroja está presente junto a la luz roja, mientras que la radiación ultravioleta se puede observar junto al color violeta. Estas radiaciones son visibles para el ser humano. El espectro visible contiene numerosos colores que son distinguidos por la longitud de onda. El ser humano puede llegar a distinguir hasta aproximadamente $10 000$ colores. La combinación de todas las radiaciones de la luz produce luz blanca, como la procedente de la luz.
Cada onda luminosa monocromática lleva asociada una energía, el fotón, cuyo valor es igual al producto:
\begin{equation} Q=hf \end{equation}
donde $h$ es la constante de Planck, igual a $6.26$x$10^{-24}$ J/s y $f$ es la frecuencia de la onda.
La óptica del color (La percepción del color a través del ojo)
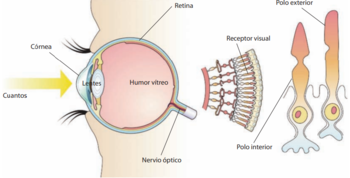
Es importante comprender como una onda electromagnética (luz) se convierte en un impulso eléctrico. La luz viaja por el espacio en forma de ondas. Estas ondas están compuestas por pequeñas unidades de energía denominadas cuantos. Cuando entra un cuanto en el glóbulo ocular, éste atraviesa la córnea y pasa a través de los lentes, llegando a una sustancia gelatinosa llamada humor vítreo, lo atraviesa hasta hasta llegar a la retina que esta en el fondo del glóbulo ocular. En la retina, el cuanto alcanza a un receptor visual, que es estimulado.
Los receptores visuales son unas células con dos polos que se encargan de traducir la luz blanca en señal eléctrica para enviarla al cerebro por medio del nervio óptico. Estas células suman 120 millones de bastoncillos que traducen la luz y 6 millones de conos que traducen los colores. Los conos y los bastoncillos tiene un polo en contacto con la retina. Cuando llega la luz, la parte exterior de los conos y de los bastones se llena de una sustancia que llega al otro polo transformando la información en una descarga eléctrica.
En la retina existen tres tipos de conos conocidos como L [Long(Largos)], M [Middle(Medias)] y S [Short(Cortos)] longitudes de onda. Los conos L son sensibles a tonalidades rojas, los conos M se sensibilizan con tonalidades verdes y los conos S responden a estímulos azules. Cuando el ojo se excita con un espectro luminoso de energía constante ($Q_e(\lambda)=cte$), denominado espectro equienergético, se percibe el blanco. Las percepciones individuales de los colores, ofrecidas por la sensibilización de los conos se dan en las fórmulas siguientes:
\begin{equation} L=\int \varsigma(\lambda)Q_e(\lambda)\, d\lambda \end{equation}
\begin{equation} M=\int \gamma(\lambda)Q_e(\lambda)\, d\lambda \end{equation}
\begin{equation} S=\int \beta(\lambda)Q_e(\lambda)\, d\lambda \end{equation}
donde $\varsigma(\lambda)$, $\gamma(\lambda)$ y $\beta(\lambda)$ representan los valores de conversión de energía radiante en percepción de los conos L, M y S, respectivamente para la longitud de onda $\lambda$.
Percepción del fotón
Estudios recientes han dilucidado cómo la absorción de un fotón en una celda de bastón o cono conduce a la generación de la señal neuronal amplificada que se transmite a neuronas visuales de orden superior. Un pigmento visual fotoexcitado activa la transducina de la proteína de unión a GTP, que a su vez estimula la cGMP fosfodiesterasa. Esta enzima hidroliza cGMP, permitiendo canales catiónicos activados por cGMP en la superficie membrana para cerrar, hiperpolarizar la célula y modular liberación del transmisor en la terminal sináptica. La cinética de reacciones en la cascada cGMP limitan la resolución temporal del sistema visual en su conjunto, mientras que las fluctuaciones estadísticas en las reacciones limitan la fiabilidad de detección de luz tenue.[1]
Interacción de la luz con la materia
Para una explicación física de la cromaticidad de los cuerpos que nos rodean es necesario estudiar la interacción de la luz con la materia de la que están compuestos los objetos. Según el Modelo Corpuscular, la luz está formada por cantidades cuantificables de energía, los fotones. La interacción de la luz (fotones) con los materiales cumple las leyes de conservación de la energía, por lo que la energía radiante que incide sobre un objeto se transforma, por una parte, en energía reflejada, en energía transmitida y en energía absorbida:
\begin{equation} \phi(\lambda)=R(\lambda)+T(\lambda)+A(\lambda) \end{equation}
Donde $\phi(\lambda)$ representa a la luz incidente sobre el objeto, $R(\lambda)$ a la energía reflejada, $T(\lambda)$ al flujo transmitido y $A(\lambda)$ a la cantidad de luz absorbida por la materia. Normalizando estas cantidades, obtenemos:
\begin{equation} 1=\frac{R(\lambda)}{\phi(\lambda)}+\frac{T(\lambda)}{\phi(\lambda)}+\frac{A(\lambda)}{\phi(\lambda)} \end{equation}
Por lo tanto:
\begin{equation} 1 =R + T + A \end{equation}
siendo $R$ la reflectancia, $T$ la transmitancia y $A$ la absortancia, características que definen las propiedades de un material. El valor de estas características depende, por un lado, de la composición química de los cuerpos u objetos y, por otro, de la longitud de onda incidente sobre ellos.
Otro fenómeno es la reflexión interna total, ocurre cuando un rayo en el material a incide sobre un segundo material b cuyo indice de refracción es menor que el material a (es decir $n_b<n_a$). Recordando que si el ángulo de incidencia para el cual un rayo refractado emerge en forma tangencial a la superficie se llama ángulo crítico $\theta_a$. Entonces se puede obtener el ángulo crítico para dos materiales dados $a$ y $b$ si se iguala $\theta_b=90°$ ($\mathrm{sen} (\theta_b)=1 $) en la relación de Snell. [2] De esta forma se tiene:
\begin{equation}
\mathrm{sen}\theta_c=\frac{n_b}{n_a}
\end{equation}
Según sea la longitud de onda que reflejen, transmitan o absorban así será el color con el que se percibe el objeto. Un material que absorba todas las frecuencias (reflectancia y transmitancia nulas) se percibirá negro, mientras que un cuerpo que refleje todas las longitudes de onda visibles (transmitancia y absortancia nulas) aparecerá blanco. En los objetos opacos la transmitancia es insignificante, siendo las frecuencias que refleja el cuerpo las que determinan con que color se va a percibir. En los transparentes, por el contrario, son la reflectancia y la absortancia las que valen prácticamente cero. La reflectancia y la transmitancia son inversamente proporcionales: un objeto con elevada reflectancia para una longitud de onda determinada tendrá escasa transmitancia para esa misma frecuencia, y viceversa. En consecuencia, una especificación puramente objetiva del color de una superficie puede expresarse en términos de reflectancia espectral. En el caso de disoluciones o materiales transparentes dicha especificación vendrá dada por la transmitancia espectral.
Representación del color
Mezcla de colores del espectro
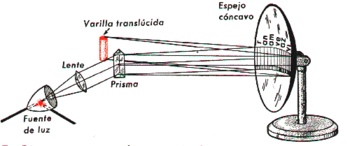
Considerando el experimento que se ve en la figura 7, donde un haz angosto de luz blanca, procedente de un arco de carbón y una lente, incide sobre un prisma de vidrio y se dispersa hacia afuera formando un espectro completo. Con el prisma colocado cerca del centro de la curvatura de un gran espejo cóncavo, todos los colores después de la reflexión son enfocados sobre una varilla traslúcida de vidrio, donde, combinados de nuevo, producen luz blanca. Se sostiene después una tarjeta blanca grande delante del espejo, para que actúe como pantalla y regule los colores que se dejan mezclar en la varilla. Suprimiendo, por ejemplo, el violeta, azul y verde, los colores restantes, rojo, naranja y amarillo, llegan juntos y la varilla se ve anaranjada.
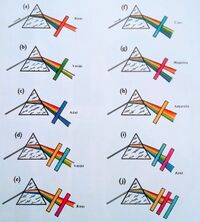
Ahora, dividiendo al espectro en tres partes iguales, llamando a estas como colores primarios aditivos. Cuando se permite la mezcla del rojo y naranja, la varilla se ve de un rojo brillante; cuando se unen el amarillo y el verde, aparece verde brillante; cuando se combinan el azul y el violeta, se observa el azul violáceo. Estos colores aditivos primarios, rojo verde y azul se presentan como las tres grandes superficies circulares en la parte superior izquierda de la figura 8.
El siguiente paso es mezclar los colores primarios, dos a dos, y observar el color resultante de su mezcla. Cuando el rojo primario y el verde primario se combinan en la varilla de vidrio, producen amarillo; rojo y azul dan lugar a magenta, verde y azul producen cían, un azul verdoso claro. Estos, llamados colores primarios sustractivos, se indican con los tres grandes círculos en la parte superior derecha de la figura, y por las áreas de superposición en la parte superior izquierda. Los colores puros del espectro que forman cada primario sustractivo, se muestran en la parte inferior derecha.[3]
Método aditivo de mezcla de colores
Cuando sobre nuestro ojo incide una determinada radiación, sea una única frecuencia o sea un conjunto de varias frecuencias, percibimos algo que denominamos color. Si modificamos la radiación, añadiéndole una o varias frecuencias más, hemos realizado una mezcla aditiva, pues sobre el ojo incide, aparte de la primitiva radiación, las radiaciones nuevas que le hemos añadido. Si se combinan dos fuentes de luz con densidades espectrales de potencia (luminancia) $C_1(\lambda)$ y $C_2(\lambda)$, la luz resultante, $C(\lambda)$, se obtiene como:
\begin{equation}
{C(\lambda)}={C_1(\lambda)}+{C_2(\lambda)}
\end{equation}
Como las luces se suman, este método recibe el nombre de "Sistema Aditivo de Color". De este modo, si sumamos fuentes luminosas con diferentes longitudes de onda $(\lambda)$, podemos generar muchos colores diferentes. Existen tres colores denominados primarios del sistema de mezcla aditiva de color, que son el Rojo, el Verde y el Azul. La razón por la que se utilizan estos colores es que combinándolos de forma adecuada se puede conseguir una gamma de colores distinto más amplia que para otras combinaciones. [4]
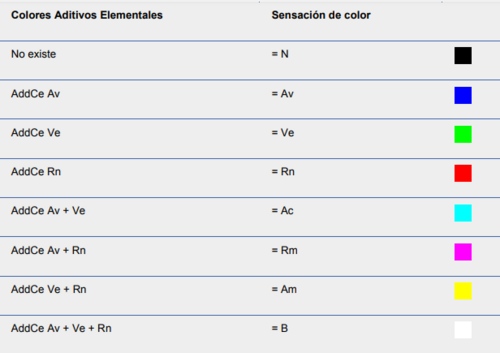
Un ejemplo claro de esto es la denominada televisión a color con el sistema RGB(rojo, verde y azul), en el cual resultan ocho sensaciones extremas del color:
Método sustractivo de mezcla de colores
Consiste en eliminar componentes espectrales de la radiación para conseguir nuevos colores, por ejemplo mediante el filtrado o sustracción de algunas longitudes de onda y reflejando otras. Este proceso, denominado sustracción, se produce porque ciertas moléculas (denominadas pigmentos) absorben zonas particulares del espectro luminoso. Los pigmentos se quedan con unas ciertas longitudes de onda, y una mezcla de dos tipos diferentes de pigmentos dará como resultado una luz reflejada con menos longitudes de onda. Los tres Colores Primarios de los sistemas sustractivos son el Amarillo, el Cyan y el Magenta, que son los colores complementarios de los sistemas aditivos. Mezclando las cantidades adecuadas de estos tres colores podemos conseguir una amplia gama de colores. Si los mezclamos en proporciones iguales obtenemos como resultado el color Negro (Bl) (en este caso, los pigmentos absorben todas las longitudes de onda).
En comparación con la Mezcla Aditiva la Mezcla Sustractiva tiene lugar en un sitio anterior (área del material) en la cadena de efectos entre la luz y la sensación de color. Se relaciona por el poder de absorción del material translúcido. El color Blanco (B) es necesario como color base para llenar las diferencias. Cada capa cromática transparente tiene la misión de absorber en una área del espectro. Para de esta manera activar la fuerza referente de sensación. [5]
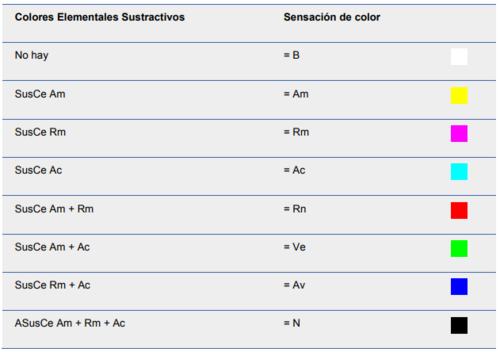
Las 8 sensaciones extremas que son los 8 Colores Elementales se originan en la Mezcla Sustractiva de la siguiente manera:
Leyes de Grassman
Los diversos experimentos de hace ya muchos años sobre mezclas aditivas de colores fueron estudiados por Hermann Günter Grassman y se conocen como leyes de Grassman. Estas leyes dan lugar a otras propiedades importantes en la igualación del color:
1.- Para especificar una mezcla de color son necesarias y suficientes tres variables independientes. De aquí el nombre de "triestímulo" y de "colorimetría tricromática" y el principio según el cual todos los tonos de color pueden igualarse con una adecuada mezcla de tres triestímulos diferentes, siendo la única condición a la hora de elegirlos que ninguno de ellos pueda obtenerse (igualarse) como mezcla de otros dos. Matemáticamente se puede expresar:
\begin{equation} c(C)= r(R) + g(G) + b(B) \end{equation}
donde r,g,b son la luminancia, en lúmenes, de tres fuentes de referencia RGB necesarias para igualar c lúmenes de un color dado C. Lo esencial de esta ley es que existe una y sólo una combinación de tres primarios que igualan cualquier color percibido.
2.- Los estímulos que evocan la misma apariencia de color producen resultados idénticos en mezclas aditivas de colores.Este segundo principio significa que estímulos características físicas diferentes, por ejemplo con distribuciones espectrales de radiancia (flujo radiante), pueden igualar el mismo color. Estos estímulos que físicamente diferentes que permiten la misma igualación de color se llaman metámeros y el fenómeno llamado metamerismo se presenta cuando una misma igualación de color consiste en diferentes componentes de la mezcla. Matemáticamente puede expresarse como sigue:
\begin{equation} c_1(C_1)= r_1(R) + g_1(G) + b_1(B) c_2(C_2)= r_2(R) + g_2(G) + b_2(B) \end{equation}
si
\begin{equation}
c_1(C_1) = c_2(C_2)
\end{equation}
entonces
\begin{equation}
r_1(R) + g_1(G) + b_1(B) = r_2(R) + g_2(G) + b_2(B)
\end{equation}
3.- En una ecuación de color la igualdad no varía si ambos miembros se multiplican por una constante $K$ (ley de proporcionalidad). Esto supone que una vez igualado un estímulo las proporciones de cada componente de la mezcla aditiva no cambia cuando lo hace la luminancia del estímulo de color.
4.- Si se suman dos colores cualesquiera, evaluados con los mismos estímulos de referencia, la suma algebraica de ambos es equivalente a la suma algebraica de las cantidades de los estímulos de referencia necesarios para igualar los colores en cuestión (ley de aditividad). Matemáticamente se expresa:
\begin{equation} c_1(C_1)= r_1(R) + g_1(G) + b_1(B) c_2(C_2)= r_2(R) + g_2(G) + b_2(B) \end{equation}
entonces \begin{equation} c_1(C_1) + c_2(C_2)=(r_1 + r_2)(R)+ (g_1 + g_2)(G) + (b_1 + b_2)(B) \end{equation}
Este conjunto de propiedades se conoce como leyes de las mezclas cromáticas o leyes de Grassman. Ahora bien, una igualación de color no resulta afectada por una exposición previa a la luz (sea ésta blanca o coloreada) o por un cambio de adaptación si se modifica laluminancia del "test que hay que igualar". Este hecho, conocido como principio de persistencia de las igualaciones de color, deja de cumplirse para niveles de luminancia altos,lo que implica que la ley de proporcionalidad también deja de cumplirse.
De la trivariancia visual se puede deducir que es necesario mezclar tres colores para reproducir cualquier otro. Naturalmente, la mezcla debe hacerse en una proporción adecuada de los tres colores, y los tres números que expresan la proporción de mezcla deberán servir para caracterizar el color reproducido. A partir de esta simple idea, desarrollaremos un sistema de coordenadas en el que cada color real (tanto monocromático como de espectro continuo) vendrá definido por tres números.
En el sistema CIE (1931) se toman como primario un sistema basado en tres colores primarios ideales (no reales) obtenidos mediante una transformación matricial del tipo
\begin{equation} [X]= a_11[R]+ a_12[G]+ a_13[B] \end{equation} \begin{equation} [Y]= a_21[R]+ a_22[G]+ a_23[B] \end{equation} \begin{equation} [Z]= a_31[R]+ a_32[G]+ a_33[B] \end{equation}
que diera como resultado el que una de las curvas colorimétricas fuera igual, o muy parecida, a la eficiencia luminosa espectral y que las ordenadas fueran todas positivas. Dando como resultado la siguiente gráfica [6]:
Referencias
- ↑ Dowling John, Stryer Lubert and Wiesel Torsen, "Vision: From Photon to Perception",National Academy of Sciences,(May 20-22, 1995).
- ↑ Hummel, Rolf E. Electronic Properties of Materials. New York: Springer, 2011. Print.
- ↑ https://demoweb.physics.ucla.edu/content/color-mixing, UCLA Physics & Astronomy, Instructional Resource Lab
- ↑ Grassmann H., "Zur Theorie der Farbenmischung", Physikalischen Gesellschaft zu Stettin, (1853).
- ↑ Küppers Harald, Fundamentos de la teoría de los colores,Barron's Educational Series Inc., (1978).
- ↑ https://www.unirioja.es/cu/fede/color_de_vino/capitulo03.pdf