Diferencia entre revisiones de «Optica: Paraxial»
(Nueva página: = aproximación paraxial: soluciones Gaussianas = manuel fernández guasti ==ecuación diferencial== La ecuación de onda<center><math> \nabla^{2}\psi-\frac{1}{v^{2}}\frac{\part...) |
|||
| (No se muestran 97 ediciones intermedias de 7 usuarios) | |||
| Línea 1: | Línea 1: | ||
''' aproximación paraxial: soluciones Gaussianas ''' | |||
==Ecuación diferencial de onda paraxial== | |||
La [[Ondas: ecuacion de onda|ecuacion de onda]] | |||
(1.1)<center><math>{\color{Sepia}\nabla^{2}\psi-\frac{1}{v^{2}}\frac{\partial^{2}\psi}{\partial t^{2}}=0},</math></center> | |||
para una onda monocromática | |||
<math>\psi\left(\mathbf{r},t\right)=\psi\left(\mathbf{r}\right)\exp\left(-i\omega t\right)</math> deviene en la ecuación de Helmholtz | |||
(1.2)<center><math>\nabla^{2}\psi+\kappa^{2}\psi=0,</math></center> | |||
La | |||
\nabla^{2}\psi-\frac{1}{v^{2}}\frac{\partial^{2}\psi}{\partial t^{2}}=0 | |||
para una onda monocromática <math>\psi\left(\mathbf{r},t\right)=\psi\left(\mathbf{r}\right)\exp\left(-i\omega t\right)</math> | |||
deviene en la ecuación de Helmholtz <center><math> | |||
\nabla^{2}\psi+ | |||
donde <math>\omega^{2}/v^{2}=k^{2}</math>. | donde <math>\omega^{2}/v^{2}=k^{2}</math>. | ||
Considere que la onda se propaga preferencialmente en la dirección z, | |||
(1.3)<center><math> | |||
\psi=\tilde{u}\exp\left(ikz\right),</math></center> | |||
donde <math>\tilde{u}</math> es un campo complejo <ref> Siegman A., ''Lasers'', University Science Books, 1986 [cap.16 p. 626] </ref>. El gradiente es entonces | |||
(1.4)<center><math> | |||
\nabla\left[\tilde{u}\exp\left(ikz\right)\right]=\left(\nabla\tilde{u}+ik\tilde{u}\hat{e}_{z}\right)\exp\left(ikz\right),</math></center> | |||
y el laplaciano escrito como la divergencia del gradiente es | |||
(1.5)<center><math> | |||
\nabla^{2}\left[\tilde{u}\exp\left(ikz\right)\right]=\left[\nabla\cdot\left(\nabla\tilde{u}+ik\tilde{u}\hat{e}_{z}\right)\right]\exp\left(ikz\right)+\nabla\left[\exp\left(ikz\right)\right]\cdot\left(\nabla\tilde{u}+ik\tilde{u}\hat{e}_{z}\right),</math></center> | |||
pero | |||
(1.6)<center><math> | |||
\nabla^{2}\left[\tilde{u}\exp\left(ikz\right)\right]=\left[\nabla^{2}\tilde{u}+ik\frac{\partial\tilde{u}}{\partial z}\right]\exp\left(ikz\right)+\left[ik\frac{\partial\tilde{u}}{\partial z}-k^{2}\tilde{u}\right]\exp\left(ikz\right),</math></center> | |||
de manera que | |||
(1.7)<center><math> | |||
\nabla^{2}\left[\tilde{u}\exp\left(ikz\right)\right]=\left[\nabla^{2}\tilde{u}+2ik\frac{\partial\tilde{u}}{\partial z}-k^{2}\tilde{u}\right]\exp\left(ikz\right).</math></center> | |||
La [[Radiacion: Guias de onda|ecuación de Helmhlotz]] (sin aproximaciones aún) es entonces | |||
La ecuación de Helmhlotz (sin aproximaciones aún) es entonces<center><math> | (1.8)<center><math> | ||
\nabla^{2}\tilde{u}+2ik\frac{\partial\tilde{u}}{\partial z}=0. | \nabla^{2}\tilde{u}+2ik\frac{\partial\tilde{u}}{\partial z}+\tilde{u}+(\kappa^{2}-k^{2}) \tilde{u}=0.</math></center> | ||
La aproximación paraxial requiere que <center><math> | La aproximación paraxial requiere que <math>\kappa^{2}-k^{2}= 0</math> y | ||
\left|\frac{\partial^{2}\tilde{u}}{\partial z^{2}}\right|\ll\left|2ik\frac{\partial\tilde{u}}{\partial z}\right|,\left|\frac{\partial^{2}\tilde{u}}{\partial x^{2}}\right|,\left|\frac{\partial^{2}\tilde{u}}{\partial y^{2}}\right| | (1.9)<center><math> | ||
\left|\frac{\partial^{2}\tilde{u}}{\partial z^{2}}\right|\ll\left|2ik\frac{\partial\tilde{u}}{\partial z}\right|,\left|\frac{\partial^{2}\tilde{u}}{\partial x^{2}}\right|,\left|\frac{\partial^{2}\tilde{u}}{\partial y^{2}}\right|.</math></center> | |||
El operador nabla se puede expresar en términos de un operador transversal | El operador nabla se puede expresar en términos de un operador transversal | ||
<math>\nabla_{T}</math> mas un operador longitudinal <math>\frac{\partial}{\partial z}\hat{e}_{z}</math>. | <math>\nabla_{T}</math> mas un operador longitudinal <math>\frac{\partial}{\partial z}\hat{e}_{z}</math>. | ||
En coordenadas cartesianas <math>\nabla_{T}=\frac{\partial}{\partial x}\hat{e}_{x}+\frac{\partial}{\partial y}\hat{e}_{y}</math> | En coordenadas cartesianas <math>\nabla_{T}=\frac{\partial}{\partial x}\hat{e}_{x}+\frac{\partial}{\partial y}\hat{e}_{y}</math> | ||
o en coordenadas cilíndricas <math>\nabla_{T}=</math> <math>\frac{\partial}{\partial\rho}\hat{e}_{\rho}+\frac{1}{\rho}\frac{\partial}{\partial\theta}\hat{e}_{\theta}</math>. | o en coordenadas cilíndricas <math>\nabla_{T}=</math> <math>\frac{\partial}{\partial\rho}\hat{e}_{\rho}+\frac{1}{\rho}\frac{\partial}{\partial\theta}\hat{e}_{\theta}</math>. | ||
De manera que el laplaciano | De manera que el laplaciano se puede sustituir por el laplaciano transversal para obtener la ecuación de onda paraxial | ||
por el laplaciano transversal para obtener la ecuación de onda paraxial<center><math> | (1.10)<center><math> | ||
\nabla_{T}^{2}\tilde{u}+2ik\frac{\partial\tilde{u}}{\partial z}=0 | {\color{Sepia}\nabla_{T}^{2}\tilde{u}+2ik\frac{\partial\tilde{u}}{\partial z}=0},</math></center> | ||
que es una ecuación parabólica. | que es una ecuación parabólica. | ||
==Solución de onda esférica== | |||
Una solución ''exacta'' de la ecuación de onda son las ondas esféricas | |||
(2.1)<center><math> | |||
Una solución ''exacta'' de la ecuación de onda son las ondas esféricas<center><math> | \psi_{esf}=\frac{A_{0}}{r}e^{ikr}.</math></center> | ||
\psi_{esf}=\frac{A_{0}}{r}e^{ikr}. | Demostración: El gradiente de la magnitud radial es <math>\nabla r=\hat{\mathbf{r}}</math>. De manera que | ||
Demostración: El gradiente de la magnitud radial es <math>\nabla r=\hat{\mathbf{r}}</math>. | (2.2)<center><math> | ||
De manera que <center><math> | |||
\nabla\psi_{esf}=\left(-\frac{A_{0}}{r^{2}}\hat{\mathbf{r}}+\frac{A_{0}}{r}ik\hat{\mathbf{r}}\right)e^{ikr}=\left(-\frac{1}{r}+ik\right)\hat{\mathbf{r}}\psi_{esf}.</math></center> | \nabla\psi_{esf}=\left(-\frac{A_{0}}{r^{2}}\hat{\mathbf{r}}+\frac{A_{0}}{r}ik\hat{\mathbf{r}}\right)e^{ikr}=\left(-\frac{1}{r}+ik\right)\hat{\mathbf{r}}\psi_{esf}.</math></center> | ||
El laplaciano es entonces<center><math> | El laplaciano es entonces | ||
\nabla^{2}\psi_{esf} | (2.3)<center><math> | ||
\nabla^{2}\psi_{esf} = \nabla\cdot\left[\left(-\frac{1}{r}+ik\right)\hat{\mathbf{r}}\psi_{esf}\right] | |||
= \left(-\frac{1}{r}+ik\right)\psi_{esf}\nabla\cdot\hat{\mathbf{r}}+\nabla\left[\left(-\frac{1}{r}+ik\right)\psi_{esf}\right]\cdot\hat{\mathbf{r}},</math></center> | |||
pero <math>\nabla\cdot\hat{\mathbf{r}}=2/r</math> y | |||
(2.4)<center><math> | |||
\nabla\left[\left(-\frac{1}{r}+ik\right)\psi_{esf}\right]\cdot\hat{\mathbf{r}}=\frac{1}{r^{2}}\psi_{esf}+\left(-\frac{1}{r}+ik\right)^{2}\psi_{esf},</math></center> | |||
de manera que el laplaciano deviene | |||
(2.5)<center><math> | |||
\nabla^{2}\psi_{esf}=\left[\frac{2}{r}\left(-\frac{1}{r}+ik\right)+\frac{2}{r^{2}}-2\frac{ik}{r}-k^{2}\right]\psi_{esf}=-k^{2}\psi_{esf},</math></center> | |||
y se satisface la ecuación de onda monocromática.<math>\square</math> | |||
== | ==Solución aproximada de ecuación de onda== | ||
La expansión de la distancia radial <math>r=\sqrt{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}+\left(z-z_{1}\right)^{2}}</math> | La expansión de la distancia radial <math>r=\sqrt{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}+\left(z-z_{1}\right)^{2}}</math> | ||
| Línea 66: | Línea 67: | ||
es | es | ||
<center><math> | (3.1)<center><math> | ||
r\approx\left(z-z_{1}\right)+\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2\left(z-z_{1}\right)}.</math></center> | r\approx\left(z-z_{1}\right)+\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2\left(z-z_{1}\right)}.</math></center> | ||
La solución aproximada del resultado esférico exacto es entonces<center><math> | La solución aproximada del resultado esférico exacto es entonces | ||
\psi_{esf}^{aprox}=\frac{A_{0}}{\left(z-z_{1}\right)}\exp\left(ik\left(z-z_{1}\right)\right)\exp\left(ik\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2\left(z-z_{1}\right)}\right)</math></center> | (3.2)<center><math> | ||
Si se expresa ésta ecuación en términos de la forma preferencial \ | \psi_{esf}^{aprox}=\frac{A_{0}}{\left(z-z_{1}\right)}\exp\left(ik\left(z-z_{1}\right)\right)\exp\left(ik\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2\left(z-z_{1}\right)}\right).</math></center> | ||
se obtiene<center><math> | Si se expresa ésta ecuación en términos de la forma preferencial <math> | ||
\tilde{u}=\frac{A_{0}}{\left(z-z_{1}\right)}\exp\left(ik\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2\left(z-z_{1}\right)}\right) | {\color{OliveGreen}\psi=\tilde{u}\exp\left(ik(z-z_{1})\right)}</math>, se obtiene | ||
(3.3)<center><math> | |||
\tilde{u}=\frac{A_{0}}{\left(z-z_{1}\right)}\exp\left(ik\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2\left(z-z_{1}\right)}\right).</math></center> | |||
===Solución exacta de la ecuación paraxial=== | |||
Éste resultado es la solución exacta a la ecuación diferencial aproximada. | |||
Demostración: El gradiente transversal es | |||
(3.1.1)<center><math> | |||
\nabla_{T}\tilde{u}=\frac{ik}{\left(z-z_{1}\right)}\tilde{u}\left[\left(x-x_{1}\right)\hat{e}_{x}+\left(y-y_{1}\right)\hat{e}_{y}\right],</math></center> | |||
y el laplaciano transversal | |||
(3.1.2)<center><math> | |||
\nabla_{T}^{2}\tilde{u} = \frac{ik}{\left(z-z_{1}\right)}\tilde{u}\nabla_{T}\cdot\left[\left(x-x_{1}\right)\hat{e}_{x}+\left(y-y_{1}\right)\hat{e}_{y}\right] | |||
+\left[\frac{ik}{\left(z-z_{1}\right)}\nabla_{T}\tilde{u}\right].\left[\left(x-x_{1}\right)\hat{e}_{x}+\left(y-y_{1}\right)\hat{e}_{y}\right],</math></center> | |||
que puede escribirse como | |||
(3.1.3)<center><math> | |||
\nabla_{T}^{2}\tilde{u}=\frac{2ik}{\left(z-z_{1}\right)}\tilde{u}+\frac{-k^{2}}{\left(z-z_{1}\right)^{2}}\tilde{u}\left[\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}\right].</math></center> | |||
Mientras que la primera derivada longitudinal es | |||
(3.1.4)<center><math> | |||
\frac{\partial\tilde{u}}{\partial z}=\tilde{u}\left(-\frac{1}{\left(z-z_{1}\right)}\right)+\tilde{u}\left(-ik\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2\left(z-z_{1}\right)^{2}}\right),</math></center> | |||
de manera que satisface exactamente la ecuación paraxial.<math>\square</math> | |||
== | ==Ondas Gaussianas - solución acotada== | ||
Considere la solución para <math>\tilde{z}_{1}=a+ib</math> compleja, <math>x_{1},\; y_{1}=0</math>. | Considere la solución para <math>\tilde{z}_{1}=a+ib</math> compleja, <math>x_{1},\; y_{1}=0</math>. | ||
El término involucrando la dirección de propagación puede escribirse | El término involucrando la dirección de propagación puede escribirse como | ||
(4.1)<center><math> | |||
\frac{1}{\left(z-\tilde{z}_{1}\right)}=\frac{z+a}{\left(z-a\right)^{2}+b^{2}}+\frac{ib}{\left(z-a\right)^{2}+b^{2}}=\frac{1}{R}+\frac{2i}{kw^{2}}</math></center> | \frac{1}{\left(z-\tilde{z}_{1}\right)}=\frac{z+a}{\left(z-a\right)^{2}+b^{2}}+\frac{ib}{\left(z-a\right)^{2}+b^{2}}=\frac{1}{R}+\frac{2i}{kw^{2}}.</math></center> | ||
El primer término involucra la fase y se describe por el inverso de | El primer término involucra la fase y se describe por el inverso de la función radio de curvatura | ||
la función radio de curvatura<center><math> | (4.2)<center><math> | ||
R=\left(z-a\right)+\frac{b^{2}}{\left(z-a\right)} | R=\left(z-a\right)+\frac{b^{2}}{\left(z-a\right)}.</math></center> | ||
El segundo término, puesto que en la fase | El segundo término, puesto que en la fase | ||
está multiplicada por <math>ik</math>, es una amplitud decreciente en las direcciones | está multiplicada por <math>ik</math>, es una amplitud decreciente en las direcciones transversales | ||
(4.3)<center><math> | |||
\exp\left(-\frac{k}{2}\frac{\left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}}{b\left[\frac{\left(z-a\right)^{2}}{b^{2}}+1\right]}\right).</math></center> | \exp\left(-\frac{k}{2}\frac{\left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}}{b\left[\frac{\left(z-a\right)^{2}}{b^{2}}+1\right]}\right).</math></center> | ||
De manera que corresponde a una Gaussiana en ambos ejes transversales | De manera que corresponde a una Gaussiana en ambos ejes transversales | ||
<math>\exp\left(-x_{j}^{2}/w^{2}\right)</math> que decae a <math>1/e</math> a una distancia<center><math> | <math>\exp\left(-x_{j}^{2}/w^{2}\right)</math> que decae a <math>1/e</math> a una distancia | ||
(4.4)<center><math> | |||
w^{2}=b\frac{\lambda}{\pi}\left[\frac{\left(z-a\right)^{2}}{b^{2}}+1\right],</math></center> | w^{2}=b\frac{\lambda}{\pi}\left[\frac{\left(z-a\right)^{2}}{b^{2}}+1\right],</math></center> | ||
donde hemos utilizado la relación <math>k=\frac{2\pi}{\lambda}</math>. Para | donde hemos utilizado la relación <math>k=\frac{2\pi}{\lambda}</math>. Para | ||
definir el valor de las constantes ''a, b'' en términos de cantidades | definir el valor de las constantes ''a, b'' en términos de cantidades | ||
con mayor significado físico, considere el plano <math>z=a=z_{0}</math>, entonces | con mayor significado físico, considere el plano <math>z=a=z_{0}</math>, entonces | ||
<center><math> | (4.5)<center><math> | ||
w^{2}\left(z=z_{0}\right)=w_{0}^{2}=b\frac{\lambda}{\pi}\quad\Rightarrow\quad b=\frac{\pi}{\lambda}w_{0}^{2}</math></center> | w^{2}\left(z=z_{0}\right)=w_{0}^{2}=b\frac{\lambda}{\pi}\quad\Rightarrow\quad b=\frac{\pi}{\lambda}w_{0}^{2},</math></center> | ||
donde <math>w_{0}</math> es el valor mínimo de la función <math>w\left(z\right)</math> | donde <math>w_{0}</math> es el valor mínimo de la función <math>w\left(z\right)</math> y se conoce como la cintura del haz | ||
y se conoce como la cintura del haz <center><math> | (4.6)<center><math> | ||
w=w_{0}\sqrt{\frac{\left(z-a\right)^{2}}{b^{2}}+1}</math></center> | w=w_{0}\sqrt{\frac{\left(z-a\right)^{2}}{b^{2}}+1}.</math></center> | ||
Por otro lado, si se | Por otro lado, si se consideran dos planos el primero como <math>z-a=0</math> entonces <math>w\left(z-a=0\right)=w_{0}</math> y el área el haz es <math>A\left(z-a=0\right)=\pi w^{2}=\pi w_{0}^{2}=A_{0}</math>, el segundo plano como <math>z-a=b\equiv z_{R}</math>, entonces | ||
<math>w\left(z_{R}\right)=\sqrt{2}w_{0}</math> | <math>w\left(z_{R}\right)=\sqrt{2}w_{0}</math>, puesto que el área del haz es | ||
<math>\pi w^{2}</math>, | <math>A\left(z-a=z_{R}\right)=\pi w^{2}=\pi \left(\sqrt{2}w_{0}\right)^{2}=2 A_{0}</math>, i.e. la distancia <math>z_{R}</math> es aquella en la cual el área crece el doble de <math>A_{0}</math>. Ésta distancia | ||
se conoce en física como distancia de Rayleigh<center><math> | se conoce en física como distancia de Rayleigh. | ||
z_{R}=\frac{k}{2}w_{0}^{2}=\frac{\pi}{\lambda}w_{0}^{2}. | (4.7)<center><math> | ||
{z_{R}=\frac{k}{2}w_{0}^{2}=\frac{\pi}{\lambda}w_{0}^{2}}.</math></center> | |||
En el ámbito fotográfico, es una medida de la profundidad de campo | En el ámbito fotográfico, es una medida de la profundidad de campo | ||
que estima la nitidez de las imágienes en distintos planos. | que estima la nitidez de las imágienes en distintos planos. | ||
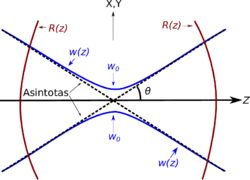
El radio del haz (donde decae a <math>1/e</math>) es entonces<center><math> | [[Archivo:ER1.svg|250px|thumb|right|'''Figura. 4.1''' Esquema del comportamiento del diámetro de un haz gaussiano y de los frentes de onda.]] | ||
w\left(z\right)=w_{0}\sqrt{\frac{\left(z-z_{0}\right)^{2}}{z_{R}^{2}}+1} | El radio del haz (donde decae a <math>1/e</math>) es entonces | ||
El radio de curvatura es<center><math> | (4.8)<center><math> | ||
R\left(z\right)=\left(z-z_{0}\right)+\frac{z_{R}^{2}}{\left(z-z_{0}\right)} | {w\left(z\right)=w_{0}\sqrt{\frac{\left(z-z_{0}\right)^{2}}{z_{R}^{2}}+1}},</math></center> | ||
La representación polar de <math>\frac{1}{\left(z-\tilde{z}_{1}\right)}=\frac{1}{R}+\frac{2i}{kw^{2}}</math> | notar que si <math>z=z_{0}</math> se obtiene que <math>w=w_{0}</math> la cual es una representación más real de un haz, pues en los experimentos no vemos que el diámetro de un haz se reduzca a un punto en <math>z=z_{0}</math>, también en el límite cuando <math>z>>z_{0}</math> obtenemos el caso asintótico (ver Figura. 4.1). | ||
\frac{1}{R}+\frac{2i}{kw^{2}}=\sqrt{\frac{1}{R^{2}}+\frac{4}{k^{2}w^{4}}}\exp\left[i\arctan\left(\frac{ | El radio de curvatura es | ||
<math>\frac{R}{w^{2}}</math> puede reescribirse como <center><math> | (4.9)<center><math> | ||
{R\left(z\right)=\left(z-z_{0}\right)+\frac{z_{R}^{2}}{\left(z-z_{0}\right)}},</math></center> | |||
para el radio de curvatura también vemos los casos límite, cuando <math>z \rightarrow z_{0}</math> y cuando <math>z \rightarrow \infty </math> el radio de curvatura diverge i.e. tiene comportamiento como onda plana. | |||
La representación polar de <math>\frac{1}{\left(z-\tilde{z}_{1}\right)}=\frac{1}{R}+\frac{2i}{kw^{2}}</math> es | |||
(4.10)<center><math> | |||
\frac{1}{R}+\frac{2i}{kw^{2}}=\sqrt{\frac{1}{R^{2}}+\frac{4}{k^{2}w^{4}}}\exp\left[i\arctan\left(\frac{2R}{kw^{2}}\right)\right],</math></center> | |||
<math>\frac{R}{w^{2}}</math> puede reescribirse como | |||
(4.11)<center><math> | |||
\frac{R}{w^{2}}=\frac{k\; z_{R}}{2\left(z-z_{0}\right)}</math></center> | \frac{R}{w^{2}}=\frac{k\; z_{R}}{2\left(z-z_{0}\right)}</math></center> | ||
y<center><math> | y | ||
\frac{1}{R^{2}}+\frac{4}{k^{2}w^{4}}=\frac{1}{\left(z-z_{0}\right)^{2}+z_{R}^{2}}=\left(\frac{w_{0}}{z_{R}w}\right)^{2}</math></center> | (4.12)<center><math> | ||
de manera que<center><math> | \frac{1}{R^{2}}+\frac{4}{k^{2}w^{4}}=\frac{1}{\left(z-z_{0}\right)^{2}+z_{R}^{2}}=\left(\frac{w_{0}}{z_{R}w}\right)^{2},</math></center> | ||
\sqrt{\frac{1}{R^{2}}+\frac{4}{k^{2}w^{4}}}\exp\left[i\arctan\left(\frac{ | de manera que | ||
mientras que la fase es<center><math> | (4.13)<center><math> | ||
ik\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2\left(z-z_{1}\right)}=ik\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2R}-\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{w^{2}}</math></center> | \sqrt{\frac{1}{R^{2}}+\frac{4}{k^{2}w^{4}}}\exp\left[i\arctan\left(\frac{2R}{kw^{2}}\right)\right]=\frac{w_{0}}{z_{R}w}\exp\left[i\arctan\left(\frac{z_{R}}{z-z_{0}}\right)\right],</math></center> | ||
mientras que la fase es | |||
(4.14)<center><math> | |||
ik\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2\left(z-z_{1}\right)}=ik\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2R}-\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{w^{2}}.</math></center> | |||
La amplitud compleja es entonces | |||
(4.15)<center><math> | |||
\tilde{u}=A_{0}\frac{w_{0}}{z_{R}w}\exp\left[i\arctan\left(\frac{z_{R}}{z-z_{0}}\right)\right] | |||
\exp\left(-\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{w^{2}}\right)\exp\left(ik\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2R}\right). | |||
</math></center> | |||
La solución de la ecuación diferencial en la aproximación paraxial es una Gaussiana dada por | |||
(4.16)<center><math> | |||
\psi=A_{0}\frac{w_{0}}{z_{R}w}\exp\left[i\arctan\left(\frac{z_{R}}{z-z_{0}}\right)\right] | |||
\exp\left(-\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{w^{2}}\right)\exp\left(ik\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2R}\right)\exp\left(ikz\right). | |||
</math></center> | |||
Gráficas de esta función se encuentran en la página de [[Ondas: Gaussianas]] | |||
---- | |||
<references/> | |||
--[[Usuario:Lazaro Palafox Maldonado|LPM]] 11:30 25 nov 2015 (CDT) | |||
--[[Usuario:Mfg|Mfg]] 16:57 1 jul 2008 (CDT) | |||
corrección | |||
--[[Usuario:Carlos A.Z.|CAZ]] 00:50 9 jul 2008 (CDT) | |||
--[[Usuario:Mfg|Mfg]] 21:48 6 ago 2008 (CDT) | |||
[[Category:optica]] | |||
[[Category:ondas]] | |||
Revisión actual - 18:26 24 ene 2023
aproximación paraxial: soluciones Gaussianas
Ecuación diferencial de onda paraxial
(1.1)
para una onda monocromática deviene en la ecuación de Helmholtz
(1.2)
donde . Considere que la onda se propaga preferencialmente en la dirección z,
(1.3)
donde es un campo complejo [1]. El gradiente es entonces
(1.4)
y el laplaciano escrito como la divergencia del gradiente es
(1.5)
pero
(1.6)
de manera que
(1.7)
La ecuación de Helmhlotz (sin aproximaciones aún) es entonces
(1.8)
La aproximación paraxial requiere que y
(1.9)
El operador nabla se puede expresar en términos de un operador transversal mas un operador longitudinal . En coordenadas cartesianas o en coordenadas cilíndricas . De manera que el laplaciano se puede sustituir por el laplaciano transversal para obtener la ecuación de onda paraxial
(1.10)
que es una ecuación parabólica.
Solución de onda esférica
Una solución exacta de la ecuación de onda son las ondas esféricas
(2.1)
Demostración: El gradiente de la magnitud radial es . De manera que
(2.2)
El laplaciano es entonces
(2.3)
pero y
(2.4)
de manera que el laplaciano deviene
(2.5)
y se satisface la ecuación de onda monocromática.
Solución aproximada de ecuación de onda
La expansión de la distancia radial en ejes cartesianos con una dirección preferencial, digamos z es
(3.1)
La solución aproximada del resultado esférico exacto es entonces
(3.2)
Si se expresa ésta ecuación en términos de la forma preferencial , se obtiene
(3.3)
Solución exacta de la ecuación paraxial
Éste resultado es la solución exacta a la ecuación diferencial aproximada.
Demostración: El gradiente transversal es
(3.1.1)
y el laplaciano transversal
(3.1.2)
que puede escribirse como
(3.1.3)
Mientras que la primera derivada longitudinal es
(3.1.4)
de manera que satisface exactamente la ecuación paraxial.
Ondas Gaussianas - solución acotada
Considere la solución para compleja, . El término involucrando la dirección de propagación puede escribirse como
(4.1)
El primer término involucra la fase y se describe por el inverso de la función radio de curvatura
(4.2)
El segundo término, puesto que en la fase está multiplicada por , es una amplitud decreciente en las direcciones transversales
(4.3)
De manera que corresponde a una Gaussiana en ambos ejes transversales que decae a a una distancia
(4.4)
donde hemos utilizado la relación . Para definir el valor de las constantes a, b en términos de cantidades con mayor significado físico, considere el plano , entonces
(4.5)
donde es el valor mínimo de la función y se conoce como la cintura del haz
(4.6)
Por otro lado, si se consideran dos planos el primero como entonces y el área el haz es , el segundo plano como , entonces , puesto que el área del haz es , i.e. la distancia es aquella en la cual el área crece el doble de . Ésta distancia se conoce en física como distancia de Rayleigh.
(4.7)
En el ámbito fotográfico, es una medida de la profundidad de campo que estima la nitidez de las imágienes en distintos planos.
El radio del haz (donde decae a ) es entonces
(4.8)
notar que si se obtiene que la cual es una representación más real de un haz, pues en los experimentos no vemos que el diámetro de un haz se reduzca a un punto en , también en el límite cuando obtenemos el caso asintótico (ver Figura. 4.1).
El radio de curvatura es
(4.9)
para el radio de curvatura también vemos los casos límite, cuando y cuando el radio de curvatura diverge i.e. tiene comportamiento como onda plana.
La representación polar de es
(4.10)
puede reescribirse como
(4.11)
y
(4.12)
de manera que
(4.13)
mientras que la fase es
(4.14)
La amplitud compleja es entonces
(4.15)
La solución de la ecuación diferencial en la aproximación paraxial es una Gaussiana dada por
(4.16)
Gráficas de esta función se encuentran en la página de Ondas: Gaussianas
- ↑ Siegman A., Lasers, University Science Books, 1986 [cap.16 p. 626]
--LPM 11:30 25 nov 2015 (CDT)
--Mfg 16:57 1 jul 2008 (CDT)
corrección
--CAZ 00:50 9 jul 2008 (CDT)
--Mfg 21:48 6 ago 2008 (CDT)






![\nabla\left[\tilde{u}\exp\left(ikz\right)\right]=\left(\nabla\tilde{u}+ik\tilde{u}\hat{e}_{z}\right)\exp\left(ikz\right),](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2c3f4b80c06a814c43f8ae340604f3a3ddeacf0c)
![\nabla^{2}\left[\tilde{u}\exp\left(ikz\right)\right]=\left[\nabla\cdot\left(\nabla\tilde{u}+ik\tilde{u}\hat{e}_{z}\right)\right]\exp\left(ikz\right)+\nabla\left[\exp\left(ikz\right)\right]\cdot\left(\nabla\tilde{u}+ik\tilde{u}\hat{e}_{z}\right),](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/31e42a8f437ab9151ad25f46c66eca43088e88c0)
![\nabla^{2}\left[\tilde{u}\exp\left(ikz\right)\right]=\left[\nabla^{2}\tilde{u}+ik\frac{\partial\tilde{u}}{\partial z}\right]\exp\left(ikz\right)+\left[ik\frac{\partial\tilde{u}}{\partial z}-k^{2}\tilde{u}\right]\exp\left(ikz\right),](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b93d34eaec7b52be0d1b57bdc759ad791089795d)
![\nabla^{2}\left[\tilde{u}\exp\left(ikz\right)\right]=\left[\nabla^{2}\tilde{u}+2ik\frac{\partial\tilde{u}}{\partial z}-k^{2}\tilde{u}\right]\exp\left(ikz\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/50fad1b556e75b30fd71652bb6ba6f849e6fcfb7)












![{\displaystyle \nabla ^{2}\psi _{esf}=\nabla \cdot \left[\left(-{\frac {1}{r}}+ik\right){\hat {\mathbf {r} }}\psi _{esf}\right]=\left(-{\frac {1}{r}}+ik\right)\psi _{esf}\nabla \cdot {\hat {\mathbf {r} }}+\nabla \left[\left(-{\frac {1}{r}}+ik\right)\psi _{esf}\right]\cdot {\hat {\mathbf {r} }},}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/adaf8bd94ea63c067299dddd8df7b7051f35384a)

![\nabla\left[\left(-\frac{1}{r}+ik\right)\psi_{esf}\right]\cdot\hat{\mathbf{r}}=\frac{1}{r^{2}}\psi_{esf}+\left(-\frac{1}{r}+ik\right)^{2}\psi_{esf},](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4f5b3a915bf747ef380ee56aba270007ca02033e)
![\nabla^{2}\psi_{esf}=\left[\frac{2}{r}\left(-\frac{1}{r}+ik\right)+\frac{2}{r^{2}}-2\frac{ik}{r}-k^{2}\right]\psi_{esf}=-k^{2}\psi_{esf},](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/9b68ef43402ff74fc32333ae259ec3b9f922b725)






![\nabla_{T}\tilde{u}=\frac{ik}{\left(z-z_{1}\right)}\tilde{u}\left[\left(x-x_{1}\right)\hat{e}_{x}+\left(y-y_{1}\right)\hat{e}_{y}\right],](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/5c244d15af3515d4831330d2b0ef6d3f297794f0)
![{\displaystyle \nabla _{T}^{2}{\tilde {u}}={\frac {ik}{\left(z-z_{1}\right)}}{\tilde {u}}\nabla _{T}\cdot \left[\left(x-x_{1}\right){\hat {e}}_{x}+\left(y-y_{1}\right){\hat {e}}_{y}\right]+\left[{\frac {ik}{\left(z-z_{1}\right)}}\nabla _{T}{\tilde {u}}\right].\left[\left(x-x_{1}\right){\hat {e}}_{x}+\left(y-y_{1}\right){\hat {e}}_{y}\right],}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ae3650ae5c87377568210f5559682b3d0b56ae7e)
![\nabla_{T}^{2}\tilde{u}=\frac{2ik}{\left(z-z_{1}\right)}\tilde{u}+\frac{-k^{2}}{\left(z-z_{1}\right)^{2}}\tilde{u}\left[\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}\right].](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/a56a95744b3ce95544686bb2fc1301716f515543)






![\exp\left(-\frac{k}{2}\frac{\left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}}{b\left[\frac{\left(z-a\right)^{2}}{b^{2}}+1\right]}\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3c87490eb3f4760b0c241e701795f75f5c33e458)


![w^{2}=b\frac{\lambda}{\pi}\left[\frac{\left(z-a\right)^{2}}{b^{2}}+1\right],](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c040188a2a7ae81c2eb9b162b3eb3e5c9fe3a9cb)























![\frac{1}{R}+\frac{2i}{kw^{2}}=\sqrt{\frac{1}{R^{2}}+\frac{4}{k^{2}w^{4}}}\exp\left[i\arctan\left(\frac{2R}{kw^{2}}\right)\right],](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c4a559097b8235dd3110d204c510ac7ffebf6d62)



![\sqrt{\frac{1}{R^{2}}+\frac{4}{k^{2}w^{4}}}\exp\left[i\arctan\left(\frac{2R}{kw^{2}}\right)\right]=\frac{w_{0}}{z_{R}w}\exp\left[i\arctan\left(\frac{z_{R}}{z-z_{0}}\right)\right],](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d2214d2ba8b8c489df222bbf07c3bb0090827ebb)

![\tilde{u}=A_{0}\frac{w_{0}}{z_{R}w}\exp\left[i\arctan\left(\frac{z_{R}}{z-z_{0}}\right)\right]
\exp\left(-\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{w^{2}}\right)\exp\left(ik\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2R}\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d6549678113b515ff4af6f9a85ceed8fd67c8af0)
![\psi=A_{0}\frac{w_{0}}{z_{R}w}\exp\left[i\arctan\left(\frac{z_{R}}{z-z_{0}}\right)\right]
\exp\left(-\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{w^{2}}\right)\exp\left(ik\frac{\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}}{2R}\right)\exp\left(ikz\right).](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/76dd4db3d6a49e2709aecf354596a3ee8f07df08)