Optica: Integral de Kirchhoff - Fresnel

Principio de Huygens-Fresnel

La idea básica de la teoría de Huygens-Fresnel es que la perturbación luminosa en un punto P en el espacio, surge de la superposición de ondas esféricas secundarias originadas en cada punto del frente de una onda primaria situada entre P y la fuente.

Fuentes Ficticias

Sin embargo, no existe evidencia física de fuentes luminosas sobre cada punto de la superficie de un frente de onda, por lo que el principio de Huygens es simplemente una suposición que conduce a una descripción bastante buena de algunos fenómenos de difracción; todos aquellos fenómenos conocidos como "difracción de Fresnel".

Un enfoque mas natural y preciso fue el que realizó Gustav Kirchhoff al calcular la solución de la ecuación de onda electromagnética escalar en un punto P en el espacio, en términos de su solución y gradiente, evaluados sobre una superficie cerrada arbitraria S que rodea a P. Este es el conocido teorema integral de Kirchhoff. Cabe mencionar que Helmholtz derivó previamente este teorema de sus estudios en acústica para ondas monocromáticas.

Teorema Integral de Helmholtz-Kirchhoff

Desarrollo matemático

Nuestro estudio se limitará a ondas electromagnéticas monocromáticas en el vacio. Sea $E$ la onda incidente, que obedece a la ecuación diferencial escalar:

$\nabla ^{2}E={\frac {1}{c^{2}}}{\frac {\partial ^{2}E}{\partial t^{2}}}$ (1)

Apliquemos el método de separación de variables para resolver esta ecuación. Sea $E(x,y,z,t)=U(x,y,z)e^{-i\omega t}$ nuestra función separable en una función $U$, que solo depende de las coordenadas $x,y,z$ y otra dependiente únicamente del tiempo. Al sustituirla en (1) se obtienen dos ecuaciones diferenciales, una de las cuales, la que nos interesa resolver, es la ecuación de Helmholtz:

$\nabla ^{2}U+k^{2}U=0$(2)

la cual nos muetra la variación espacial de la función indeterminada $U$. $k=\omega /c$.

Para su solución nos apoyamos en el teorema de Green. Sea $V$ el volumen limitado por la superficie cerrada $S$ y sea $P$ cualquier punto dentro de $V$ ; asumimos que $U$ posee derivadas parciales de primero y segundo orden, continuas, dentro y sobre la superficie. Sea U' cualquier otra función que cumple con las mismas condiciones de continuidad que $U$. Entonces, por teorema de Green, tenemos que:

$\iiint \limits _{V}(U\nabla ^{2}U'-U'\nabla ^{2}U)\,dV=-\iint \limits _{S}(U{\overrightarrow {\nabla }}U'-U'{\overrightarrow {\nabla }}U)\cdot {\widehat {n}}dS$(3)

donde tomamos el vector ${\widehat {n}}$, normal a $S$, hacia dentro de esta.

Superficie de integración

En particular, si U' satisface también la ecuación de Helmholtz, (2), el integrando en el miembro izquierdo de (3) se hace cero en cada punto de $V$ ; y el teorema de Green se reduce a:

$\iint \limits _{S}(U{\overrightarrow {\nabla }}U'-U'{\overrightarrow {\nabla }}U)\cdot {\widehat {n}}dS=0$(4)

Ahora, se propone: $U'(x,y,z)={\frac {e^{ikr}}{r}}$

donde $r$ denota la distancia desde el punto $P$ al punto (x,y,z).

U' , expresada en esta forma, tiene una singularidad en r = 0; y como se asumió que debe ser continua y diferenciable, $P$ debe ser excluido del dominio de integración; para tal efecto lo encerraremos en una pequeña esfera hueca de radio $\epsilon$ centrada en el punto $P$ mismo. La integral (4) será evaluada, entonces, en el volumen comprendido entre $S$ y la superficie $S'$ de la pequeña esfera, como lo muestra la figura; y en lugar de (4) tenemos la siguiente integral:

$\left[\iint \limits _{S}+\iint \limits _{S'}\right](U{\overrightarrow {\nabla }}{\frac {e^{ikr}}{r}}-{\frac {e^{ikr}}{r}}{\overrightarrow {\nabla }}U)\cdot {\widehat {n}}dS=0$(5)

Ahora desarrollaremos la integral sobre la superficie $S'$.

Nos damos cuenta que:

${\overrightarrow {\nabla }}{\frac {e^{ikr}}{r}}\cdot {\widehat {n}}=\left(ik-{\frac {1}{r}}\right){\frac {e^{ikr}}{r}}$

${\overrightarrow {\nabla }}U\cdot {\widehat {n}}={\frac {\partial }{\partial r}}U$

Sustituyendo estas expresiones en (5) se obtiene lo siguiente:

$\iint \limits _{S}(U{\overrightarrow {\nabla }}{\frac {e^{ikr}}{r}}-{\frac {e^{ikr}}{r}}{\overrightarrow {\nabla }}U)\cdot {\widehat {n}}dS=-\iint \limits _{S'}\left[U\left(ik-{\frac {1}{\epsilon }}\right){\frac {e^{ik\epsilon }}{\epsilon }}-{\frac {e^{ik\epsilon }}{\epsilon }}{\frac {\partial }{\partial \epsilon }}U\right]\epsilon ^{2}d\Omega$

donde también hemos sustituido a r por $\epsilon$ y a dS' por el elemento de ángulo sólido $\epsilon ^{2}d\Omega$.

Puesto que, la integral sobre S no depende de $\epsilon$, podemos reemplazar la integral de la derecha por su valor límite cuando $\epsilon$ $\rightarrow$ 0; el primero y el tercer término se hacen cero en el proceso límite y la contribución total del segundo término es $4\pi U(P)$. Por lo tanto:

$U(P)={\frac {1}{4\pi }}\iint \limits _{S}(U{\overrightarrow {\nabla }}{\frac {e^{ikr}}{r}}-{\frac {e^{ikr}}{r}}{\overrightarrow {\nabla }}U)\cdot {\widehat {n}}dS$

que es el conocido teorema integral de Helmholtz-Kirchhoff.

Teoría de la Difracción de Kirchhoff

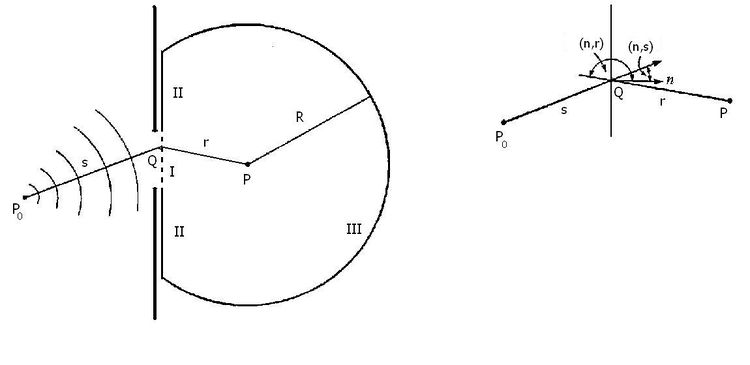
Apliquemos el teorema al problema de una onda esférica monocromática que incide sobre una abertura, en una pantalla plana y opaca. Sea el punto $P_{0}$ el origen de la onda incidente y el punto $P$ el lugar donde la perturbación será determinada. Nos aseguramos de que el ancho de la abertura sea mucho mayor que la longitud de onda $\lambda$ y mucho menor que las distancias de $P_{0}$ y $P$ a la pantalla.

Figura 2. Ilustrando la derivación de la integral de Kirchhoff- fresnel

Para encontrar la perturbación en el punto $P$ la estrategia será dividir la superficie cerrada S en tres partes. La parte I, que es igual al área de la abertura; la parte II, que es un disco sin la parte I; la parte III, que es un casquete esférico de radio $R$ centrado en $P$.

Para este problema, la integral de Kirchhoff es:

$U(P)={\frac {1}{4\pi }}\left[\iint \limits _{I}+\iint \limits _{II}+\iint \limits _{III}\right](U{\overrightarrow {\nabla }}{\frac {e^{ikr}}{r}}-{\frac {e^{ikr}}{r}}{\overrightarrow {\nabla }}U)\cdot {\widehat {n}}dS$

La dificultad emergente es que los valores de la onda incidente $U$ y su gradiente, sobre las superficies I,II y III, nunca son conocidos exactamente. Sin embargo es razonable suponer que, en cualquier parte de I, excepto en las vecindades inmediatas de los bordes de la abertura, los valores de $U$ y ∇U no difieren mucho de aquellos en ausencia de la pantalla; y que en la parte II, estas cantidades serán aproximadamente cero.

A partir de estas consideraciones, Kirchhoff estableció las siguientes condiciones en la frontera, las cuales son la base para su teoría de la difracción:

Sobre I:

$U=U^{(i)}\qquad ;\qquad \nabla U=\nabla U^{(i)}$

sobre II:

$U=0\qquad ;\qquad \nabla U=0$

donde :

$U^{(i)}=A{\frac {e^{iks}}{s}}$

es la onda incidente, y:

$\nabla U^{(i)}=\left(ik-{\frac {1}{s}}\right){\frac {Ae^{iks}}{s}}\cos {({\hat {n}},{\hat {s}})}$

La contribución de la superficie III en el punto $P$ tiende a cero para $R$ muy grande, siempre y cuando $U$ decaiga tan rapido como una onda esférica. Por lo tanto, la perturbación en el punto $P$ está dada por:

$U(P)={\frac {A}{4\pi }}\iint \limits _{I}\left\{{\frac {e^{iks}}{s}}\left(ik-{\frac {1}{r}}\right){\frac {e^{ikr}}{r}}\cos {({\hat {n}},{\hat {r}})}-{\frac {e^{iks}}{r}}\left(ik-{\frac {1}{s}}\right){\frac {e^{ikr}}{s}}\cos {({\hat {n}},{\hat {s}})}\right\}dS$

Dado que $s$ y $r$ son mucho mayores que $\lambda$, los terminos que van como $s^{2}$ y $r^{2}$ se desprecian, obteniendose así la fórmula de la difracción de Fresnel-Kirchhoff:

$U(P)=-{\frac {iA}{2\lambda }}\iint \limits _{I}{\frac {e^{ik(s+r)}}{sr}}\left[\cos {({\hat {n}},{\hat {s}})}-\cos {({\hat {n}},{\hat {r}})}\right]dS$