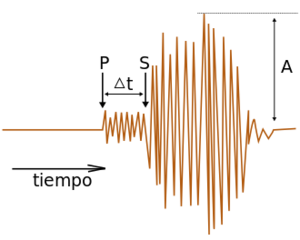Ondas sismicas
Sismología
La Sismología es la ciencia que estudia los aspectos relacionados con la recurrencia de temblores de tierra, terremotos o sismos, es decir, a través de estos, su distribución espacio temporal, mecanismos en el foco y liberación de energía, pone de manifiesto los procesos dinámicos que están sucediendo en la Tierra. Asimismo, el estudio de la propagación de las ondas producidas por los terremotos nos da información sobre su estructura interior, las regiones que la forman y la distribución de la densidad y de las constantes elásticas que presenta.
La propagación de las ondas producidas por los terremotos está determinada por la mecánica de los medios elásticos y, por tanto, sus velocidades dependen de las características elásticas del medio, cuya distribución puede estudiarse mediante la observación de los tiempos de recorrido y amplitudes de estas ondas. Las soluciones obtenidas para las ondas elásticas representan dos tipos de ondas (llamadas internas o de volumen) que se propagan con distinta velocidad. Las de mayor velocidad, y por tanto las primeras en llegar, son las llamadas ondas P, que corresponden a ondas longitudinales. Las segundas en aparecer, debido a su menor velocidad, son las ondas S, que tienen carácter transversal.
El estudio de estas ondas se realiza mediante las relaciónes de reflexión y refracción, ya que la Tierra está formada por capas de distinto material. Sus trayectorias y tiempos de llegada se determinan, bien considerando capas planas, cada una de velocidad constante o aumentando con la profundidad[1].
Las ondas y el medio elástico
Una onda recibe el nombre de onda elástica cuando una perturbación se propaga a lo largo de un medio elástico. El medio elástico se deforma y se recupera vibrando al paso de la onda. La perturbación comunica una agitación a la primera partícula del medio en que impacta, a este se le denomina como el foco de las ondas y en esa partícula se inicia la onda.
La perturbación se transmite en todas las direcciones por las que se extiende el medio que rodea al foco con una velocidad constante en todas las direcciones, siempre que el medio sea isótropo (de iguales características físico- químicas en todas las direcciones). Todas las partículas del medio son alcanzadas con un cierto retraso respecto a la primera y se ponen a vibra. El movimiento de cada partícula respecto a la posición de equilibrio en que estaba antes de llegarle la perturbación es un movimiento vibratorio armónico simple. Una onda transporta energía y cantidad de movimiento pero no transporta materia. Las partículas vibran alrededor de la posición de equilibrio, pero no viajan con la perturbación.
Origen de los terremotos o sismos
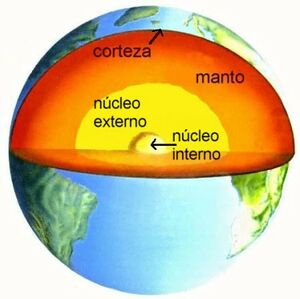
Gracias a la sismología se tiene el conocimiento de la estructura interna de la tierra, los cuales son importantes recordar para entender a los terremotos. De forma simplificada, el planeta esta conformado por un núcleo, hecho principalmente de metales como el hierro y níquel; después, está el manto, compuesto de silicatos a base de sodio, calcio y potasio; por último, se tiene a la corteza terrestre, que es la capa de roca más externa de la tierra.
La corteza terrestre y parte exterior del manto puede considerarse como un cuerpo rígido "flotando" en el resto del manto en donde pueden ocurrir movimientos como si se tratara de un fluido. Sin embargo, la semejanza a la naturaleza de un fluido solo es correcta cuando se consideran tiempos muy extensos (tiempos geológicos).
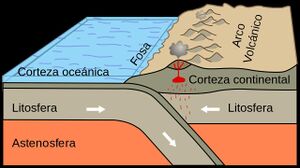
La litosfera (el cascarón exterior del planeta) está conformado por varias "placas" que hacen contacto entre sí, lo cual hace que esta parte de la tierra no sea continua sobre su superficie. Las placas presentan movimiento relativo entre ellas gracias a que, a lo largo de estas, se aplican fuerzas generadas por las corrientes de convección dentro del planeta. Este movimiento relativo ocurre cuando surge más litosfera en los margenes de las placas o cuando las placas se enciman unas con otras (esto último se conoce como subducción).
Las corrientes de convección se manifiestan normalmente en fluidos como el agua, pero hay que recordar que parte de la tierra puede ser considerada como un fluido si se toman tiempos extensos.
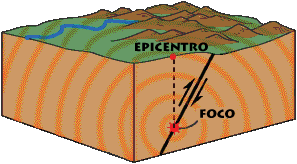
Claramente las placas no son lisas; cuando dos de ellas entran en contacto tratan de detenerse mutuamente con las fuerzas de fricción, pero a medida que la fuerza de tensión aumenta se libera el movimiento. Este movimiento no es continuo; las placas tratarán de detenerse en todo su trayecto y las fuerzas de tensión aumentarán haciendo que vuelvan a moverse. La liberación repentina de esfuerzos impuestos al terreno genera los temblores alrededor de la región. Los planos de deslizamiento entre placas se llaman fallas y el lugar donde se inició el choque provocando el temblor se llama foco; la proyección de este último en la superficie terrestre se llama epicentro. [2]
La zona donde se tocan las placas se llama zona de Wadati-Benioff.
Ondas internas
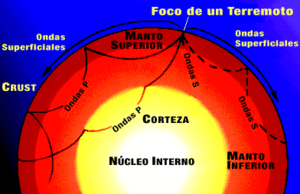
Las ondas internas son las que se transmiten en el interior de la tierra. Estas ondas se estudian como las que se propagan en cuerpos sólidos (ya que esta zona de la tierra es considerado como un sólido elástico). Se pueden transmitir de dos maneras: a través de ondas P u ondas S. Las diferencias de densidad en distintas zonas de la tierra provoca que la trayectoria de estas ondas sigan curvas a través de su interior (No son lineales).
Este tipo de ondas pueden llegar a la superficie provocando las ondas superficiales.[2]
Ondas P
También conocidas como ondas primarias, se pueden propagar en materiales sólidos y líquidos. Estas ondas son las que causan menos daño en un terremoto debido a que son ondas del tipo longitudinal, las cuales se transmiten a través de perturbaciones y rarefacciones, es decir, las partículas del medio se mueven en la dirección en la que se propaga la onda, esto ocasiona que la roca del suelo se compacte y estire en dirección del movimiento de la onda, sin embargo, una vez que pasa la onda el material, en este caso el suelo, vuelve a su estado original. Las ondas P se caracterizan por su velocidad ya que son 1.7 más rápidas que las ondas S; su velocidad a través de un medio esta dada por:
\[ v_{p} = \sqrt{{k + {3 \over 4}{\mu}} \over \rho} \]
$\bullet$ $v_{p}$ es la velocidad de la onda P.
$\bullet$ $k$ es el módulo de compresibilidad, el cual es un número que indica que tanto se reduce el volumen del medio al ser sometido a una presión o comprensión determinada. [3]
$\bullet$ $\mu$ es el módulo de rigidez, el cual es un número que expresa la resistencia del medio de ser deformado.
$\bullet$ $\rho$ es la densidad del medio.
En el caso de las ondas sísmicas, la roca de la tierra es la que sufre las comprensiones y rarefacciones.[2]
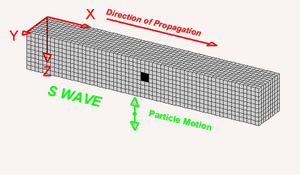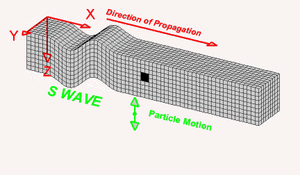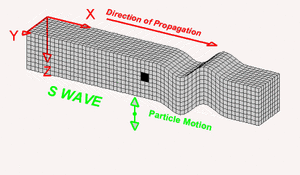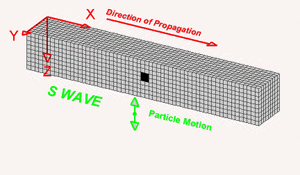
Ondas S
Las ondas S tambien conocidas como Secundarias son ondas transversales o de corte, lo cual significa que el suelo es desplazado perpendicularmente a la dirección de propagación, alternadamente hacia un lado y hacia el otro, esta característica hace que cause más daño en un terremoto en comparación a una onda P, y, al tener mayor amplitud que la P se tendrá una sensación más fuerte durante un temblor. Las ondas S pueden viajar únicamente a través de sólidos debido a que los líquidos no pueden soportar esfuerzos de corte. Su velocidad es alrededor de 58% la de una onda P para cualquier material sólido, esta onda es más lenta debido a su movimiento transvesal. Su velocidad está dada por:
\[ v_{s} = \sqrt{{\mu} \over \rho} \]
Las variables tienen el mismo significado que en las ondas P. Para las ondas sísmicas, el movimiento transversal lo realiza la sección de roca a la que le llega la perturbación, es decir, la roca se moverá de arriba a abajo o de lado a lado.[2]
Radiación de las ondas de un terremoto
El momento sísmico $M$ de un terremoto es la cantidad de energía liberada por este. Con ayuda de su derivada la radiación de un terremoto en el campo lejano provocado por una falla se puede describir de la siguiente manera:
Ondas P
$u^{P}(t)={1 \over {{4}{\pi}{}\rho_{0}}{{\alpha^{3}}_{0}}}{\sqrt{{{\rho_{0}}{\alpha_{0}}} \over {{\rho}{\alpha}{J}}}}{R^{P}(\gamma)}{\dot{M}(t-T_{\alpha})}$
Ondas S
$u^{S}(t)={1 \over {{4}{\pi}{}\rho_{0}}{{\beta^{3}}_{0}}}{\sqrt{{{\rho_{0}}{\beta_{0}}} \over {{\rho}{\beta}{J}}}}{R^{S}(\gamma)}{\dot{M}(t-T_{\beta})}$
Donde $\rho$, $\alpha$, $\beta$ son la densidad y la velocidad de las ondas P y S en la tierra, respectivamente. El subindice 0 significa que esos valores fueron medidos en la fuente del terremoto. $J$ es la divergencia geométrica que mide la variación de amplitudes debida a la dilatación espacial de los frentes de onda. El tiempo de propagación es $T_{\alpha}$ o $T_{\beta}$ para las ondas P o S, respectivamente. $R^{P}(\gamma)$ y $R^{S}(\gamma)$ representan diagramas de radiación cuadrupolar de las ondas P y S, respectivamente. ${\gamma}$ es un vector unitario en dirección a la propagación. El término ${\dot{M}(t-T)}$ es la derivada del momento sísmico, la cual es la señal producida por la fuente y que se propaga con la velocidad de las ondas P o s a lo largo de los rayos sísmicos.
Muchos científicos como Raúl Madariaga[4] han demostrado que para cualquier modelo de falla:
\[ \omega_{0}=N{\beta \over L} \]
Donde $N$ es un factor numérico vecino de 2.3 y ${\beta}$ es la velocidad de las ondas S.[4]
Ecuación de movimiento y ecuación de onda
La ecuación de movimiento de un cuerpo fué planteada por Lamé-Navier y esta está en función de los desplazamientos para un medio continuo, elástico, lineal, isótropo y homogéneo: \begin{equation} (\lambda\ +\mu\ )\nabla (\nabla \cdot u)+ \mu \nabla^2 (\nabla \cdot u) + F = \rho u \label{1} \end{equation}
Donde el primer y segundo término son el gradiente de la divergencia y el Laplaciano de los desplazamientos y F son las fuerzas internas y externas. Recurriendo a la identidad matemática:
\begin{equation} \nabla^2 u=\nabla (\nabla \cdot u)-(\nabla \times \nabla \times u) \label{2} \end{equation}
se obtiene: \begin{equation} \rho u = (\lambda\ +2\mu\ )\nabla (\nabla \cdot u)-(\mu\nabla\times\nabla\times u) \label{3} \end{equation}
Utilizando el teorema de Helmholtz para el campo de desplazamientos:
\begin{equation} u=\nabla \phi + \nabla\times\psi \label{4} \end{equation}
Donde, $\phi$ es el potencial escalar $ \nabla\times\phi=0$ irrotacional y $\psi$ es el potencial vectorial $(\nabla\cdot\psi=0)$,sin cambio volumétrico. Al reemplazar las expresiones anteriores en la ecuación de movimiento, y usando $(\nabla\times\nabla\times\phi=-\nabla^2\psi, para \nabla\cdot\psi=0)$: Esto se cumple en la medida que ambos términos son nulos.
Definiendo entonces: \begin{equation} \alpha=\sqrt{\frac{\lambda +2\mu}{\rho}} \label{5} \end{equation} \begin{equation} \beta=\sqrt{\frac{\mu}{\rho}} \label{6} \end{equation}
obteniendo:
\begin{equation}
\nabla^2\phi - \frac{1}{\alpha^2} \ddot{\phi}=0
\label{7}
\end{equation}
\begin{equation}
\nabla^2\psi - \frac{1}{\beta^2} \ddot{\psi}=0
\label{8}
\end{equation}
Así, existe una ecuación de onda escalar para $\phi$y una onda vectorial para $\tilde{\psi}$;La ecuación escalar está asociada a la onda P y la vectorial a la onda S. Luego, α es la velocidad de la onda compresional P, mientras β es la velocidad de la onda de corte S. Así, podemos obtener los desplazamientos como: \begin{equation} u=\nabla\phi+\nabla\times\vec \psi \label{9} \end{equation}
\begin{equation} \vec \psi=(\psi_1,\psi_2,\psi_3) \label{10} \end{equation}
Al separar estas expresiones por componentes, se tienen los desplazamientos en función de los potenciales, obteniendo: \begin{equation} u_1 = \frac{\partial \phi}{\partial x_1} + \frac{\partial \psi_3}{\partial x_2} + \frac{\partial \psi_2}{\partial x_3} \label{11} \end{equation}
:
\begin{equation}
u_2 = \frac{\partial \phi}{\partial x_2} + \frac{\partial \psi_3}{\partial x_1} + \frac{\partial \psi_1}{\partial x_3}
\label{12}
\end{equation}
:
\begin{equation}
u_2 = \frac{\partial \phi}{\partial x_2} + \frac{\partial \psi_2}{\partial x_1} + \frac{\partial \psi_1}{\partial x_2}
label{13}
\end{equation}
Consideremos las ecuaciones de movimiento (2) y campo de desplazamiento (3). y ecuaciones con desplazamiento: \begin{equation} \nabla\lfloor (\lambda+2\mu)\nabla^2\phi-\rho\ddot\phi\rfloor + \nabla\times\lfloor \mu\nabla^2\psi-\rho\psi\rfloor = 0 \label{14} \end{equation}
Los desplazamientos debidos a la onda P en coordenadas cartesianas son: \begin{equation} U_p=\nabla\phi=\frac{\partial\phi}{\partial x_1}\hat x_1+\frac{\partial\phi}{\partial x_2}\hat x_2+\frac{\partial\phi}{\partial x_3}\hat x_3 \label{15} \end{equation}
Es importante destacar que $\phi$ satisface: \begin{equation} \frac{\partial^2 \phi}{\partial t^2}=\alpha^2\cdot (\frac{\partial^2 \phi}{\partial x_1 ^2} + \frac{\partial^2 \phi}{\partial x_2 ^2} + \frac{\partial^2 \phi}{\partial x_3 ^2}) \label{16} \end{equation}
Para resolverla, buscamos una solución con separación de variables del tipo: \begin{equation} \phi (x_1, x_2, x_3, t)=X(x_1)Y(x_2)Z(x_3)T(t) \label{17} \end{equation}
Reemplazando y dividiendo ambos lados por XYZT, se obtiene: \begin{equation} \frac{\partial^2 T}{\partial t ^2}\cdot\frac{1}{T} = \alpha^2\cdot (\frac{\partial^2 X}{\partial x_1 ^2}\cdot\frac{1}{X} + \frac{\partial^2 Y}{\partial x_2 ^2}\cdot\frac{1}{Y} + \frac{\partial^2 Z}{\partial x_1 ^2}\cdot\frac{1}{Z}) \label{18} \end{equation}
Al igual que para una variable espacial, se asume que si la solución satisface la ecuación, cada término es una constante:
\begin{equation} \alpha^2\cdot\frac{\partial^2 X}{\partial x_1^2}\cdot\frac{1}{X}=k_1 ^2; \alpha^2\cdot\frac{\partial^2 Y}{\partial x_2^2}\cdot\frac{1}{Y}=k_2 ^2; \alpha^2\cdot\frac{\partial^2 Z}{\partial x_3^2}\cdot\frac{1}{Z}=k_3 ^2 \label{19} \end{equation}
De (19) se deduce que:
\begin{equation} \ddot T +\omega^2 T=0 <br>: \ddot X + k_1 ^2 X=0 <br>:\ddot y + k_2 ^2 Y=0 <br>: \ddot Z + k_3 ^2 X=0 \label{20} \end{equation}
Concluyendo que: \begin{equation} k_1 ^2 +k_2 ^2 +k_3 ^2 = \frac{\omega^2}{\alpha^2} \label{21} \end{equation}
Asumiendo soluciones armónicas, de acuerdo a la definición de la solución propuesta, se tiene: \begin{equation} \phi (x,t)=AeExp\pm i(\omega(\pm k_1 x_1 \pm k_2 x_2 \pm k_3 x_3) \label{22} \end{equation}
Esta ecuación indica una dependencia espacio temporal del potencial, donde el argumento del exponencial es la fase. Una onda de frecuencia ω y velocidad α, que cumpla con: \begin{equation} k_1 ^2 +k_2 ^2 +k_3 ^2 =\frac{\omega^2}{\alpha^2}=cte \label{23} \end{equation}
define una superficie plana en el sistema cartesiano con vector normal: \begin{equation} k_\alpha = |k_\alpha|\hat k=(\frac{\omega^2}{\alpha^2})\hat k \label{24} \end{equation}
Este vector define la dirección de propagación de la onda, normal a la onda plana. Una forma alternativa de escribir la ecuación anterior está dada por: \begin{equation} \phi(x,t)=AeExp(i(\omega t - k_\alpha x)) \label{25} \end{equation}
Los desplazamientos asociados a la onda S están dados por la ecuación: \begin{equation} U_S =\nabla\times\psi \label{26} \end{equation}
Correspondiente a la solución de la ecuación vectorial: \begin{equation} \frac{\partial^2 \psi}{\partial t^2}=\beta^2(\frac{\partial^2 \psi}{\partial x_1 ^2} + \frac{\partial^2 \psi}{\partial x_2 ^2} + \frac{\partial^2 \psi}{\partial x_3 ^2}) \label{27} \end{equation}
Esta solución estará dada por: \begin{equation} \psi(x,t)=BeExp(i(\omega t - k_\beta x)) \label{28} \end{equation}
Donde: \begin{equation} k_\beta =(\frac{\omega}{\beta}) \label{29} \end{equation}
Si se considera una onda propagándose según un vector número de onda $k_\beta$, en el plano $x_1 y x_3$, se tiene que:
\begin{equation} \frac{\partial \phi}{\partial x_2}=0 ; k_2=0 \label{30} \end{equation}
Asumiendo que la fase es constante, tenemos que:
\begin{equation} \omega t - k_1 x_1 - k_3 x_3 =C \label{31} \end{equation}
De esta expresión se deduce que el vector número de onda es perpendicular al plano de la onda, con componentes $k_1$ y $k_3$en los ejes $x_1$ y $x_3$.
El término de la fase:$\omega t - k_1 x_1 - k_3 x_3 $Corresponde a una onda que se propaga en la dirección $+x_1$ y $+x_3$. Esto implica que:
\begin{equation}
U_p =\nabla\phi=\frac{\partial \phi}{\partial x_1}\hat x_1 +\frac{\partial \phi}{\partial x_2}\hat x_2 +\frac{\partial \phi}{\partial x_3}\hat x_3
\label{32}
\end{equation}
:
\begin{equation}
U_s =(\frac{\partial \psi_3}{\partial x_2}-\frac{\partial \psi_2}{\partial x_3})\hat x_1 +(\frac{\partial \psi_3}{\partial x_1}-\frac{\partial \psi_1}{\partial x_3})\hat x_2 + (\frac{\partial \psi_2}{\partial x_1}-\frac{\partial \psi_1}{\partial x_2})\hat x_3
\label{33}
\end{equation}
Asumiendo que una onda P tiene el siguiente potencial asociado: \begin{equation} \phi = AeExp(i(\omega t-k_1 x_1 - k_3 x_3)) \label{34} \end{equation}
Se tiene una expresión para los desplazamientos de la forma: \begin{equation} U_p=\frac{\partial \phi}{\partial x_1}\hat x_1 +\frac{\partial \phi}{\partial x_2}\hat x_2 +\frac{\partial \phi}{\partial x_3}\hat x_3 \label{35} \end{equation}
\begin{equation} U_p(x,t)=(-iK_1A)eExp(i(\omega t-k_1 x_1 - k_3 x_3))\hat x_1 + 0\hat x_2 +(-iK_3A)eExp(i(\omega t-k_1 x_1 - k_3 x_3))\hat x_3 \label{36} \end{equation}
Tomando la razón entre el movimiento vertical y el horizontal se tiene que: \begin{equation} \frac{U_p\,_3}{U_p\,_1}=\frac{k_3}{k_1} \label{37} \end{equation}
Lo que define un plano perpendicular al frente de onda y paralelo a la dirección depropagación, de manera que la partícula avanza y retrocede en la línea de propagación, comprimiendo y dilatando el medio. De la misma forma, la onda S tiene sus desplazamientos dados por: \begin{equation} U_s=(\frac{\partial \psi_3}{\partial x_2}-\frac{\partial \psi_2}{\partial x_3})\hat x_1 +(\frac{\partial \psi_3}{\partial x_1}- \frac{\partial \psi_1}{\partial x_3})\hat x_2 + (\frac{\partial \psi_2}{\partial x_1}-\frac{\partial \psi_1}{\partial x_2})\hat x_3 \label{38} \end{equation}
En el plano $x_1 x_3$ tendremos:
\begin{equation} \frac{\partial \phi}{\partial x_2} = 0: k_2 = 0 \label{39} \end{equation}
De las ecuaciones se deduce un movimiento en la vertical y horizontal en el plano $ x_1 x_3$, y además, un movimiento horizontal en $x_2$. $U_s\,_1$ y $U_s\,_3$> se denominan componente SV de la onda S, que generan movimiento vertical en el plano x1x3, mientras que la componente US3 se denomina componente SH de la onda S, ya que es puramente horizontal. Finalmente, el desplazamiento total, asociado al desplazamiento de las ondas P, SV y SH, está dado por la composición de los desplazamientos:
\begin{equation} U_p + U_s=\begin{pmatrix} u_1 \\u_2\\ u_3\end{pmatrix}=\begin{pmatrix} \frac{\partial \phi}{\partial x_1}- \frac{\partial \psi_2}{\partial x_3}\\\frac{-\partial \psi_3}{\partial x_1} + \frac{\partial \psi_1}{\partial x_3}\\\frac{\partial \phi}{\partial x_3}+ \frac{\partial \psi_2}{\partial x_1}\end{pmatrix} \label{40} \end{equation}
La componente SH es absolutamente independiente de las componentes P-SV, y mientras no existan condiciones de borde o superficie libre, esta independencia se conserva.[5]
Ondas superficiales
En la superficie libre de la Tierra y en otras discontinuidades de la corteza, se producen otro tipo de ondas que por propagarse a lo largo de estas superficies reciben el nombre de ondas superficiales. Estas ondas se propagan con velocidades inferiores a las de la onda S y su amplitud decrece con la profundidad. De estas ondas existen dos tipos: unas son las llamadas ondas Rayleigh, de movimiento vertical, y otras, las ondas Love, de movimiento horizontal, nombres que corresponden a los dos científicos ingleses del siglo XIX.
En su origen, las primeras determinaciones del punto donde se produce el terremoto (foco o hipocentro) y su proyección sobre la superficie (epicentro) se basan en el estudio de la distribución de los daños producidos en los edificios, en el terreno o en las personas, y sitúan el epicentro en la zona de mayor daño (epicentro macrosísmico). Admitido el carácter puntual del foco sísmico, la localización de un terremoto viene definida por cuatro parámetros: hora, origen, coordenadas geográficas del epicentro y profundidad del foco. El primer modelo mecánico que definiese el origen de los terremotos fue propuesto por H.F. Reid en 1911 con la teoría del rebote elástico, según la cual las deformaciones elásticas se van acumulando hasta que se supera la resistencia del material, produciéndose una fractura y una liberalización de las deformaciones acumuladas.
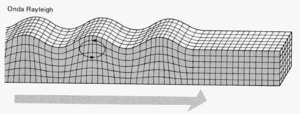
Ondas de Rayleigh
La existencia de las ondas de Rayleigh se predijo en 1885 por Lord Rayleigh quien a su vez diseñó matemáticamente el movimiento de ondas planas en un espacio seminfinito elástico.
Los terremotos también producen ondas superficiales que pueden causar un movimiento perpendicular o paralelo a la superficie. Las ondas que mueven la superficie arriba y abajo se llaman ondas de Rayleigh y se describe a veces como "rodillo de tierra". Estas son las causantes del movimiento de la superficie del suelo (hacia arriba y hacia abajo), se propagan a aproximadamente 90% de la velocidad de las ondas S [6].
En las ondas de Rayleigh son ondas elípticas, generadas por el acoplamiento en la superficie de las ondas Sy P. Los desplazamientos están restringidos entre una o dos longitudes de onda Rayleigh de la superficie. El mecanismo de propagación es complejo ya que las trayectorias de los desplazamientos de partículas en la superficie son elipses. Las ondas de Rayleigh pueden acoplarse con un medio que rodea la superficie del cuerpo, tanto líquido como aire, lo que afecta la amplitud y la velocidad de la onda. La amplitud de onda disminuye rápidamente con la profundidad y la tasa de disminución depende de la longitud de onda. Cuando hay defectos en la superficie sobre la que se propagan las ondas de Rayleigh, las ondas se dispersan, al igual que las ondas longitudinales y transversales que se propagan en la profundidad del medio [7]
Ondas de Love
Son el resultado de muchas ondas S que subieron a la superficie e interfirieron entre sí. Estas ondas son las causantes del movimiento lateral del suelo durante los terremotos; la suma de las ondas S dan movimientos periódicos hacia arriba y abajo, pero también de derecha a izquierda. Son más lentas que las ondas S y P pero más rápidas que las ondas de Rayleigh. Su amplitud y fuerza va bajando conforme a la profundidad de la zona en la que se estudia, en concreto disminuye en la razón:
\[ 1 \over \sqrt{r} \]
Donde $r$ representa la distancia que hay desde el el origen del terremoto hasta punto que la onda ha recorrido. A pesar de esta pérdida de fuerza con la distancia, los mayores terremotos han causado ondas de Love que pueden rodear al planeta muchas veces antes de desaparecer. Este tipo de ondas no se amortiguan con facilidad, es por eso que pueden llegar a ser muy destructivos en el epicentro.
Las ondas de Love se llaman así en honor a Augustus Edward Hough Love, quien las predijo matemáticamente en 1991.[4]
Sismógrafos y magnitud de los sismos
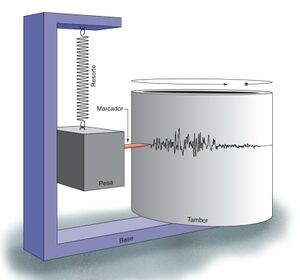
El instrumento que se usa para medir los movimientos de la tierra se le denomina sismógrafo. Este instrumento consiste en un sensor llamado sismómetro que detecta el movimiento del suelo. Este último componente está conectado a un sistema de registro.
La idea básica de un sismógrafo sencillo que mide los movimientos verticales del suelo puede ser vista como un peso suspendido y conectado a un resorte que este a su vez está conectado a una base que se mueve con los movimientos de la tierra. El movimiento relativo entre el peso y la base proporciona una medida del movimiento vertical de la tierra. El sistema de registro consiste en un tambor que gira en la base y un marcador acoplado a la masa. El movimiento relativo entre el peso y la base se registra en el tambor a través de unos registros sísmicos, los cuales se conocen como sismogramas.
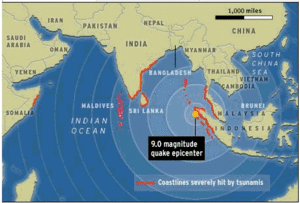
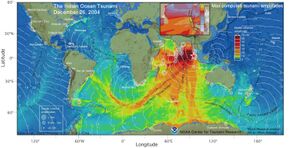
Actualmente, los sismógrafos son electrónicos; en vez de pesas y bases usan voltajes eléctricos registrados en una computadora. Los que son usados en estudios de terremotos son sumamente sensibles a los movimientos de la tierra (pueden llegar a detectar movimientos de 1/10.000.000 de centésima en lugares quietos). Los terremotos más fuertes, como el de las islas Sumatra - Andaman de magnitud 9.1 que ocurrió en el 2004, causan movimientos terrestres alrededor del planeta que pueden llegar a tener varios centímetos de crecimiento.
Con la ayuda de los sismógrafos y sismogramas se han desarrollado modelos matemáticos para establecer escalas de medición de la energía liberada por los terremotos.[8]
Escala sismológica de Richter
Es una escala (de tipo logarítmica) usada para cuantificar en un número la energía liberada por los sismos. Fue nombrada así en honor al sismólogo Charles Francis Richter, quien la desarrolló en colaboración con Beno Gutenberg en 1935. También recibe el nombre de escala $M_{L}$.
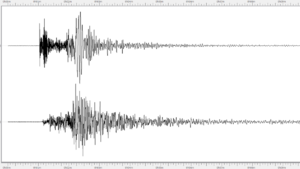
Los números de esta escala se obtienen analizando los datos obtenidos en el sismógrafo. En un terremoto primero llegan las ondas P y después de un tiempo ${\delta}t$ aparecen las ondas S. La diferencia de tiempo ${\Delta}t$ entre la llegada de las ondas, y la amplitud máxima $A$ de las ondas S son los números que se utilizan para calcular el número representativo, el cual es constante para los sismos que liberan la misma cantidad de energía. La fórmula es:
$M = \log_{10} A + 3 \log_{10} (8 \Delta t) - 2.92 = \log_{10} \left({A\cdot\Delta t^3 \over 1.62}\right) \,\!$
Donde $M$ representa la magnitud del terremoto; $A$ es la amplitud máxima de las ondas, y ${\Delta}t$ es el tiempo transcurrido desde el inicio de las ondas P hasta el de las ondas S. Las valores constantes de las fórmulas fueron calculados por Ritcher cuando estudiaba los sismogramas que se obtenían de los sismos que ocurrían en el sur de California.
El logaritmo utilizado en la fórmula hace que los valores de $M$ determinado por los datos agregados en la fórmula aumenten o disminuyan de forma logarítmica y no de forma lineal. La naturaleza de la fórmula matemática muestra teóricamente que las magnitudes no tienen mínimo o máximo, lo cual implica que se pueden llegar a medir magnitudes negativas de sismos. Los sismógrafos más sensibles pueden llegar a detectar magnitudes negativas.
Para introducir el logaritmo Ritcher se baso en la escala estelar para medir el brillo de las estrella.
En la sismología mundial se utiliza esta escala para terremotos de magnitud entre 2,0 hasta 6,9 y de profundidad no mayor a 400 km. Para magnitudes mayores a 6.9 se suele utilizar la escala sismológica de magnitud de momento ya que es más precisa para energías mucho mayores. En ocasiones, los medios mal interpretan los datos diciendo cosas como "terremoto de magnitud 8.0 en la escala de Ritcher en...", cuando en realidad, a partir de números mayores a 6.9 las magnitudes se registran utilizando la escala sismológica de magnitud de momento.[9]
Escala sismológica de magnitud de momento
También se le llama escala $M_{W}$ y es la escala sucesora de la de Ritcher. Es superior a esta debido a que es más precisa cuando se miden cantidades muy grandes en terremotos que liberan una gran cantidad de energía. Fue desarrollada por Thomas C. Hanks y Hiroo Kanamori en 1979.
La ventaja de esta escala es que no se satura con valores de energía muy grandes, además de eso, también coinciden sus valores con los de otras escalas (por ejemplo, sus magnitudes coinciden y continúan con los de la escala de Richter). Las centros sismológicos como National Earthquake Information Center usan esta escala para terremotos muy fuertes.
Como en los otros modelos, la magnitud es un número que representa de forma resumida la energía liberada por un sismo. Su fórmula está dada por:
\[ M_{W}={2 \over 3}({\log_{10}({M_{0} \over N*m})-9.1)} \]
En donde $M_{0}$ es la cantidad de energía liberada por el terremoto, la cual esta en unidades de $N*m$, es decir, la fórmula anterior es una conversión de $M_{0}$ a un número escalar para que se pueda entender mejor la magnitud de la energía liberada en escalas sísmicas. $M_{0}$ está dado por:
\[ M_{0} = {\mu}{A}{u} \]
Donde $\mu$ es el módulo de deformación de las rocas que son afectadas por el sismo; $A$ es el área de ruptura a lo largo de la falla donde se originó el sismo; y $u$ es el desplazamiento promedio del área $A$.[10]
Magnitud de los sismos
Los sismos más fuertes ocurren con mucha menor frecuencia, en cambio, el planeta sufre de miles de temblores que no llegan a ser perceptibles. La magnitud más alta registrada fue del terremoto de 9,5 que ocurrió en la Ciudad de Valdivia, Chile, en el año 1960. No se han registrado magnitudes mayores.[10]
| Magnitud (ML para magnitud 2.0-6.9 y MW para magnitudes Mayores a 6,9) | Denominación del sismo | Efectos en la superficie | Frecuencia |
|---|---|---|---|
| Menores a 2,0 | Micro | No llegan a ser perceptibles. | Aproximadamente 8000 por día |
| 2,0-2,9 | Menor | Generalmente no son perceptibles. | Aproximadamente 1000 por día |
| 3,0-3,9 | Frecuentemente perceptibles, pero no llegan a producir daños. | 49 000 por año. | |
| 4,0-4,9 | Ligero | Llegan a mover objetos en las habitaciones de las construcciones. Significativo pero con pocas probabilidades de provocar daños. | 6200 por año. |
| 5,0-5,9 | Moderado | Puede causar daños considerables en construcciones débiles o mal construidas. En construcciones bien diseñadas los daños menores o casi nulos. | 800 por año. |
| 6,0-6,9 | Fuerte | Pueden llegar a destruir áreas pobladas, en hasta unos 160 kilómetros a la redonda. | 120 por año. |
| 7,0-7,9 | Mayor | Puede causar serios daños en extensas zonas. | 18 por año. |
| 8,0-8,9 | Épico o Cataclismo | Puede causar graves daños en zonas de varios cientos de kilómetros. | 1-3 por año. |
| 9,0-9,9 | Devastadores en zonas de varios miles de kilómetros. |
1-2 en 20 años. |
Dinámica de suelos y parámetros relevantes
Los módulos más simples y usados en la caracterización de la respuesta sísmica de masas de suelo, utilizan como parámetro fundamental el módulo de corte G y la razón de amortiguamiento D[5].
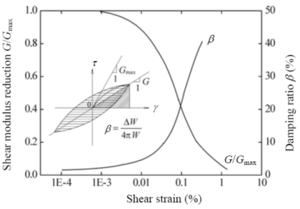
El módulo de corte G de un suelo corresponde a la resistencia de éste ante el desarrollo de deformaciones por corte. La razón de amortiguamiento D está asociada a las características disipativas que presenta el suelo por solicitaciones ( la resultante de las fuerzas externas en los elementos en el terreno), estás generalmente son cíclicas. Dado que los problemas generalmente asociados a vibraciones sísmicas son pequeñas deformaciones, un modelo lineal para describirlos funciona bastante bien. Sin embargo, si las deformaciones son mayores, pueden ajustarse de manera aproximada modelos lineales equivalentes que permitan describir su comportamiento con base en la determinación de leyes de degradación. Vucetic estableció diferentes intervalos de deformación para perturbaciones por corte cíclico donde los límites están definidos por la degradación de la rigidez. Así, es posible definir rangos de deformaciones muy pequeñas, deformaciones medias y grandes deformaciones. La variación de las propiedades del material en función de las deformaciones se observa en las denominadas curvas de degradación de rigidez y razón de amortiguamiento[5] Fig 1.
Existen otros factores que definen el valor de los umbrales de deformación también conocido como límite elástico el cual es el punto en el que un material no puede seguir deformándose y cuando se excede este límite por la aplicación de un esfuerzo, se produce una deformación permanente,un factor es la tensión media de confinamiento, en donde las deformaciones umbrales aumentan de valor para las tensiones de confinamiento mayores.
Degradación de rigidez y disipación de energía
El suelo no responde linealmente y por tanto la rigidez es función del nivel de deformaciones. Además la capacidad de disipar energía aumenta a medida que aumenta el nivel de deformaciones. Tanto la degradación como disipación de energía dependen, al igual que las deformaciones umbrales, de la tensión media de confinamiento y plasticidad del suelo. Algunos otros factores que afectan la degradación de la rigidez y la disipación de energía son la densidad, la historia tensional del depósito de suelos, la velocidad de carga y la duración (número de ciclos). Se ha mostrado que:
- Un aumento en el índice de vacíos disminuye la rigidez, y aumenta la disipación de energía.
- La rigidez no es afectada por la tasa de deformación en suelos de baja plasticidad, en el rango de muy pequeñas deformaciones.
Respecto de la disipación de energía, se ha determinado que la frecuencia de la solicitación aplicada controla éste fenómeno, definiéndose bandas de frecuencias para las cuales la disipación de energía es constante, y otras bandas donde es variable.Para frecuencias en el amplio rango de 0.001-100 Hz, se ha determinado que la disipación de energía es independiente de la frecuencia. Finalmente, otro parámetro que controla el comportamiento dinámico de un suelo está definido por la duración de la solicitación cíclica.
Amplificación dinámica
Este efecto considera la diferencia entre la frecuencia de las ondas sísmicas y la frecuencia natural del depósito sedimentario. Una estimación de la frecuencia natural del un depósito de suelos es: $ T=\frac{4H}{V_s}$ Donde $V_s$ es la velocidad de onda de corte (en [m/s]), H es la potencia del sedimento en metros y T es el período de natural del depósito sedimentario, en Hz. Por ejemplo, un depósito con una velocidad de 340 m/s y un espesor de 30 m, tiene una frecuencia natural de 2.83 Hz, mientras que para un depósito con 100 m de espesor la frecuencia natural es de 0.85 Hz.
Si la frecuencia de la onda sísmica es aproximadamente igual al período natural del depósito se produce amplificación incrementándose la amplitud del movimiento del suelo significativamente. Así pues, los fenómenos que contribuyen a la amplificación de la señal sísmica están relacionados directamente con la velocidad de las ondas sísmicas de corte en el depósito.
Bibliografía
- https://es.wikipedia.org/wiki/Elasticidad_(mec%C3%A1nica_de_s%C3%B3lidos)
- http://www.eis.uva.es/reic/Elas_Web/teoria/ELAS5.pdf
Aportación de: Amisaday (discusión)
Gustavo.uami12 (discusión) 18:27 8 jul 2020 (CDT)
- ↑ Nacional, I. (2020). Sismología en el IGN. Retrieved 4 July 2020, from https://www.ign.es/web/ign/portal/sis-teoria-general
- ↑ 2,0 2,1 2,2 2,3 J.M. Espinola; Z. Jiménez (1994). Terremotos y ondas sísmicas. Una breve introducción.
- ↑ Compresibilidad (2020). Recuperado de https://es.wikipedia.org/wiki/Compresibilidad#:~:text=La%20compresibilidad%20es%20una%20propiedad,determinada%2C%20manteniendo%20constantes%20otros%20par%C3%A1metros.
- ↑ 4,0 4,1 4,2 R. Madariaga (1989). Propagación de ondas sísmicas en el campo cercano.
- ↑ 5,0 5,1 5,2 5,3 Ochoa Cornejo, F. (2007). Caracterización geotécnica a través del uso de ondas Rayleigh (Maestría). Universidad de Chile.
- ↑ Olmo, M., & Nave, R. (2020). Seismic Waves. Retrieved 4 July 2020, from http://hyperphysics.phy-astr.gsu.edu/hbasees/Waves/seismic.html
- ↑ Pant, S. (2014). Lamb Wave Propagation and Material Characterization of Metallic and Composite Aerospace Structures for Improved Structural Health Monitoring (SHM) (Postdoctoral). Carleton University Ottawa, Ontario.
- ↑ Incorporated Research Institutions for Seismology (2020). ¿Cómo trabaja un sismógrafo?
- ↑ Hanks, Thomas C.; Kanamori, Hiroo (1979). A moment magnitude scale.
- ↑ 10,0 10,1 Utsu, Tokuji (2002). Relationships between Magnitude Scales.