Ondas: pinzas opticas y Biofisica
Estas son algunas fórmulas de prueba
Sobre pinzas ópticas y sus aplicaciones en Biofísica
En construcción por Eduardo González Ramírez, Materia: Fenómenos ondulatorios
Algunos conceptos preliminares
La Teoría Electromagnética de la luz y los fotones como una descripción cuántica
El trabajo de James Clerk Maxwell ylos desarrollos posteriores desde finales del siglo XIX pusieron de manifiseto que la luz tiene naturaleza electromagnética. La electrodinámica clásica conduce a la idea de una transferencia contínua de energía por medio de ondas electromagnéticas. En cambio, el punto de vista más moderno de la electrodinámica cuántica describe las interacciones elctromagnéticas y el transporte de energía en términos de "partículas" elementales sin masa, denominadas fotones. La naturaleza cuántica de la energía radiante no es siempre evidente, ni tampoco de interés práctico en óptica. Hay situaciones en las cuales el equipo de detección es tal que es imposible distinguir cuantos individuales. Si la longitud de onda de la luz es pequeña en comparación con el aparato, podrían utilizarse, como primera aproximación, las técnicas de óptica geométrica. Un tratamiento algo más preciso, que es aplicable también cuando las dimensiones del aparato son pequeñas, es el de la óptica física en la que la propiedad dominante de la luz es su naturaleza ondulatoria. Por lo que al estudio clásico de la óptica físsica se refiere, será más que suficiente tratar la luz como una onda electromagnética.
El tratamiento mecánico-cuántico asocia una ecuación de onda con una partícula, sea ésta un fotón, electrón, protón, etc. En el caso de partículas materiales, los aspectos ondulatorios se introducen por medio de la ecuación de campo, conocida como ecuación de Schrodinger. Para la luz, tenemos una representación de la naturaleza ondulatoria en la forma de las ecuaciones de campo electromagnético de Maxwell. Con éstas como punto de partida se puede construir una teoría mecánico-cuántica de fotones y su interaccioón con las cargas. La doble naturaleza de la luz se pone de manifiesto por el hecho de que se propaga en el espacio como lo hace una onda, demostrando, sin embargo, un comportamiento de partícula durante los procesos de emisión y absorción cuando existe interacción con la materia. La energía radiante electromagnética en estos casos es emitida y absorbida en cuantos o tambieén llamados fotones y no de forma contínua como sucede con una onda clásica. No obstante, su movimiento a través de una lente, un agujero o conjunto de rendijas, está supeditado a sus características ondulatorias (tal es el caso de los efectos de interferecia y difracción).
El fotón tiene masa cero y, por consiguiente, puede imaginarse que en un haz de luz hay un número sumamente grande de fotones de "baja energía", por que dentro de ese modelo, haces muy densos de fotones actúan en promedio para producir campos clásicos bien definidos. La energía transportada por un gran número de fotones es, en promedio, equivalente a la energía transferida por una onda electromagnética clásica. Por tales razones en algunas condiciones podemos considerar que la luz es una onda electromagnética clásica, teniendo en cuenta el hecho de que hay situaciones para las cuales esta descripción es inadecuada (como por ejemplo cuando se considera la descripción teórica del efecto fotoeléctrico.
Las ecuaciones de Maxwell
En electromagnetismo, las ecuaciones de Maxwell son un conjunto de cuatro ecuaciones que fueron primeramente presentadas como un grupo notable en 1884 por Oliver Heaviside en conjunto con Willard Gibbs. Estas ecuaciones habían aparecido en una publicación de Maxwell en 1861 titulada On Physical Lines of Force.
Estas describen la interrelación entre los campos eléctricos, los campos magnéticos, la carga eléctrica y la corriente eléctrica, y Maxwell fué el creador de solo una de estas ecuaciones por sí mismo (vía la modificación de una ecuación que ya existía), el las derivó todas independientemente en conjunción con su modelo de vórtice molecular de las líneas de fuerza de Faraday.
Maxwell introdujo un término extra a la ley circuital de Ampère la cual es una derivada temporal del campo eléctrico y conocida como la corriente de desplazamiento de Maxwell. Esta modificación es el aspecto más significativo del trabajo de Máxwell en electromagnetismo.
En el artículo de Maxwell de 1865 titulado A Dynamical Theory of the Electromagnetic Field Versión modificada de Maxwell de la ley circuital de Ampère le permitió derivar la ecuación de onda electromagnética, demostrando teóricamente que la luz es una onda electromagnética con velocidad de propagación c. Esta formulación contenía 20 ecuaciones de 20 variables. En 1873 Maxwell intentó una formulación simplificada que finalmente no resultó popular. Posteriormente la formulación vectorial resultó especialmente atractiva porque remarcaba las simetrías intrínsecas en las ecuaciones haciendo más fácil su utilización e inspirando aplicaciones posteriores.
Resumen de las "ecuaciones de Maxwell" en notación moderna tanto en su forma Diferencial como Integral
| Nombre | Forma diferencial | Forma integral |
|---|---|---|
| Ley de Gauss: | ||
| Ley de Gauss para el campo magnético (ausencia de monopolos magnéticos): |
||
| Ley de Faraday: | ||
| Ley de Ampère generalizada: |
En la siguiente tabla se proporciona el significado de cada símbolo y su unidad de medida en el SI:
| Símbolo | Significado | Unidad de medida SI |
|---|---|---|
| campo eléctrico | voltio por metro | |
| campo magnético | amperio por metro | |
| desplazamiento eléctrico | culombio por metro cuadrado | |
| desplazamiento magnético | tesla, o weber por metro cuadrado | |
| densidad de carga eléctrica | culombio por metro cúbico | |
| densidad de corriente | amperio por metro cuadrado | |
| vector del elemento diferencial de superficie normal a la superficie S | metros cuadrados | |
| elemento diferencial de volumen encerrado por la superficie S | metros cúbicos | |
| vector del elemento de longitud del contorno que limita la superficie S | metros | |
| divergencia | por metro | |
| rotacional | por metro |
La segunda ecuación es equivalente a afirmar que el monopolo magnético no existe. La fuerza ejercida sobre una partícula cargada por los campos eléctricos y magnético viene dada por la ecuación de la Fuerza de Lorentz:
donde es la carga de la partícula y es la velocidad de ésta.
Las ecuaciones de Maxwell en el vacío, sin cargas ni corrientes
El vacío es un medio lineal, homogéneo, isótropo y no dispersivo. Las constantes de proporcionalidad en el vacío son ε0 y μ0.
Como no hay ni corriente ni carga eléctrica en el vacío, las ecuaciones de Maxwell en espacio libre son:
Estas ecuaciones tienen soluciones sencillas para ondas planas sinusoidales, con campos eléctricos y magnéticos con direcciones ortogonales entre ellos y ortogonales a la dirección de propagación. Su velocidad de propagación es
Maxwell descubrió que esta cantidad c era simplemente la velocidad de la luz en el vacío, por lo que la luz es una forma de radiación electromagnética. Los valores aceptados actualmente para la velocidad de la luz y para la permitividad y permeabilidad se resumen en la siguiente tabla:
| Símbolo | Nombre | Valor numérico | Unidad de medida SI | Tipo |
|---|---|---|---|---|
| Velocidad de la luz | definido | |||
| Permitividad Eléctrica | derivado | |||
| Permeabilidad Magnética | definido |
Momento y presión de Radiación

En 1619, Johannes Kepler sugirió que era la presión de la luz solar lo que desviaba la cola de un cometa de manera que siempre apuntaba lejos del Sol. Esta argumentación cautivó especialmente a los defensores futuros de la teoróa crpuscular de la luz. Dspués de todo, ellos imaginaban un haz de luz como un flujo de parículas y dicho flujo ejercería, naturalmente, una fuerza al bombardear la materia. Durante algún tiempo parecía como si este efecto permitiera establecer, al final, la superioridad de la teoría corpuscular sobre la ondulatoria, pero todos los experimentos que se realizaron en esa direccción no consiguieron detectar la fuerza de la radiación, así que el interés se fué apagando poco a poco. Irónicamente, fué Maxwell en 1873 quien volvió a sacar este tema estableciendo, en teoría, que las ondas ejercen efectivamente una presión. "En un medio en el que las ondas se propagan", escribió Maxwell, "hay una presión en la dirección norml a las ondas, numéricamente igual a la energía en una unidad de volumen". Cuando una onda electromagnética incide en la superficie de un material, interacciona con las cargas que constituyen el material masivo. Independientemente de que la onda sea absorbida parcialmente o reflejada, ejerce una fuerza sobre aquellas cargas y, por consiguiente, sobre la superficie misma. Por ejemplo, en el caso de un buen conductor, el campo eléctrico de la onda genera una corrientes mientras que su campo magnético genera unas fuerzas sobre esas corrientes.
Es posible calcular la fuerza resultante por la teoría electromagnética, en la que la segunda Ley de Newton (según la cuál la fuerza equivale al ritmo de cambio del momento) sugiere que la onda misma lleva un momento. Realmente, cuando tenemos un flujo de energía, es normal pensar qeu haya un momento asociado - se trata de los dos aspectos relacionados de tiempo y espacio del movimiento -.
Como demostró Maxwell, la presión de radiación, \mathcal{P} , equivale a la densidad de energía de la onda electromagnética.
Para un vacío sabemos que
Pinzas Ópticas
Una pinza óptica es un instrumento científico que usa un rayo láser para proveer una fuerza atractiva o repulsiva, dependiendo del emparejamiento de índice (típicamente en el orden de pico Newtons) para sostener y mover físicamente objetos dieléctricos microscópicos. Las pinzas ópticas han sido particularmente exitosas en el estudio de una variedad de sistemas biológicos en los años recientes.
Historia y desarrollo
La detección de la dispersión óptica y las fuerzas de gradiente sobre partículas micrométricas fué reportado por primera vez en 1970 por Arthur Ashkin[1], trabajando en los Laboratorios Bell. Años después, Ashkin y sus colegas reportaron la primera observación [2] de lo que es ahora referido comúnmente como una trampa óptica: un haz de luz altamente enfocado capaz de sostener partículas microscópicas estables en tres dimensiones.
Uno de los autores de este artículo pionero de 1986, Steven Chu, podría haber llegado a ser utilizado con pinzas ópticas en su trabajo sobre enfriamiento y atrapamiento de átomos. Esta investigación le valió a Chu el Premio Nobel en Física de 1997.[3]. En una entrevista[4], Steven Chu describió como Askhin había visualizado por primera vez el uso de las pinzas ópticas como un métodopara atrapar átomos. Ashkin fué capaz de atrapar partículas mas grandes ( de 10 a 10,000 nanometros de diámetro) pero Chu extendió estas técnicas para el atrapamiento de átomos (0.1 nanómetros de diámetro).
A finales de 1980,Arthur Ashkin y sus colegas aplicaron primero la tecnología a las ciencias biológicas , usándola para atrapar un virus de mosaico del tabaco individual y la bacteria Escherichia coli [5]. A través de la década de los 90's y después, investigadores como Carlos Bustamante, James Spudich, y Steven Block fueron los pioneros en el uso de la trampa óptica espectroscopía de fuerza para caracterizar los motores biológicos a escala molecular. Estos motores moleculares son ubicuos en biología, y son los responsables de la locomoción y la acción mecánica dentro de la célula. Las trampas ópticas permitieron a estos biofísicos observar las fuerzas y la dinámica de los motores a un nivel de nano-escala o de molécula-única; la trampa óptica de espectroscopía de fuerza ha permitido desde entonces llegar a un mayor entendimiento de la naturaleza estocástica de estas fuerzas generadoras en la moléculas.
Las pinzas ópticas han probado ser útiles también en otras áreas de la Biología. Por ejemplo, en 2003 las técnicas de las pinzas ópticas fueron aplicadas en el campo de la clasificación celular (cell sorting); creando una gran intensidad óptica sobre el área de llenada con muestra micro-biológica, la célula puede ser clasificada por sus características ópticas intrínsecas.[6] [7]. En el 2004 las pinzas ópticas hicieron el salto desde las grandes, complicadas y costosas máquinas a mucho más simples, pequeñas, poco costosas y recientemente sistemas portables con la introducción de los DLBT (Diode Laser Bar Trapping) ;sitemas liderados por Applegate et al. en la Colorado School of Mines[8]. Las pinzas ópticas también han sido usadas para probar el citoesqueleto, medir las propiedades visco-elásticas de biopolímeros, y estudiar la motilidad celular.
La física de las pinzas ópticas
Descripción General
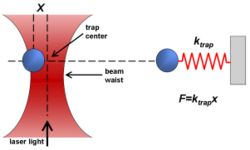
Las pinzas ópticas son capaces de manipular partículas dieléctricas tanto de tamaño nanométrico como micrométrico ejerciendo fuerzas extremadamente pequeñas por medio de un haz láser altamente enfocado. El haz es típicamente enfocado enviándolo a través de un objetivo microscópico. El punto más angosto del haz enfocado, conocido como la cintura del haz, contiene un gradiente de campo eléctrico muy fuerte. Resulta ser que las partículas dieléctricas son atraídas a lo largo del gradiente a la región del campo eléctrico más fuerte, el cuál es el centro del haz. La luz láser también tiende a jercer una fuerza sobre las partículas en el haz a lo largo de la dirección de propagación del haz. Esto es fácil de comprender si imaginamos a laluz como un grupo de pequeñas partículas, cada un a de ellas ejerciendo sobre la pequeña partícula dieléctrica en su camino. Esto es conocido como la fuerza de dispersión y cuyo resultado es el de la partícula siendo desplazada ligeramente abajo de la de la posición exacta de la cintura del haz, como se puede ver en la figura.
Las pinzas ópticas son instrumentos muy sensibles y son capaces de manipular y detectar desplazamientos sub-nanométricos para partículas dieléctricas sub-micrónicas.[9] Por esta razón son comúnmente utilizadas para manipular y estudiar moléculas individuales por la interacción con una cuenta que ha sido adjuntada a esa molécula. El ADN ,las proteínas y las enzimas que interactúan con esta son comúnmente estudiadas de esta forma.
Para mediciones científicas cuantitativas, la mayoría de las trampas ópticas son operadas de tal forma que la partícula dieléctrica raramente se mueve lejos del centro de la trampa. La razón de esto es que la fuerza aplicada a la partícula es lineal con respecto a su desplazamiento desde el centro de la trampa mientras el desplazamiento sea pequeño. De esta forma, una trampa óptica puede ser comparada con un resorte simple, que sigue la ley de Hooke.
Visión detallada de las pinzas ópticas
Una explicación apropiada del comportamiento del atrapamiento óptico depende del tamaño de la partícula atrapada relativo a la lonkgitud de onda de la luz utilizada para atraparla. En casos en donde las dimensiones de la partícula son mayores que esta longitud de onda, un simple tratamiento de rayos es suficiente. Por otro lado, si la longitud de onda de la luz excede a las dimensiones de la partícula, entonces las partículas deberán ser tratadas como pequeños dipolos elécticos en un campo eléctrico.
El enfoque de óptica de rayos
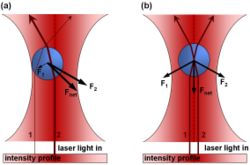
En casos en donde el diámetro de la partícula atrapada es significativamente mayor que la longitud de onda de la luz, el fenómeno de atrapamiento pude ser explicado usando un aóptica de rayos o geométrica. Como se muestra en la figura, lo rayos individuales de luz emitida desde el láser serán refractados en la medida en que entran y salen de la cuenta dieléctrica. Como un resultado, el rayo saldrá en una dirección distinta a la que inicialmente ingresó. Dado que la luz tiene un momento asociado a ella, este cambio en dirección de la luz indica que su momento ha cambiado. Debido a la Tercera Ley de Newton, tendrá que haber un cambio de momento igual y opuesto sobre la partícula.
La mayoría de las trampas ópticas tienen un perfil de intensidad de haz Gaussiano (modo TEM00) . En este caso, si la partícula es desplaxada desde el centro del haz, como en la figura (a), la partícula tiene una fuerxa neta que la regresa al centro de la trampa debido a que haces más intensos impelen un cambio de momento mayor hacia el centro de la trampa que los haces menos intensos, lo cuales impelen un cambio de momento menor lejos del centro de la trarmpa. El cambio de momento neto o fuerza, regresa a la partícula al centro de la trampa.
Si la partícula está localizada en el centro del haz, entonces los rayos de luz individuales son refractados a través de la partícula simétricamente, resultando esto en una fuerza lateral nula. La fuerza neta en este caso está a lo largo de la dirección axial de la trampa, la cual cancela la fuerza de esparcimiento de la luz láser. La anulación de esta fuerza gradiente axial con la fuerza de esparcimiento es lo que causa que la cuenta se mantenga estable ligeramente alejada de la cintura del haz.
La aproximación del dipolo eléctrico
En casos en los que el diámetro Ide la partícula atrapada es significativamente mas pequeña que la longitud d onda de la luz, las condiciones del esparcimiento de Rayleigh son satisfechas y la partícula puede ser tratada como un punto dipolo en un campo electrmagnético inhomogéneo. La fuerza aplicada sobre un dipolo en un campo electromagnético se conoce como la fuerza de Lorentz,
La fuerza sobre el dipolo puede ser calcula sustituyendo dos términos del campo eléctrico en la ecuación anterior, uno para cada carga. La polarización de un dipolo es donde es la distancia entre las dos cargas. Para un dipolo puntual, la distancia es infinitesimal, Tomando en cuenta que las dos cargas tienen signos opuestos, la fuerza toma la forma
Notemos que se cancela. Multiplicando todo por la carga, , convertimos posición, , en polarización, ,
En donde en la segunda igualdad se ha asumido que la partícula dieléctrica es lineal (i.e. ).
En los pasos finales, dos igualdades serán utilizadas: (1) Una igualdad de análisis vectorial, (2) Una de las ecuaciones de Maxwell.
Primero, la igualdad vectorial será insertada para el primer término en la fuerza de la ecuación de arriba. La ecuación de Maxwell será sustituida en el segundo término de la igualdad vectorial. Después los dos términos que contienen derivadas en el tiempo pueden ser combinadas en un solo término.[10]
El segundo término en la última igualdad es la derivada temporal de una cantidada que se relaciona a través de una constante multiplicativa que es el vector de Poynting, que describe la potencia por unidad de área que pasa a través de una superficie. Asumiendo que la potencia del láser es constante,la derivada de este término es ceroy la fuerza se puede escribir como
El cuadrado de la magnitud del campo eléctrico es igual a la intensidad del haz como una función de la posición. De esta forma, el resultado indica que la fuerza sobre la partícula dieléctrica, cuando es tratada como un dipolo puntual, es proporcional al gradiente a lo largo de la intensidad del haz. En otras palabras, la fuerza gradiente descrita aquí tiende a atraer a la partícula a la región de más alta intensidad. En realidad, la fuerza de dispersión de la luz actúa en contra de la fuerza de gradiente en la dirección axial de la trampa, resultando esto en una posición de equilibrio que es deplazada ligeramente por abaja de el máximo de intensidad. La fuerza de esparcimiento depende linealmente de la intensidad del haz, la sección eficaz del haz y el índice de refracción de el medio en donde se encuentra la trampa (i.e. agua).
Diseño experimental, construcción y operación
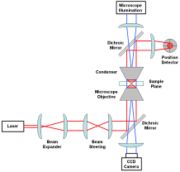
La configuración más básica de pinza óptica incluirá mas omenos los siguientes componentes: un láser (usualmente Nd:YAG), un expansor del haz, algunos elementos ópticos para dirigir la localización del hazen el mismo plano, un objetivo de microscopio y un condensador para crear la trampa en el mismo plano, un detector de posición (i.e. un fotodiodo de cuadrante) para medir los desplazamientos del haz y una fuente de iluminación microscópica acoplada a una cámara CCD.
El láser de Nd:YAG (longitud de onda de 1064 nm) es la elección de láser más común debido a que los especímenes biológicos son en su mayoría transparentes a logitudes de onda láser alrededor de 1000 nm. Esto asegura un bajo coeficiente de absorción , minimizando el daño al especímen, algunas veces referido como opticution en inglés. Quizá la consideración más importante en una pinza óptica es la elección del objetivo. Una trampa estable requiere que la fuerza de gradiente, que depende de la apertura numérica (AN) del objetivo sea más grande que la fuerza de dispersión. Objetivos adecuados típicamente tienen una AN entre 1.2 y 1.4.[11]
Existen alternativas disponibles, pero quizá el método más simple para detección de la posición tiene que ver con la visualización de la trampa láser exitando a la cámara en donde se encuentra la muestra dentro de un fotodiodo de cuadrante. Las deflecciones laterales del haz son medidas de forma similar a como se hace cuando se utiliza el microscopio de fuerza atómica (MFA).
Expandiendo el haz emitido desde el láser para llenar la la apertura del objetivo resultará en un punto difractado-limitado más apretado.[12] Mientras que la traslación lateral de la trampa relativa a la muestra puede ser lograda por el portaobjetos del microscopio, la mayoría de las configuraciones de pinzas ópticas implementan óptica adicional diseñada para trasladar el haz para dar un grado extra de libertad traslacional. Esto se puede hacer trasladando el primero de los dos lentes llamado "Direccionador del haz" en la figura(Beam Steering). Por ejemplo, la traslación de ese lente en el plano lateral resultará en un haz deflectado lateralmente desde lo que es mostrado en la fugura. Si la distancia entre los lentes de direccionamiento del haz y el objetivo es escogida adecuadamente, esto corresponderá a una deflexión antes de que el objetivo entre y resultando en una traslación lateral en el mismo plano. La posición de la cintura del haz, que está en el foco de la trampa óptica, puede ser ajustada por un desplazamiento axial del lente inicial. Tal desplazamiento axial causa que el haz diverja o converja ligeramente, resultado de lo cual es una posición axial desplazada de la cintura del hazen la cámara de la muestra. Una explicación muy clara ha sido presentada por Joshua W. Shaevitz un estudiante graduado en el Block Lab en Stanford University.[13]
La visualización del plano de la muestra se logra usualmente a través de iluminación vía una fuente de luz separada acoplada dentro del camino óptico en la dirección opuesta usando un espejos dicróicos. Esta luz incide sobre una camara CCD y puede ser vista en un monitor externo o usada para trazar a la partícula atrapada vía la posición por seguimiento de video.
- ↑ Ashkin, A. "Phys. Rev. Lett. 24, 156-159", (1970)
- ↑ A Ashkin, J M Dziedzic, J E Bjorkholm and S Chu, Opt. Lett. 11, 288-290, 1986.
- ↑ Hill, Murray (November 1987). "wrote the book on atom trapping". Retrieved June 25, 2005.
Interview conducted for internal newsletter at Bell Labs. Contains confirmation of Ashkin as the inventor of optical trapping and provides information on the 1997 Nobel Prize in Physics. - ↑ "Conversations with History: An Interview with Steven Chu" (2004), Institute of International Studies, UC Berkeley. Last accessed on September 2, 2006.
- ↑ Ashkin, A. et al "Science vol. 235, iss. 4795, pp. 1517" (1987)
- ↑ Macdonald MP, Spalding GC, Dholakia K, "Microfluidic sorting in an optical lattice., Nature (2003); 421: 421-424.
- ↑ Koss BA, Grier DG, "Optical Peristalsis"
- ↑ Applegate, Jr. R. W. et al Optics Express vol. 12, iss. 19, pp. 4390 (2004)
- ↑ Moffitt JR, Chemla YR, Izhaky D, Bustamante C, "Differential detection of dual traps improves the spatial resolution of optical tweezers", PNAS (2006); 103(24): 9006-9011.
- ↑ Gordon JP, "Radiation Forces and Momenta in Dielectric Media", Physical Review A (1973). 8(1): 14-21.
- ↑ Neuman KC, Block SM, "Optical trapping", Review of Scientific Instruments (2004); 75(9): 2787-2809.
- ↑ Svoboda K, Block SM, "Biological Application of Optical Forces", Annual Reviews of Biophysics and Biomolecular Structure (1994); 23:247-285.
- ↑ Shaevitz JW, "A Practical Guide to Optical Trapping" (August 22, 2006). Last accessed on September 12, 2006.

























































![\mathbf{F}=\alpha\left[\left(\mathbf{E}\cdot\nabla\right)\mathbf{E}+\frac{d\mathbf{E}}{dt}\times\mathbf{B}\right],](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e0e6ffbc4d0792b0fc171528ff3d912e17c0bc82)



![\mathbf{F}=\alpha\left[\frac{1}{2}\nabla E^2-\mathbf{E}\times\left(\nabla\times\mathbf{E}\right)+\frac{d\mathbf{E}}{dt}\times\mathbf{B}\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7f3f994d4d5f7b8ed86563e2b4706338f43cbd6d)
![\mathbf{F}=\alpha\left[\frac{1}{2}\nabla E^2-\mathbf{E}\times\left(-\frac{d\mathbf{B}}{dt}\right)+\frac{d\mathbf{E}}{dt}\times\mathbf{B}\right]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3f01276eee0c16da804d2d47bf49b896a7bd8695)
![\mathbf{F}=\alpha\left[\frac{1}{2}\nabla E^2+\frac{d}{dt}\left(\mathbf{E}\times\mathbf{B}\right)\right].](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d4c54d9ad6848d62c8bd9820e0e1b890b84279e2)