Diferencia entre revisiones de «Ondas: ondas longitudinales»
Sin resumen de edición |
|||
| (No se muestran 13 ediciones intermedias de 2 usuarios) | |||
| Línea 8: | Línea 8: | ||
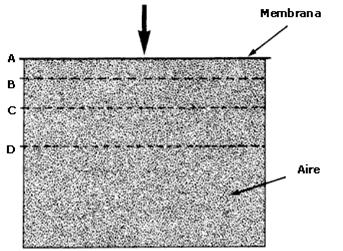
Las variaciones de presión ''(compresión y rarefacción)'' en un sistema originan el sonido | Las variaciones de presión ''(compresión y rarefacción)'' en un sistema originan el sonido | ||
La compresión solo consistía entonces en tratar de juntar las partículas del aire. | |||
: | [[Imagen:compresion1.jpg|center|thumb|400x300px|Figura 1. Al apretar la membrana, el aire en la zona AB se comprime.]]. | ||
La rarefacción es la disminución de la densidad de un cuerpo gaseoso. | |||
[[Imagen:rarefacción.jpg|center|thumb|400x300px|Figura 2. Al estirar la membrana, el aire en la zona AB se vuelve menos denso, es decir, se rarifica.]]. | |||
==''' Acústicas''' == | ==''' Acústicas''' == | ||
| Línea 23: | Línea 25: | ||
En equilibrio el gas permanece uniforme, con una presión constante. | En equilibrio el gas permanece uniforme, con una presión constante. | ||
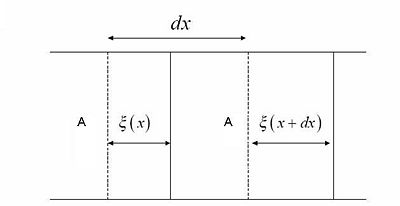
Supongamos que | Supongamos que <math> \mathbf{\xi\,} ( \mathbf{x})</math> es el desplazamiento del aire durante el paso de una onda sonora. Tomamos un elemento de volumen de aire de espesor dx, localizado entre dos planos de área <math> \mathit{A}</math> , perpendiculares a la dirección de propagación, situados en las coordenadas '''<math> \mathbf{x}</math>''' y '''<math> \mathbf{x}+{dx} </math>.'''El volumen antes de que pase la onda sonora es <math> \mathit{A} \mathbf{dx}</math> = <math>\mathbf{V} </math>. | ||
Bajo estas condiciones se realiza un pequeño desplazamiento del gas, limitado por los planos | Bajo estas condiciones se realiza un pequeño desplazamiento del gas, limitado por los planos <math> \mathit{A}</math>. | ||
< | |||
Al pasar la onda sonora, el plano izquierdo se desplaza una distancia | [[Imagen:volumen1.jpg|center|thumb|400x300px|Figura 3. Se muestra el desplazamiento de un gas , en este caso aire , confinado en cierta área.]]. | ||
Al pasar la onda sonora, el plano izquierdo se desplaza una distancia <math> \mathbf{\xi\,} ( \mathbf{x})</math> , y el plano derecho se desplaza una distancia | |||
<center><math> \mathit{\xi\,} ( \mathbf{x}+{dx} ) \approx \mathit{\xi\,} ( \mathbf{x}) + \frac{\partial\xi\,}{\partial\mathbf{x}}{\mathrm{dx}} </math></center> | <center><math> \mathit{\xi\,} ( \mathbf{x}+{dx} ) \approx \mathit{\xi\,} ( \mathbf{x}) + \frac{\partial\xi\,}{\partial\mathbf{x}}{\mathrm{dx}} </math></center> | ||
| Línea 34: | Línea 38: | ||
Por tanto, el incremento de volumen de este elemento será. | Por tanto, el incremento de volumen de este elemento será. | ||
<center><math> \ | <center><math> \mathbf{dV} </math> = <math> \mathit{A} ( \mathbf{\xi\,} ( \mathbf{x} +\mathbf{dx} )- \mathbf{\xi\,}(\mathbf{x}))\approx \mathit{A} \frac{\partial\xi\,}{\partial\mathbf{x}}{\mathrm{dx}} </math></center> | ||
Estudiando el efecto de este incremento de volumen sobre la presión del aire y recordando que el aire, siendo un gas, se encuentra en equilibrio antes de que pase la onda sonora, nos fijamos en la compresibilidad | Estudiando el efecto de este incremento de volumen sobre la presión del aire y recordando que el aire, siendo un gas, se encuentra en equilibrio antes de que pase la onda sonora, nos fijamos en la compresibilidad de este, la cual esta definida por : | ||
<center> <math> \mathbf{K}</math> = <math>-\mathbf{V}\frac{dP}{dV}</math></center> | <center> <math> \mathbf{K}</math> = <math>-\mathbf{V}\frac{dP}{dV}</math></center> | ||
Donde dP es la variación de la presión del aire respecto de su valor en el equilibrio. | Donde <math> \mathbf{dP} </math> es la variación de la presión del aire respecto de su valor en el equilibrio. | ||
En general, K es positiva demostrando que bajo una compresión ( dV < 0) , la presión del aire aumenta, y bajo una dilatación ( dV > 0 ) , la presión del aire | En general, <math> \mathbf{K}</math> es positiva demostrando que bajo una compresión ( <math> \mathbf{dV} </math> < 0) , la presión del aire aumenta, y bajo una dilatación ( <math> \mathbf{dV} </math> > 0 ) , la presión del aire | ||
disminuye. | disminuye. | ||
Así del desplazamiento del aire en cada punto , tenemos que . | Así del desplazamiento del aire en cada punto , tenemos que . | ||
<center><math> \ | <center><math> \mathbf{dP} </math> =<math>-\mathbf{K}\frac{dV}{V}</math>=<math>-\mathbf{K} \frac{\partial\xi\,}{\partial\mathbf{x}}</math></center> | ||
La fuerza generada por el desplazamiento del aire en el elemento seleccionado sobre sus alrededores es igual a la variación de la presión por el área normal <math> \mathit{A} </math>. | |||
Sobre el plano izquierdo, la fuerza es | |||
<center><math> F_{ | <center><math>\mathbf{ F_{izq}}</math> =<math>-\mathit{A}\mathbf{dP}</math>=<math>-\mathbf{K} \frac{\partial\xi\,,( \mathbf{x})}{\partial\mathbf{x}}</math></center> | ||
y sobre el plano derecho | y sobre el plano derecho, | ||
<center><math> F_{ | <center><math> \mathbf {F_{der}}</math> =<math>\mathit{A}\mathbf{dP}</math>=<math>\mathbf{K}\mathit{A} \frac{\partial\xi\,( \mathbf{x} +\mathbf{dx} )}{\partial\mathbf{x}}</math></center> | ||
Aplicando la ecuación de Newton, encontramos la ecuación de movimiento para la masa de aire que se encuentra encerrada en nuestro elemento en cuestión. | Aplicando la ecuación de Newton, encontramos la ecuación de movimiento para la masa de aire que se encuentra encerrada en nuestro elemento en cuestión. | ||
<center><math> \mathbf{m} ( \mathbf{x} )\mathbf{a}(\mathbf{x})</math>= <math> F_{ | <center><math> \mathbf{m} ( \mathbf{x} )\mathbf{a}(\mathbf{x})</math>= <math> \mathbf {F_{izq}+ F_{der}}</math></center> | ||
siendo <math> \mathbf{m} ( \mathbf{x} )</math> la masa de aire del elemento | |||
<center><math> \mathbf{m} ( \mathbf{x} )</math>= <math> \mathbf{\rho}\ | <center><math> \mathbf{m} ( \mathbf{x} )</math>= <math> \mathbf{\rho}\mathit{A}\mathbf{dx}</math></center> | ||
La aceleración del movimiento del aire será la segunda variación temporal de su desplazamiento respecto del equilibrio | La aceleración del movimiento del aire será la segunda variación temporal de su desplazamiento respecto del equilibrio | ||
| Línea 77: | Línea 85: | ||
Hablando en general de la propagación de dos ondas, una onda de desplazamiento y una onda de presión. La velocidad de propagación de las ondas sonoras es | Hablando en general de la propagación de dos ondas, una onda de desplazamiento y una onda de presión. La velocidad de propagación de las ondas sonoras es | ||
<center><math> C_{sonido}</math> = <math> | <center><math> C_{sonido}</math> = <math>\sqrt\frac{K}{\rho}</math></center> | ||
Para determinar la compresibilidad del gas debemos estudiar el comportamiento del aire bajo las compresiones y expansiones sucesivas. En general,la temperatura aumenta en las zonas de compresión y disminuye en las zonas de expansión. Pero la velocidad de la onda sonora es tan grande que no hay tiempo suficiente para que la temperatura se equilibre entre las regiones de expansión y compresión. | Para determinar la compresibilidad del gas debemos estudiar el comportamiento del aire bajo las compresiones y expansiones sucesivas.Si admitimos que las transformaciones que acompañan a la propagación del sonido en el aire (es decir, las compresiones y rarefacciones) tienen carácter adiabático y que el aire se comporta como un '''''gas ideal''''' ,entonces podremos escribir- | ||
<center><math> \mathbf{K}</math>= <math>\mathbf{P}{\gamma}</math></center> | |||
En general,la temperatura aumenta en las zonas de compresión y disminuye en las zonas de expansión. Pero la velocidad de la onda sonora es tan grande que no hay tiempo suficiente para que la temperatura se equilibre entre las regiones de expansión y compresión. | |||
Es decir, la propagación de la onda sonora se realiza de forma adiabática, sin transferencia de energía térmica. En tal caso, de la ecuación de equilibrio de una gas bajo una transformación adiabática tenemos: | Es decir, la propagación de la onda sonora se realiza de forma adiabática, sin transferencia de energía térmica. En tal caso, de la ecuación de equilibrio de una gas bajo una transformación adiabática tenemos: | ||
<center><math> \mathbf{P} \mathbf{V^{\gamma}}</math>= <math> cte</math></center> | <center><math> \mathbf{P} \mathbf{V^{\gamma}}</math>= <math> cte</math></center> | ||
<center><math> \frac{dP}{P} </math> + <math>\mathbf{\gamma}\frac{dV}{V}</math>= 0</center> | |||
donde <math> \mathbf{\gamma}</math>= <math> \frac{C_p}{C_v} </math> , es el cociente de calores especificos, de esta manera obtenemos la compresibilidad del aire. | |||
<center><math> \mathbf{K} </math> =<math>-\mathbf{V}\frac{dP}{dV}</math>= <math>\mathbf{\gamma}\mathbf{P}</math></center> | |||
siendo P la presión en el equilibrio .Por lo tanto , la velocidad del sonido | |||
<center><math> C_{sonido}</math> = <math>\sqrt\frac{\mathbf{\gamma}P}{\rho}</math> = <math>\sqrt\frac{\mathbf{\gamma}P{V}}{m}</math> = <math>\sqrt\frac{\mathbf{\gamma} n{R}{T}}{m}</math> = <math>\sqrt\frac{\mathbf{\gamma}{R}{T}}{M}</math></center> | |||
es proporcional a la raiz cuadrada de la temperatura del gas . Aquí, M es la masa de | |||
un mol de gas. | |||
== Referencias == | |||
[1] Vibrations and Waves in Physics, Autor: Iain G. Main, Editorial: Cambridge, tercera edición | |||
[2] Física para las ciencias de la vida, Autor: Alan H. Cromer, Editorial Reverté | |||
[[categoría:Ondas]] | [[categoría: Ondas]] | ||
Revisión del 11:55 18 dic 2007
Ondas longitudinales
Las ondas sonoras son ondas mecánicas longitudinales, que pueden propagarse en los medios materiales (sólidos, líquidos y gases). Las ondas en las que la perturbación es paralela a la dirección de propagación se denominan longitudinales
1 un ejemplo de estas son la ondas acústicas.
Las variaciones de presión (compresión y rarefacción) en un sistema originan el sonido
La compresión solo consistía entonces en tratar de juntar las partículas del aire.
.
La rarefacción es la disminución de la densidad de un cuerpo gaseoso.
.
Acústicas
Como una simple introducción a las ondas acústicas , consideremos una perturbación longitudinal en un gas confinado en una tuberia cilindrica. En equilibrio el gas permanece uniforme, con una presión constante.
Supongamos que es el desplazamiento del aire durante el paso de una onda sonora. Tomamos un elemento de volumen de aire de espesor dx, localizado entre dos planos de área , perpendiculares a la dirección de propagación, situados en las coordenadas y .El volumen antes de que pase la onda sonora es = .
Bajo estas condiciones se realiza un pequeño desplazamiento del gas, limitado por los planos .
.
Al pasar la onda sonora, el plano izquierdo se desplaza una distancia , y el plano derecho se desplaza una distancia
Por tanto, el incremento de volumen de este elemento será.
Estudiando el efecto de este incremento de volumen sobre la presión del aire y recordando que el aire, siendo un gas, se encuentra en equilibrio antes de que pase la onda sonora, nos fijamos en la compresibilidad de este, la cual esta definida por :
Donde es la variación de la presión del aire respecto de su valor en el equilibrio.
En general, es positiva demostrando que bajo una compresión ( < 0) , la presión del aire aumenta, y bajo una dilatación ( > 0 ) , la presión del aire disminuye.
Así del desplazamiento del aire en cada punto , tenemos que .
La fuerza generada por el desplazamiento del aire en el elemento seleccionado sobre sus alrededores es igual a la variación de la presión por el área normal .
Sobre el plano izquierdo, la fuerza es
y sobre el plano derecho,
Aplicando la ecuación de Newton, encontramos la ecuación de movimiento para la masa de aire que se encuentra encerrada en nuestro elemento en cuestión.
siendo la masa de aire del elemento
La aceleración del movimiento del aire será la segunda variación temporal de su desplazamiento respecto del equilibrio
Con esto, obtenemos
Hablando en general de la propagación de dos ondas, una onda de desplazamiento y una onda de presión. La velocidad de propagación de las ondas sonoras es
Para determinar la compresibilidad del gas debemos estudiar el comportamiento del aire bajo las compresiones y expansiones sucesivas.Si admitimos que las transformaciones que acompañan a la propagación del sonido en el aire (es decir, las compresiones y rarefacciones) tienen carácter adiabático y que el aire se comporta como un gas ideal ,entonces podremos escribir-
En general,la temperatura aumenta en las zonas de compresión y disminuye en las zonas de expansión. Pero la velocidad de la onda sonora es tan grande que no hay tiempo suficiente para que la temperatura se equilibre entre las regiones de expansión y compresión. Es decir, la propagación de la onda sonora se realiza de forma adiabática, sin transferencia de energía térmica. En tal caso, de la ecuación de equilibrio de una gas bajo una transformación adiabática tenemos:
donde = , es el cociente de calores especificos, de esta manera obtenemos la compresibilidad del aire.
siendo P la presión en el equilibrio .Por lo tanto , la velocidad del sonido
es proporcional a la raiz cuadrada de la temperatura del gas . Aquí, M es la masa de un mol de gas.
Referencias
[1] Vibrations and Waves in Physics, Autor: Iain G. Main, Editorial: Cambridge, tercera edición
[2] Física para las ciencias de la vida, Autor: Alan H. Cromer, Editorial Reverté