Diferencia entre revisiones de «Ondas: ondas longitudinales»
| Línea 1: | Línea 1: | ||
== Ondas longitudinales == | == '''Ondas longitudinales''' == | ||
| Línea 9: | Línea 9: | ||
[[Imagen:compresion1.jpg]] | [[Imagen:compresion1.jpg]] | ||
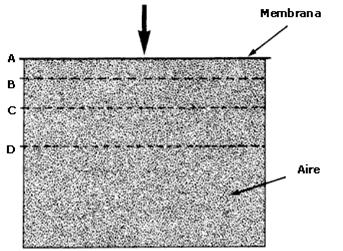
Al apretar la membrana, el aire en la zona AB se comprime. | |||
:*Al apretar la membrana, el aire en la zona AB se comprime. | |||
[[Imagen:rarefacción.jpg]] | [[Imagen:rarefacción.jpg]] | ||
Al estirar la membrana, el aire en la zona AB se vuelve menos denso, es decir, se rarifica. | |||
:*Al estirar la membrana, el aire en la zona AB se vuelve menos denso, es decir, se rarifica. | |||
== Acústicas == | == Acústicas == | ||
Revisión del 00:32 9 dic 2007
Ondas longitudinales
Las ondas en las que la perturbación es paralela a la dirección de propagación se denominan longitudinales
1 un ejemplo de estas son la ondas acústicas.
Las variaciones de presión (compresión y rarefacción) en un sistema originan el sonido
- Al apretar la membrana, el aire en la zona AB se comprime.
- Al estirar la membrana, el aire en la zona AB se vuelve menos denso, es decir, se rarifica.
Acústicas
Como una simple introducción a las ondas acústicas , consideremos una perturbación longitudinal en un gas confinado en una tuberia cilindrica. En equilibrio el gas permanece uniforme, con una presión constante.
Supongamos que ξ (x) es el desplazamiento del aire durante el paso de una onda sonora. Tomamos un elemento de volumen de aire de espesor dx, localizado entre dos planos de área A , perpendiculares a la dirección de propagación, situados en las coordenadas x y x + dx . El volumen antes de que pase la onda sonora es Adx = V.
Bajo estas condiciones se realiza un pequeño desplazamiento del gas, limitado por los planos A.
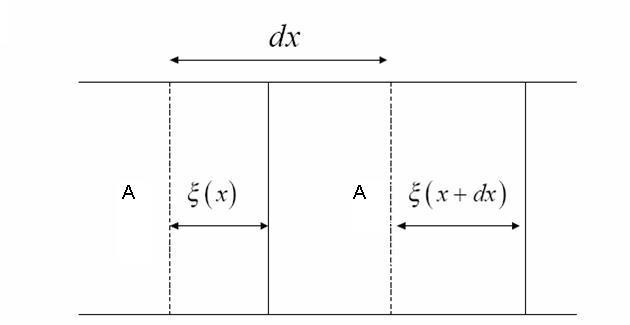
Al pasar la onda sonora, el plano izquierdo se desplaza una distancia ξ (x), y el plano derecho se desplaza una distancia
Por tanto, el incremento de volumen de este elemento será.
=
Estudiando el efecto de este incremento de volumen sobre la presión del aire y recordando que el aire, siendo un gas, se encuentra en equilibrio antes de que pase la onda sonora, nos fijamos en la compresibilidad del gas, la cual esta definida por :
=
Donde dP es la variación de la presión del aire respecto de su valor en el equilibrio.
En general, K es positiva demostrando que bajo una compresión ( dV < 0) , la presión del aire aumenta, y bajo una dilatación ( dV > 0 ) , la presión del aire disminuye.
Así del desplazamiento del aire en cada punto , tenemos que .
==
La fuerza generada por el desplazamiento del aire en el elemento seleccionado sobre sus alrededores es igual a la variación de la presión por el área normal A. Sobre el plano izquierdo, la fuerza es
==
y sobre el plano derecho
==
Aplicando la ecuación de Newton, encontramos la ecuación de movimiento para la masa de aire que se encuentra encerrada en nuestro elemento en cuestión.
=
siendo m ( x) la masa de aire del elemento
=
La aceleración del movimiento del aire será la segunda variación temporal de su desplazamiento respecto del equilibrio
=
Con esto, obtenemos
=
Hablando en general de la propagación de dos ondas, una onda de desplazamiento y una onda de presión. La velocidad de propagación de las ondas sonoras es
=
Referencias
Vibrations and Waves in Phisics, autor: Iain G. Main, editorial: Cambridge, tercera edición