Diferencia entre revisiones de «Ondas: observaciones»
Sin resumen de edición |
|||
| (No se muestran 73 ediciones intermedias de 13 usuarios) | |||
| Línea 1: | Línea 1: | ||
De lo que se observó en el laboratorio. | |||
De lo que se observó en el laboratorio | |||
== | == Reflexión == | ||
[[Archivo:Reflexion_luz.png|200px|thumb|left|texto descriptivo]] | [[Archivo:Reflexion_luz.png|200px|thumb|left|texto descriptivo]] | ||
Considérese un rayo de luz que se propaga a través de un medio homogéneo incide sobre la superficie | |||
de un segundo medio homogéneo, como resultado tenemos que parte de la luz es reflejada y la otra parte entra como un rayo refractado en el segundo medio, donde puede o no puede ser absorbido. | de un segundo medio homogéneo, como resultado tenemos que parte de la luz es reflejada y la otra parte entra como un rayo refractado en el segundo medio, donde puede o no puede ser absorbido. | ||
La cantidad de luz reflejada depende de la relación entre los índices de refracción de ambos medios. El plano de incidencia se define como el plano formado por el rayo incidente y la normal (es decir, la línea perpendicular a la superficie del medio) en el punto de incidencia, El ángulo de incidencia es el ángulo entre el rayo incidente y la normal. | La cantidad de luz reflejada depende de la relación entre los índices de refracción de ambos medios. El plano de incidencia se define como el plano formado por el rayo incidente y la normal (es decir, la línea perpendicular a la superficie del medio) en el punto de incidencia, El ángulo de incidencia es el ángulo entre el rayo incidente y la normal. | ||
| Línea 19: | Línea 18: | ||
== Refracción == | |||
Cuando el rayo de luz incidente encuentra otra frontera que conduce a otro medio, parte del rayo se transmite también al segundo medio. Este rayo se desvía en la barrera y se dice que se refracta. | |||
En el caso del prisma como el índice de refracción de una sustancia varía según la longitud de onda, un prisma puede separar las diferentes longitudes de onda contenidas en un haz incidente y formar un espectro. | |||
Podemos ilustrar a la refracción con un prisma en donde incidimos rayos de luz roja, verde y azul. Suponemos que la rapidez promedio de la luz roja en el vidrio es menor que en el aire, por lo que se refracta el rayo rojo. Al salir al aire vuelve a tener su rapidez original y viaja en la dirección indicada. La luz verde tarda más en atravesar el vidrio. Como su rapidez es menor se refracta como se indica. La luz azul atraviesa todavía con más lentitud; entonces podemos ver el cambio que presentan los rayos de luz con diferente rapidez. | |||
[[Archivo:Prisma de vidrio.JPG|200px|marco|centro|Prisma de vidrio en donde incidimos rayos de luz]] | |||
Ahora, sí solamente tenemos un "prisma de aire" y los rayos de luz, indicamos las trayectorias probables de los rayos, al atravesar el "prisma" y regresar al vidrio. | |||
[[Archivo:Prisma de aire.JPG|300px|marco|centro|posibles trayectorias de los rayos al atravesar el prisma]] | |||
Cuando se incidió la luz del láser al prisma, éste reflejo cierta cantidad de luz y otra la refractó, con un pequeño ángulo de inclinación, tomando como punto de referencia la normal a la superficie en el punto donde se tuvo contacto el haz. Para encontrar ese ángulo aplicamos la ley de Snell: | |||
<math>\mathbf{n_1}{sin\theta_{i1}}={n_2}{sin\theta_{t1}}</math> | |||
<math> \theta_{t1} =\arcsin(\frac{{n_1}{sin\theta_{i1}}}{n_2})</math> | |||
Lo que sucede del camino que va del prisma al aire: | |||
<math>\mathbf{n_3}{sin\theta_{i2}}={n_4}{sin\theta_{t2}}</math> | |||
<math> \theta_{t2} =\arcsin(\frac{{n_3}{sin\theta_{i2}}}{n_4})</math> | |||
pero sabemos que $n_1=n_3$, $n_2=n_4$, y que el ángulo transmitido en la primera parte es igual al ángulo incidente en la segunda parte del camino. | |||
<math> | <math> \theta_{t2} =\arcsin(\frac{{n_3}{sin\theta_{i2}}}{n_4})</math> | ||
<math> \theta_{t2}=\arcsin\left(\frac{n3}{n4}\sin\left(\arcsin\left(\frac{n1}{n2}\sin\theta_{i1}\right)\right)\right) </math> | |||
<math> | <math>\theta_{t2}=\theta_{i1}</math> | ||
Que en este caso parece el mismo ángulo con el cual incidió el láser por primera vez al prisma; ahora bien por la geometría del prisma tenemos que sumarle 45 grados al resultado obtenido para obtener el verdadero ángulo. | |||
[[ | ---- | ||
Aportación de: [[Usuario:Erika Fragoso Perez|Erika Fragoso Perez]] 18:09 30 mar 2012 (UTC) | |||
Ignacio Peralta Martínez | y [[Usuario:Ignacio Peralta Martínez|Ignacio Peralta Martínez]] 04:20 6 abr 2012 (UTC) | ||
---- | |||
== Interferencia == | == Interferencia == | ||
| Línea 67: | Línea 71: | ||
Con lo que respecta a interferencia en el laboratorio se observo el efecto de este | Con lo que respecta a interferencia en el laboratorio se observo el efecto de este fenómeno mediante el uso de un dispositivo conocido como interferómetro de Michelson. El diseño básico del instrumento se muestra en la figura (Fig. 3). Un haz de luz de una fuente ("S") cae sobre un vidrio ligeramente plateado ("A"), el cual divide el haz de luz en dos partes. Estos haz separados son reflejados de vuelta al vidrio ligeramente plateado ("A") por dos espejos ("C" y "D"). Usualmente una placa de compensación ("B") se inserta dentro del trayecto de una haz para que las dos trayectorias que toman los diferentes haces de luz incluyan y atraviesen el mismo grosor de espejo. El patrón de interferencia se observa en "E" | ||
--[[Usuario:Alejandro Angel Galvan Garcia|Alejandro Angel Galvan Garcia]] 21:57 26 mar 2012 (UTC) | ---- | ||
Aportación de: [[Usuario:Alejandro Angel Galvan Garcia|Alejandro Angel Galvan Garcia]] 21:57 26 mar 2012 (UTC) | |||
---- | |||
== Difracción == | |||
Difracción es el efecto que aparece sobre un haz de ondas cuando pasa a través de una rendija; la medida en que la difracción modifica la propagación ''rectilínea'' de las ondas depende del tamaño de la longitud de onda y de la abertura. | |||
Este efecto se puede observar de la siguiente manera: | |||
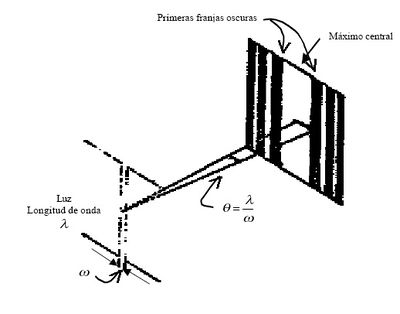
Difracción | [[Archivo:difraccion_fraunhofer.jpg|center|thumb|400x400px|Figura 4 - Difracción por una rendija]] | ||
Donde ω es la separación de la abertura de la rendija, λ se refiere a la longitud de onda y θ es la separación entre las franjas oscuras. Este fenómeno se puede observar colocando una pantalla blanca a una distancia ''d'' de la rendija, las franjas que se ven en la pantalla dependerán de que tan separadas estén las paredes de la abertura, si la abertura se va haciendo muy pequeña, es decir, disminuye, se observan las franjas muy cercanas unas de otras se deteriora su separación, hasta que pueda verse una linea recta oscura (θ decrece); si la distancia de la abertura va aumentando crece la separación de las franjas oscuras (θ aumenta). | Donde ω es la separación de la abertura de la rendija, λ se refiere a la longitud de onda y θ es la separación entre las franjas oscuras. Este fenómeno se puede observar colocando una pantalla blanca a una distancia ''d'' de la rendija, las franjas que se ven en la pantalla dependerán de que tan separadas estén las paredes de la abertura, si la abertura se va haciendo muy pequeña, es decir, disminuye, se observan las franjas muy cercanas unas de otras se deteriora su separación, hasta que pueda verse una linea recta oscura (θ decrece); si la distancia de la abertura va aumentando crece la separación de las franjas oscuras (θ aumenta). | ||
| Línea 90: | Línea 95: | ||
R.W. Ditchburn | R.W. Ditchburn | ||
Ed. Reverte, S.A | Ed. Reverte, S.A | ||
--[[Usuario:Heidi Isela Francisco Rodriguez|Heidi Isela Francisco Rodriguez]] 02:03 27 mar 2012 | |||
-- | |||
---- | |||
Aportación de: [[Usuario:Heidi Isela Francisco Rodriguez|Heidi Isela Francisco Rodriguez]] 02:03 27 mar 2012 | |||
---- | |||
[[categoría:Ondas]] | [[categoría:Ondas]] | ||
[[categoría:Cursos]] | [[categoría:Cursos]] | ||
== | == Reflexión total interna == | ||
Un rayo de luz propagándose en un medio con índice de refracción <math>\scriptstyle{n_1}</math> incidiendo con un ángulo <math>\scriptstyle{\theta_1}</math> sobre una superficie sobre un medio de índice <math>\scriptstyle{n_2}</math> con <math>\scriptstyle{n_1 > n_2}</math> puede reflejarse totalmente en el interior del medio de mayor índice de refracción. Este fenómeno se conoce como reflexión interna total o ángulo límite y se produce para ángulos de incidencia <math>\scriptstyle{\theta_1}</math> mayores que un valor crítico cuyo valor es: | Un rayo de luz propagándose en un medio con índice de refracción <math>\scriptstyle{n_1}</math> incidiendo con un ángulo <math>\scriptstyle{\theta_1}</math> sobre una superficie sobre un medio de índice <math>\scriptstyle{n_2}</math> con <math>\scriptstyle{n_1 > n_2}</math> puede reflejarse totalmente en el interior del medio de mayor índice de refracción. Este fenómeno se conoce como reflexión interna total o ángulo límite y se produce para ángulos de incidencia <math>\scriptstyle{\theta_1}</math> mayores que un valor crítico cuyo valor es: | ||
| Línea 102: | Línea 111: | ||
En la ley de Snell: | En la ley de Snell: | ||
:<math>n_1\sin\theta_1= n_2\sin\theta_2 \,</math> | :<math>n_1\sin\theta_1= n_2\sin\theta_2 \,</math> | ||
si <math>\scriptstyle{n_1\, > \,n_2}</math>, entonces <math>\scriptstyle{\theta_2 > \theta_1}</math>. Eso significa que cuando <math>\scriptstyle{\theta_1}</math> aumenta, <math>\scriptstyle{\theta_2}</math> llega a <math>\scriptstyle{\pi\over2}</math> radianes (90°) antes que <math>\scriptstyle{\theta_1}</math>. el rayo refractado (o transmitido) sale paralelo a la frontera. Si <math>\scriptstyle{\theta_1}</math> aumenta aún más, como <math>\scriptstyle{\theta_2}</math> no puede ser mayor que <math>\scriptstyle{\pi\over 2}</math>, no hay transmisión al otro medio y la luz se refleja totalmente. | si <math>\scriptstyle{n_1\, > \,n_2}</math>, entonces <math>\scriptstyle{\theta_2 > \theta_1}</math>. Eso significa que cuando <math>\scriptstyle{\theta_1}</math> aumenta, <math>\scriptstyle{\theta_2}</math> llega a <math>\scriptstyle{\pi\over2}</math> radianes (90°) antes que <math>\scriptstyle{\theta_1}</math>. el rayo refractado (o transmitido) sale paralelo a la frontera. Si <math>\scriptstyle{\theta_1}</math> aumenta aún más, como <math>\scriptstyle{\theta_2}</math> no puede ser mayor que <math>\scriptstyle{\pi\over 2}</math>, no hay transmisión al otro medio y la luz se refleja totalmente. | ||
| Línea 107: | Línea 117: | ||
La reflexión es realmente total (100%) y sin pérdidas. Es decir, mejor que los espejos metálicos (plata, aluminio) que solo reflejan 96% de la potencia luminosa incidente. | La reflexión es realmente total (100%) y sin pérdidas. Es decir, mejor que los espejos metálicos (plata, aluminio) que solo reflejan 96% de la potencia luminosa incidente. | ||
[[Archivo:Young.gif| | [[Archivo:Young.gif|center]] | ||
Un cálculo sencillo que podemos hacer en base a lo observado en el laboratorio es calcular el ángulo crítico, siendo vidrio el medio incidente y aire el medio donde se trasmitió el haz reflejado. Tómese <math>\scriptstyle{n_1 = 1.52}</math> para el vidrio y <math>\scriptstyle{n_2 = 1.00} </math> para el aire, entonces usando la relación encontrada arriba para el ángulo crítico tenemos que | Un cálculo sencillo que podemos hacer en base a lo observado en el laboratorio es calcular el ángulo crítico, siendo vidrio el medio incidente y aire el medio donde se trasmitió el haz reflejado. Tómese <math>\scriptstyle{n_1 = 1.52}</math> para el vidrio y <math>\scriptstyle{n_2 = 1.00} </math> para el aire, entonces usando la relación encontrada arriba para el ángulo crítico tenemos que | ||
| Línea 115: | Línea 125: | ||
<math>\theta_c = \arcsin(\frac{1.00}{1.52})\approx 0.718\ rad.</math> | <math>\theta_c = \arcsin(\frac{1.00}{1.52})\approx 0.718\ rad.</math> | ||
[[Archivo:Total_internal_reflection.jpg| | [[Archivo:Total_internal_reflection.jpg|center|400x300px|thumb|Reflexión total interna]] | ||
---- | |||
Aportación de: [[Usuario:Antonio de Jesus Jimenez Lopez|Antonio de Jesus Jimenez Lopez]] 23:18 2 abr 2012 (UTC) | |||
y [[Usuario:Roberto Verdel Aranda|Roberto Verdel Aranda]] 02:09 27 mar 2012 (UTC) | |||
---- | ---- | ||
== El efecto de moteado == | == El efecto de moteado == | ||
La apariencia granular al reflejarse sobre una superficie difusa es un fenómeno de la coherencia espacial de la luz del láser. Puede observarse fácilmente | La apariencia granular al reflejarse sobre una superficie difusa es un fenómeno de la coherencia espacial de la luz del láser. Puede observarse fácilmente expandiendo el haz, haciéndolo pasar a través de una lente simple y proyectándolo sobre una pared o sobre una hoja de papel. La interferencia de los frentes de onda dispersos produce una distribución de motas (speckles) de luz en el área iluminada. | ||
Si guiñamos un ojo los granos crecen de tamaño; si nos acercamos a la pantalla los granos se encogen, si nos quitamos las gafas, la distribución permanece en foco perfecto. Si el que está observando mueve su cabeza hacia la derecha y la distribución se mueve también a la derecha, entonces, significa que la persona es hipermétrope, en cambio, si la distribución se mueve a la izquierda entonces la persona es miope. | Si guiñamos un ojo los granos crecen de tamaño; si nos acercamos a la pantalla los granos se encogen, si nos quitamos las gafas, la distribución permanece en foco perfecto. Si el que está observando mueve su cabeza hacia la derecha y la distribución se mueve también a la derecha, entonces, significa que la persona es hipermétrope, en cambio, si la distribución se mueve a la izquierda entonces la persona es miope. | ||
--[[Usuario:Emmanuel Jairo Estrada Modesto|Emmanuel Jairo Estrada Modesto]] 06:33 27 mar 2012 (UTC) | |||
---- | |||
Aportación de: [[Usuario:Emmanuel Jairo Estrada Modesto|Emmanuel Jairo Estrada Modesto]] 06:33 27 mar 2012 (UTC) | |||
---- | |||
==Ángulo Crítico== | ==Ángulo Crítico== | ||
| Línea 132: | Línea 146: | ||
[[Archivo:AnguloCritico.jpg]] | [[Archivo:AnguloCritico.jpg]] | ||
--[[Usuario:Aurora Gonzalez|Aurora Gonzalez]] 03:05 27 mar 2012 (UTC) | ---- | ||
Aportación de: [[Usuario:Aurora Gonzalez|Aurora Gonzalez]] 03:05 27 mar 2012 (UTC) | |||
---- | |||
==Prismas Dispersivos== | ==Prismas Dispersivos== | ||
Pude observar en el laboratorio que cuando se le hacía incidir el haz al prisma, ésta mostraba | Pude observar en el laboratorio que cuando se le hacía incidir el haz al prisma, ésta mostraba | ||
un patrón muy peculiar,se veía como salía el haz después de haber sido desviado de su dirección original en un ángulo,llamado desviación angular. | un patrón muy peculiar,se veía como salía el haz después de haber sido desviado de su dirección original en un ángulo,llamado desviación angular.Los prismas sirven como sistema dispersivo;esto ocurre en muchos analizadores de espectro, es decir es capaz de separar, hasta cierto punto, las frecuencias constitutivas en un haz luminoso policromo. | ||
--[[Usuario:Espinoza Sosa Federico| | Otra función es la de producir un cambio en la orientación de la imagen o en la dirección de propagación del haz. | ||
---- | |||
Aportación de: [[Usuario:Federico Espinoza Sosa|Federico Espinoza Sosa]] 21:41 27 mar 2012 (UTC) | |||
---- | |||
==Pulsos Ultracortos== | |||
Los pulsos ultra cortos son a grandes rasgos pequeños trozos de un haz de luz, sin embargo ocurren en lapsos tan pequeños que es imposible detectarlos con nuestros propios ojos (receptores). por este motivo es necesario utilizar equipos sofisticados y sacar el mayor provecho de este fenómeno. | |||
Los pulsos Ultracortos son ideales para medir procesos atómicos que se encuentran en un lapso de tiempo de Picosegundos o Femtosegundos. | |||
El laboratorio de óptica cuántica de la UAM-I se observaron dos maneras para realizar pulsos de luz muy cortos. | |||
El primero de ellos: | |||
Se coloco un láser de color verde aproximadamente de 534 manómetros (longitud de onda) y se coloco un material, de manera muy precisa para que en el mínimo movimiento de esta pieza de un material en especial interfiriese con el haz, a este material se le aplico una corriente eléctrica, a lo que este respondió con vibraciones proporcionales a la antes mencionada. de esta manera se crearon pulsos mas y mas cortos hasta que fue imposible detectarlo con nuestros ojos y gracias a un receptor altamente sofisticado se nos convenció del hecho de ser pulsos cortos y no un haz de luz continuo | |||
En el segundo caso se efectúan sumas de ondas en un sistema mucho más complejo y el haz de luz ya no sale como tal, del láser sino como pulsos Ultracortos. (Observado en una plática diferente a la que fue presentada a todo el grupo). | |||
---- | |||
Aportación de: [[Usuario:José García Hernández|José García Hernández]] 07:57 30 mar 2012 (UTC) | |||
---- | |||
== Lentes == | |||
En cuanto a los lentes; podemos hablar de dos: el divergente y el convergente. | |||
Sabemos que los rayos se desvían, al atravesar un bloque de vidrio. | |||
En este arreglo de bloques de vidrio podemos ver como se desvían los rayos de luz al pasar por dicho arreglo. | |||
[[Archivo:LENTE CONVERGENTE.JPG|200px|marco|centro|Esquemas de lente convergente]] | |||
Este comportamiento es similar cuando en lugar de un arreglo tenemos un lente convergente. Porque los rayos convergen. | |||
El lente convergente se usa para corregir la hipermetropía. | |||
Por ultimo presentamos otro arreglo de bloques de vidrio y observaremos como se desvían los rayos de luz al pasar pór dicho arreglo. | |||
[[Archivo:LENTE DIVERGENTE.JPG|200px|marco|centro|Esquemas de lente divergente]] | |||
Este comportamiento es similar cuando en lugar de un arreglo como el anterior, tenemos un lente divergente. Porque los rayos divergen. | |||
El lente divergente se usa para arreglar la miopía. | |||
---- | |||
Aportación de: [[Usuario:Erika Fragoso Perez|Erika Fragoso Perez]] 18:37 30 mar 2012 (UTC) | |||
---- | |||
== El arco iris == | |||
El '''arco iris''' es una de las exhibiciones mas espectacular del espectro de la luz blanca en la naturaleza. Las condiciones requeridas para la aparición de este fenómeno, son que el Sol esté brillando en alguna parte del cielo y la lluvia esté cayendo en la parte opuesta. | |||
Dando uno la espalda al Sol, se pueden ver arcos de círculos, el arco iris primario brillante, y, a veces, el arco iris secundario, más débil, con los colores invertidos. Vistos desde alguna altura conveniente o desde un avión, estos arcos pueden formar círculos completos, cuyo centro común esta situado es la dirección de la sombra del observador. | |||
La teoría elemental del arco iris fue dada primero por Antonius de Demini en el año de 1611 y, posteriormente, desarrollado con mayor exactitud por Descartes. Las características generales de los arcos primario y secundario son explicadas satisfactoriamente al considerar solo la reflexión y la refracción de la luz por una gota esférica de lluvia. Para comprender como se produce el fenómeno, concentremos primero nuestra atención en una sola gota de lluvia. Se muestra un rayo de luz solar entrando entrando en una gota de lluvia por un punto A, cerca de su parte superior. En este punto, algo de luz se refleja, y el resto se refracta dentro de la esfera liquida. En esta primera refracción la luz se dispersa en sus colores espectrales, el color violeta es el que se desvía más, y el rojo el que se desvía menos. | |||
Llegando al lado opuesto de la gota, cada color es parcialmente refractado hacia afuera (dentro del aire), y en parte reflejado hacia atrás (dentro del liquido). Alcanzando la superficie en el límite inferior, cada uno de los colores es otra vez reflejado y refractado. Esta segunda refracción es muy similar a la de un prisma, en donde la refracción en la segunda superficie aumenta la dispersión ya producida en la primera. Ésta es la trayectoria de la luz en las miles de gotas que producen el brillante arco iris primario. | |||
Los arco iris existen debido al hecho de que las gotas de lluvia dispersan la luz preferentemente hacia ciertas direcciones. El efecto que produce esta dispersión es el de hacer que el cielo se vea más brillante en una determinada región. Este brillo lo conocemos como un arco iris, y sus colores son generados por los diferentes índices de refracción de los mismos. | |||
Una manera de entender la forma en la que se generan los arco iris es con un problema-ejemplo: | |||
'''''Si asumimos que el índice de refracción del agua es $\frac{4}{3}$ $(1.333)$ y que las gotas de lluvia son esféricas, el objetivo es demostrar que la ubicación del arco iris primario es de aproximadamente 42° por encima de la línea horizontal que separa al Sol y al observador. ¿Cuál sería el ángulo del segundo arco iris? Incluso los arco iris triples existen, aunque son difíciles de ver. ¿Dónde estaría el tercero?''''' | |||
'''Arco iris primario''' | |||
La dirección preferida que toma la luz cuando se dispersa depende de cuántas reflexiones el rayo de luz realiza dentro de la gota de lluvia. Primero consideremos el caso de una sola reflexión interna, como se muestra en la figura de abajo. El rayo de luz se refracta hacia el interior de la gota de lluvia, luego se refleja dentro de ella, y posteriormente se refracta de regreso al aire. Definamos entonces a β y ϕ como los ángulos mostrados en la figura; además se muestra lo que sería 2β y 2β-ϕ | |||
<center>[[Archivo:Arco_01.png]]</center> | |||
¿Cómo es ϕ en función de β? La expresión de Snell en los puntos de refracción nos da | |||
\begin{equation} | |||
\sin(2\beta -\phi)=\frac{4}{3} \sin\beta | |||
\label{1} | |||
\end{equation} | |||
Despejando a ϕ para dejarla en función de β resulta en | |||
\begin{equation} | |||
\phi = 2\beta - \arcsin(\frac{4}{3} \sin\beta) | |||
\label{2} | |||
\end{equation} | |||
La gráfica ϕ vs β se ve de la siguiente forma: | |||
<center>[[Archivo:Arco_02.png]]</center> | |||
'''Nota:''' Hay que resaltar que β no puede ser más grande que <math>\arcsin(4/3)\approx 48.6^o</math> porque esto resultaría en el $arc \sin$ de un número mayor que 1. 48.6° es el ángulo crítico para la interfase aire/agua. | |||
De la gráfica podemos observar que ϕ tiene un máximo de aproximadamente <math>\phi_{max} \approx 20^o</math> a un <math>\beta_{max}\approx 40^o</math>. Para ser más precisos, podemos calcular $\frac{\mathrm{d} \phi }{\mathrm{d} \beta}=0$. El resultado de esta operación es | |||
\begin{equation} | |||
0=2-\frac{\frac{4}{3}\cos\beta}{\sqrt{1-\frac{16}{9}\sin^2\beta}} | |||
\label{3} | |||
\end{equation} | |||
Elevando al cuadrado y utilizando la identidad <math>\cos^2\beta=1-\sin^2\beta</math> tenemos | |||
\begin{equation} | |||
\sin\beta_{max}=\sqrt{\frac{5}{12}} \qquad \Longrightarrow \qquad \beta_{max}\approx 40.2^o | |||
\label{4} | |||
\end{equation} | |||
Sustituyendo este valor en la ecuación (2) nos da como resultado | |||
\begin{equation} | |||
\phi_{max}\approx 21.0^o | |||
\label{5} | |||
\end{equation} | |||
La importancia de este máximo no radica en que es el valor más grande de ϕ, sino que la pendiente de ϕ(β) es igual a cero, lo cuál significa que hay muchos valores diferentes de β que producen esencialmente el mismo valor (<math>\approx 21^o</math>) de ϕ. La luz, entonces, se puede decir que se "enfoca" en el ángulo | |||
\begin{equation} | |||
2\phi_{max}\approx 42^o | |||
\end{equation} | |||
Por lo que el cielo parece ser más brillante a este ángulo (relativo a la línea horizontal entre el Sol y el observador). Esta brillantez es el arco iris que el observador ve. El razonamiento detrás de esto es tal vez más claro si se dibuja un diagrama con el ángulo de entrada de los rayos constante(que por cierto es el caso, pues todos los rayos del Sol son paralelos). Un dibujo más o menos bien hecho se muestra abajo. La línea gruesa es la trayectoria con el ángulo máximo de $2\phi$ de 42°. Se puede ver que los ángulos salientes se amontonan hacia este ángulo: | |||
<center>[[Archivo:Arco_03.png]]</center> | |||
Lo anterior explica por qué el arco iris se encuentra donde está, ¿pero por qué vemos colores diferentes? Los colores se crean por el hecho de que diferentes longitudes de onda en la luz tienen diferentes índices de refracción para la frontera entre el aire/agua. A un extremo del espectro de luz visible, la luz violeta tiene un índice de 1.344, y al otro extremo, la luz roja tiene un índice de 1.332. Si consideramos estos valores en los cálculos de arriba en lugar del "4/3", encontraremos que la luz violeta aparece a un ángulo de <math>2\phi_{v-max} \approx 40.5^o</math>, y la luz roja aparece a un ángulo <math>2\phi_{r-max}\approx 42.2^o</math>. Ya que el rojo aparece a un ángulo más grande, es ,por lo tanto, el color que se encuentra en la parte más alta del arco iris; el violeta está al fondo, y longitudes de onda intermedias se sitúan entre los dos. El que el rojo se encuentre en la cima puede ser explicado por el hecho de que 21° es el valor máximo de ϕ. | |||
Existe otra consecuencia para el hecho de que 21° es el valor de máximo para ϕ. Es posible para una gota de lluvia dispersar luz a valores de 2ϕ más pequeños que 42° (para una reflexión interna), pero imposible para ángulos más grandes. En consecuencia, la región en el cielo debajo de un arco iris parece ser más brillante que la región por encima del arco iris. Incluso si sólo los efectos de "enfoque" aparecen a la derecha de un arco iris, la simple dispersión de luz para valores de 2ϕ más pequeños que 42° hacen que este efecto de "más brillo" debajo del arco iris se lleve a cabo. | |||
Un arco iris es un poco más ancho que los aproximadamente 2° que encontramos, debido a que el Sol no es una fuente de luz puntual. El Sol delimita un ángulo de más o menos 0.5 grados, que agrega 0.5 grados al ancho del arco iris. Además, los colores del arco iris están algo difuminados en una escala de medio grado, por lo que de todas formas el arco iris no estaría tan definido si el Sol fuera una fuente de luz puntual. | |||
'''Arco iris secundario''' | |||
Ahora consideremos al arco iris secundario. Este arco iris se origina debido a que en la luz puede presentarse dos reflexiones dentro de la gota de lluvia antes de que se refracte de regreso hacia afuera. Este escenario se muestra abajo, donde se define β, los ángulos 180°-2β y 90°-β, y luego el ángulo 3β-90°. | |||
<center>[[Archivo:Arco_04.png]]</center> | |||
La expresión de Snell en los puntos de refracción nos da | |||
\begin{equation} | |||
\sin(3\beta - 90^o + \phi)=\frac{4}{3}\sin\beta | |||
\label{7} | |||
\end{equation} | |||
Despejando a ϕ de la ecuación tenemos | |||
\begin{equation} | |||
\phi=90^o -3\beta + \arcsin(\frac{4}{3}\sin\beta) | |||
\label{8} | |||
\end{equation} | |||
Haciendo la derivada para encontrar el valor extremo (que es un mínimo en esta ocasión) nos da | |||
\begin{equation} | |||
\sin\beta_{min}=\sqrt{\frac{65}{128}} \qquad \Longrightarrow \qquad \beta_{min}\approx 45.4^o | |||
\label{9} | |||
\end{equation} | |||
Sustituyendo este valor en la ecuación (8), tenemos | |||
\begin{equation} | |||
\phi_{min}\approx 25.4^o | |||
\label{10} | |||
\end{equation} | |||
Usando el mismo razonamiento que con el arco iris primario, vemos que la luz se enfoca a un ángulo de <math>2\phi_{max}\approx 51^o</math>, por lo que el cielo es más brillante a este ángulo. | |||
El hecho de que ϕ(β) tiene un mínimo en lugar de un máximo significa que el arco iris se invierte, con la luz violeta ahora en la parte más alta. Más preciso, si hacemos el cálculo con las ecuaciones de arriba pero ahora con los índices de refracción del rojo y el violeta en lugar del "4/3", encontraremos que la luz violeta aparece a un ángulo de 53.8°, y la luz roja aparece a un ángulo de 50.6°. El esparcimiento (ancho) aquí es un poco más grande que el del arco iris primario. | |||
El arco iris secundario es ligeramente más transparente que el primario por tres razones. La primera, que el mayor esparcimiento con respecto al primario significa que la luz se distribuye en un área más grande. La segunda, que cierta luz adicional se pierde cuando sucede la segunda reflexión interna. Y la tercera, el ángulo con respecto a la normal cuando el rayo de luz hace contacto con la gota de lluvia es mayor para el arco iris secundario; para el arco iris primario era <math>2\beta-\phi \approx 59^o</math>, mientras que para el arco iris secundario es <math>3\beta -90 ^{\circ}+\phi \approx 72 ^{\circ}</math>. | |||
<center>[[Archivo:Arco_05.png]]</center> | |||
---- | |||
Aportación de: Antonio de Jesus Jimenez Lopez|Antonio de Jesus Jimenez Lopez]] 19:29 3 abr 2012 (UTC) | |||
y [[Usuario:Roberto Martínez Sosa|Roberto Martínez Sosa]] 06:10 8 abr 2012 (UTC) | |||
---- | |||
==Laser Nd:YAG== | |||
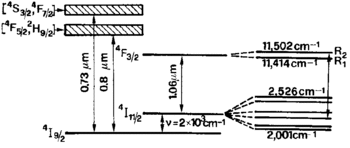
[[Archivo:Nivelesdeenergía.gif|thumb|350px|'''fig. 1''' Niveles de energía del Nd:YAG]] | |||
Los láseres de Nd:YAG (Y<sub>3</sub>Al<sub>5</sub>O<sub>12</sub>) son uno de los láseres de estado-solido mas usados del mundo, se llaman asi ya que utilizan un cristal de granate de itrio y aluminio (YAG) dopado con átomos de neodimio, debido a su versatilidad y por sus buenas propiedades térmicas y mecánicas, como es su alta conductividad térmica. Ademas el YAG arroja una estrecha linea de fluorescencia. | |||
Al ser un láser de estado solido se debe bombear, que pase de un nivel de energía mayor a uno menor el cristal de Nd:YAG como se muestra en la fig. 1, esta acción provoca que irradie un haz de 1064nm. el método de bombeo es irradiar el cristal normalmente con un diodo para producir un haz continuo o con una luz flash para un haz de pulsos con una longitud de onda de 0.73μm o de 0.8μm (ver fig. 1). Para poder amplificar el haz se usa un arreglo de espejos y lentes para re-inyectar una parte de la señal.Si bien un láser de Nd:YAG emite un haz infrarrojo (1064nm) el que se vio en el laboratorio era verde, esto sucede cuando al haz emitido se se le genera el segundo armónico con un cristal no lineal. | |||
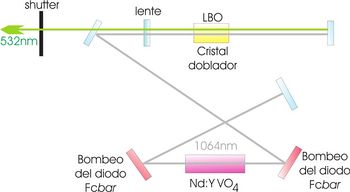
[[Archivo:LáserNd-YAG.jpg|thumb|350px|'''fig. 2''' Esquema de un láser Nd:YAG que emite a 532nm]] | |||
La generación del 2° armónico del láser Nd:YAG tiene como finalidad la producción de un nuevo láser cuya longitud de onda es la mitad de la del láser inicial como se observa en la fig. 2 que en este caso se usa un cristal no lineal de triborato de litio (LiB<sub>3</sub>O<sub>5</sub>) LBO para generar el segundo armónico del haz de 1064nm y generar un nuevo haz de 532nm, este método es el mas utilizado para hacer un láser verde en el mercado, incluyendo a los apuntadores láseres verdes. | |||
Esta generación del segundo armónico sucede cuando se le hace incidir al cristal no lineal el haz lo que provoca que gracias al campo eléctrico de la onda se genere un momento bipolar y cuando el campo eléctrico es muy grande las características no lineales del material cobran importancia y generan el armónico que en este caso el segundo. | |||
Entre los usos que se le da a este tipo de láseres sobresalen los oftalmológicos y los químicos y físico con el cual se pueden medir propiedades de un fenómeno de poca duración. | |||
---- | |||
Aportación de: [[Usuario:Julio Andrés Iglesias Martínez|Julio Andrés Iglesias Martínez]] 20:41 3 abr 2012 (UTC) | |||
---- | |||
Revisión actual - 02:01 5 jun 2023
De lo que se observó en el laboratorio.
Reflexión
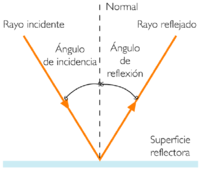
Considérese un rayo de luz que se propaga a través de un medio homogéneo incide sobre la superficie de un segundo medio homogéneo, como resultado tenemos que parte de la luz es reflejada y la otra parte entra como un rayo refractado en el segundo medio, donde puede o no puede ser absorbido. La cantidad de luz reflejada depende de la relación entre los índices de refracción de ambos medios. El plano de incidencia se define como el plano formado por el rayo incidente y la normal (es decir, la línea perpendicular a la superficie del medio) en el punto de incidencia, El ángulo de incidencia es el ángulo entre el rayo incidente y la normal.
De acuerdo a las leyes de reflexión:
Cada rayo de la onda incidente y el correspondiente rayo de la onda reflejada forman un plano perpendicular al plano de separación de los medios.
El ángulo que forma el rayo incidente con la recta normal a la frontera (ángulo de incidencia) es igual al ángulo de esta normal con el rayo reflejado (ángulo de reflexión)
En el laboratorio el medio considerado fue un prisma, un prisma es un objeto transparente con superficies planas y pulidas no paralelas
Refracción
Cuando el rayo de luz incidente encuentra otra frontera que conduce a otro medio, parte del rayo se transmite también al segundo medio. Este rayo se desvía en la barrera y se dice que se refracta. En el caso del prisma como el índice de refracción de una sustancia varía según la longitud de onda, un prisma puede separar las diferentes longitudes de onda contenidas en un haz incidente y formar un espectro.
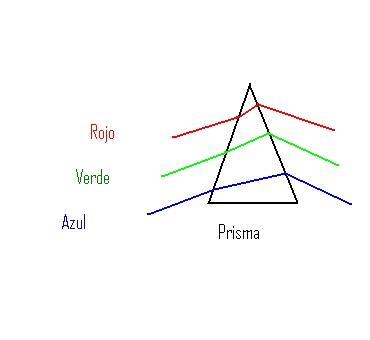
Podemos ilustrar a la refracción con un prisma en donde incidimos rayos de luz roja, verde y azul. Suponemos que la rapidez promedio de la luz roja en el vidrio es menor que en el aire, por lo que se refracta el rayo rojo. Al salir al aire vuelve a tener su rapidez original y viaja en la dirección indicada. La luz verde tarda más en atravesar el vidrio. Como su rapidez es menor se refracta como se indica. La luz azul atraviesa todavía con más lentitud; entonces podemos ver el cambio que presentan los rayos de luz con diferente rapidez.
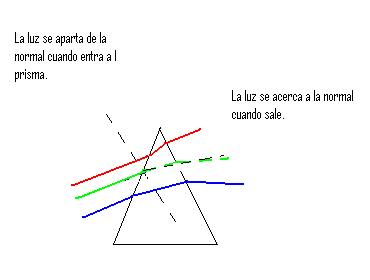
Ahora, sí solamente tenemos un "prisma de aire" y los rayos de luz, indicamos las trayectorias probables de los rayos, al atravesar el "prisma" y regresar al vidrio.
Cuando se incidió la luz del láser al prisma, éste reflejo cierta cantidad de luz y otra la refractó, con un pequeño ángulo de inclinación, tomando como punto de referencia la normal a la superficie en el punto donde se tuvo contacto el haz. Para encontrar ese ángulo aplicamos la ley de Snell:
Lo que sucede del camino que va del prisma al aire:
pero sabemos que $n_1=n_3$, $n_2=n_4$, y que el ángulo transmitido en la primera parte es igual al ángulo incidente en la segunda parte del camino.
Que en este caso parece el mismo ángulo con el cual incidió el láser por primera vez al prisma; ahora bien por la geometría del prisma tenemos que sumarle 45 grados al resultado obtenido para obtener el verdadero ángulo.
Aportación de: Erika Fragoso Perez 18:09 30 mar 2012 (UTC) y Ignacio Peralta Martínez 04:20 6 abr 2012 (UTC)
Interferencia
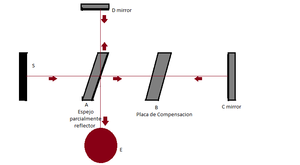
Con lo que respecta a interferencia en el laboratorio se observo el efecto de este fenómeno mediante el uso de un dispositivo conocido como interferómetro de Michelson. El diseño básico del instrumento se muestra en la figura (Fig. 3). Un haz de luz de una fuente ("S") cae sobre un vidrio ligeramente plateado ("A"), el cual divide el haz de luz en dos partes. Estos haz separados son reflejados de vuelta al vidrio ligeramente plateado ("A") por dos espejos ("C" y "D"). Usualmente una placa de compensación ("B") se inserta dentro del trayecto de una haz para que las dos trayectorias que toman los diferentes haces de luz incluyan y atraviesen el mismo grosor de espejo. El patrón de interferencia se observa en "E"
Aportación de: Alejandro Angel Galvan Garcia 21:57 26 mar 2012 (UTC)
Difracción
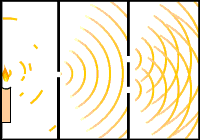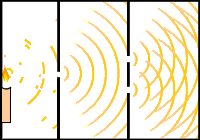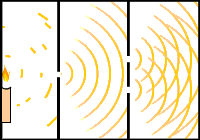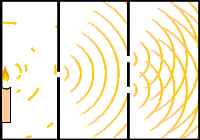
Difracción es el efecto que aparece sobre un haz de ondas cuando pasa a través de una rendija; la medida en que la difracción modifica la propagación rectilínea de las ondas depende del tamaño de la longitud de onda y de la abertura. Este efecto se puede observar de la siguiente manera:
Donde ω es la separación de la abertura de la rendija, λ se refiere a la longitud de onda y θ es la separación entre las franjas oscuras. Este fenómeno se puede observar colocando una pantalla blanca a una distancia d de la rendija, las franjas que se ven en la pantalla dependerán de que tan separadas estén las paredes de la abertura, si la abertura se va haciendo muy pequeña, es decir, disminuye, se observan las franjas muy cercanas unas de otras se deteriora su separación, hasta que pueda verse una linea recta oscura (θ decrece); si la distancia de la abertura va aumentando crece la separación de las franjas oscuras (θ aumenta).
ÓPTICA R.W. Ditchburn Ed. Reverte, S.A
Aportación de: Heidi Isela Francisco Rodriguez 02:03 27 mar 2012
Reflexión total interna
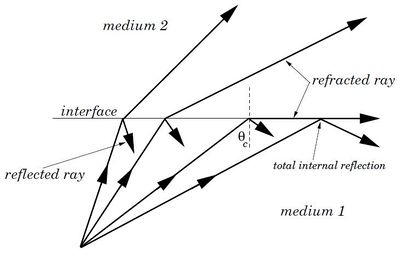
Un rayo de luz propagándose en un medio con índice de refracción incidiendo con un ángulo sobre una superficie sobre un medio de índice con puede reflejarse totalmente en el interior del medio de mayor índice de refracción. Este fenómeno se conoce como reflexión interna total o ángulo límite y se produce para ángulos de incidencia mayores que un valor crítico cuyo valor es:
En la ley de Snell:
si , entonces . Eso significa que cuando aumenta, llega a radianes (90°) antes que . el rayo refractado (o transmitido) sale paralelo a la frontera. Si aumenta aún más, como no puede ser mayor que , no hay transmisión al otro medio y la luz se refleja totalmente.
La reflexión es realmente total (100%) y sin pérdidas. Es decir, mejor que los espejos metálicos (plata, aluminio) que solo reflejan 96% de la potencia luminosa incidente.
Un cálculo sencillo que podemos hacer en base a lo observado en el laboratorio es calcular el ángulo crítico, siendo vidrio el medio incidente y aire el medio donde se trasmitió el haz reflejado. Tómese para el vidrio y para el aire, entonces usando la relación encontrada arriba para el ángulo crítico tenemos que
Aportación de: Antonio de Jesus Jimenez Lopez 23:18 2 abr 2012 (UTC) y Roberto Verdel Aranda 02:09 27 mar 2012 (UTC)
El efecto de moteado
La apariencia granular al reflejarse sobre una superficie difusa es un fenómeno de la coherencia espacial de la luz del láser. Puede observarse fácilmente expandiendo el haz, haciéndolo pasar a través de una lente simple y proyectándolo sobre una pared o sobre una hoja de papel. La interferencia de los frentes de onda dispersos produce una distribución de motas (speckles) de luz en el área iluminada. Si guiñamos un ojo los granos crecen de tamaño; si nos acercamos a la pantalla los granos se encogen, si nos quitamos las gafas, la distribución permanece en foco perfecto. Si el que está observando mueve su cabeza hacia la derecha y la distribución se mueve también a la derecha, entonces, significa que la persona es hipermétrope, en cambio, si la distribución se mueve a la izquierda entonces la persona es miope.
Aportación de: Emmanuel Jairo Estrada Modesto 06:33 27 mar 2012 (UTC)
Ángulo Crítico
Si un haz de luz pasa de un medio con índice de refracción menor a un medio con mayor índice de refracción, como en el caso cuando el haz pasa del aire al vidrio, el rayo refractado se curva acercándose hacia la normal, en el caso contrario el rayo se aleja de la normal. Entonces a un determinado ángulo de incidencia le corresponde un ángulo de refracción de 90° y el rayo refractado saldrá rasante a la superficie de separación de ambos miembros, a este ángulo se le llama ángulo critico o limite. Para los ángulos de incidencia mayores el rayo no será refractado, se produce una reflexión total interna.
Aportación de: Aurora Gonzalez 03:05 27 mar 2012 (UTC)
Prismas Dispersivos
Pude observar en el laboratorio que cuando se le hacía incidir el haz al prisma, ésta mostraba un patrón muy peculiar,se veía como salía el haz después de haber sido desviado de su dirección original en un ángulo,llamado desviación angular.Los prismas sirven como sistema dispersivo;esto ocurre en muchos analizadores de espectro, es decir es capaz de separar, hasta cierto punto, las frecuencias constitutivas en un haz luminoso policromo. Otra función es la de producir un cambio en la orientación de la imagen o en la dirección de propagación del haz.
Aportación de: Federico Espinoza Sosa 21:41 27 mar 2012 (UTC)
Pulsos Ultracortos
Los pulsos ultra cortos son a grandes rasgos pequeños trozos de un haz de luz, sin embargo ocurren en lapsos tan pequeños que es imposible detectarlos con nuestros propios ojos (receptores). por este motivo es necesario utilizar equipos sofisticados y sacar el mayor provecho de este fenómeno.
Los pulsos Ultracortos son ideales para medir procesos atómicos que se encuentran en un lapso de tiempo de Picosegundos o Femtosegundos.
El laboratorio de óptica cuántica de la UAM-I se observaron dos maneras para realizar pulsos de luz muy cortos. El primero de ellos:
Se coloco un láser de color verde aproximadamente de 534 manómetros (longitud de onda) y se coloco un material, de manera muy precisa para que en el mínimo movimiento de esta pieza de un material en especial interfiriese con el haz, a este material se le aplico una corriente eléctrica, a lo que este respondió con vibraciones proporcionales a la antes mencionada. de esta manera se crearon pulsos mas y mas cortos hasta que fue imposible detectarlo con nuestros ojos y gracias a un receptor altamente sofisticado se nos convenció del hecho de ser pulsos cortos y no un haz de luz continuo
En el segundo caso se efectúan sumas de ondas en un sistema mucho más complejo y el haz de luz ya no sale como tal, del láser sino como pulsos Ultracortos. (Observado en una plática diferente a la que fue presentada a todo el grupo).
Aportación de: José García Hernández 07:57 30 mar 2012 (UTC)
Lentes
En cuanto a los lentes; podemos hablar de dos: el divergente y el convergente.
Sabemos que los rayos se desvían, al atravesar un bloque de vidrio.
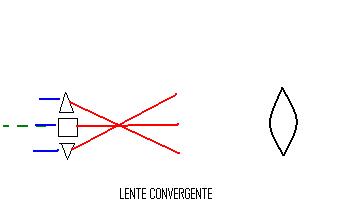
En este arreglo de bloques de vidrio podemos ver como se desvían los rayos de luz al pasar por dicho arreglo.
Este comportamiento es similar cuando en lugar de un arreglo tenemos un lente convergente. Porque los rayos convergen.
El lente convergente se usa para corregir la hipermetropía.
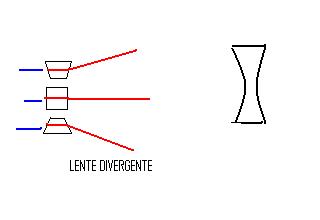
Por ultimo presentamos otro arreglo de bloques de vidrio y observaremos como se desvían los rayos de luz al pasar pór dicho arreglo.
Este comportamiento es similar cuando en lugar de un arreglo como el anterior, tenemos un lente divergente. Porque los rayos divergen.
El lente divergente se usa para arreglar la miopía.
Aportación de: Erika Fragoso Perez 18:37 30 mar 2012 (UTC)
El arco iris
El arco iris es una de las exhibiciones mas espectacular del espectro de la luz blanca en la naturaleza. Las condiciones requeridas para la aparición de este fenómeno, son que el Sol esté brillando en alguna parte del cielo y la lluvia esté cayendo en la parte opuesta.
Dando uno la espalda al Sol, se pueden ver arcos de círculos, el arco iris primario brillante, y, a veces, el arco iris secundario, más débil, con los colores invertidos. Vistos desde alguna altura conveniente o desde un avión, estos arcos pueden formar círculos completos, cuyo centro común esta situado es la dirección de la sombra del observador.
La teoría elemental del arco iris fue dada primero por Antonius de Demini en el año de 1611 y, posteriormente, desarrollado con mayor exactitud por Descartes. Las características generales de los arcos primario y secundario son explicadas satisfactoriamente al considerar solo la reflexión y la refracción de la luz por una gota esférica de lluvia. Para comprender como se produce el fenómeno, concentremos primero nuestra atención en una sola gota de lluvia. Se muestra un rayo de luz solar entrando entrando en una gota de lluvia por un punto A, cerca de su parte superior. En este punto, algo de luz se refleja, y el resto se refracta dentro de la esfera liquida. En esta primera refracción la luz se dispersa en sus colores espectrales, el color violeta es el que se desvía más, y el rojo el que se desvía menos.
Llegando al lado opuesto de la gota, cada color es parcialmente refractado hacia afuera (dentro del aire), y en parte reflejado hacia atrás (dentro del liquido). Alcanzando la superficie en el límite inferior, cada uno de los colores es otra vez reflejado y refractado. Esta segunda refracción es muy similar a la de un prisma, en donde la refracción en la segunda superficie aumenta la dispersión ya producida en la primera. Ésta es la trayectoria de la luz en las miles de gotas que producen el brillante arco iris primario.
Los arco iris existen debido al hecho de que las gotas de lluvia dispersan la luz preferentemente hacia ciertas direcciones. El efecto que produce esta dispersión es el de hacer que el cielo se vea más brillante en una determinada región. Este brillo lo conocemos como un arco iris, y sus colores son generados por los diferentes índices de refracción de los mismos.
Una manera de entender la forma en la que se generan los arco iris es con un problema-ejemplo:
Si asumimos que el índice de refracción del agua es $\frac{4}{3}$ $(1.333)$ y que las gotas de lluvia son esféricas, el objetivo es demostrar que la ubicación del arco iris primario es de aproximadamente 42° por encima de la línea horizontal que separa al Sol y al observador. ¿Cuál sería el ángulo del segundo arco iris? Incluso los arco iris triples existen, aunque son difíciles de ver. ¿Dónde estaría el tercero?
Arco iris primario
La dirección preferida que toma la luz cuando se dispersa depende de cuántas reflexiones el rayo de luz realiza dentro de la gota de lluvia. Primero consideremos el caso de una sola reflexión interna, como se muestra en la figura de abajo. El rayo de luz se refracta hacia el interior de la gota de lluvia, luego se refleja dentro de ella, y posteriormente se refracta de regreso al aire. Definamos entonces a β y ϕ como los ángulos mostrados en la figura; además se muestra lo que sería 2β y 2β-ϕ
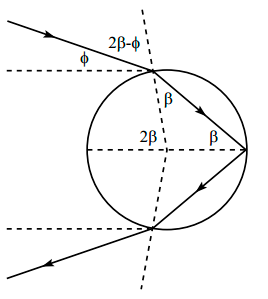
¿Cómo es ϕ en función de β? La expresión de Snell en los puntos de refracción nos da
\begin{equation} \sin(2\beta -\phi)=\frac{4}{3} \sin\beta \label{1} \end{equation}
Despejando a ϕ para dejarla en función de β resulta en
\begin{equation} \phi = 2\beta - \arcsin(\frac{4}{3} \sin\beta) \label{2} \end{equation}
La gráfica ϕ vs β se ve de la siguiente forma:
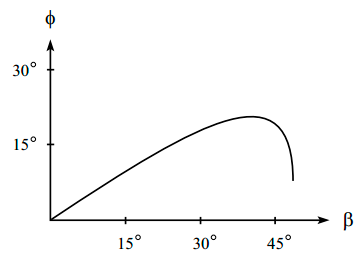
Nota: Hay que resaltar que β no puede ser más grande que porque esto resultaría en el $arc \sin$ de un número mayor que 1. 48.6° es el ángulo crítico para la interfase aire/agua.
De la gráfica podemos observar que ϕ tiene un máximo de aproximadamente a un . Para ser más precisos, podemos calcular $\frac{\mathrm{d} \phi }{\mathrm{d} \beta}=0$. El resultado de esta operación es
\begin{equation} 0=2-\frac{\frac{4}{3}\cos\beta}{\sqrt{1-\frac{16}{9}\sin^2\beta}} \label{3} \end{equation}
Elevando al cuadrado y utilizando la identidad tenemos
\begin{equation} \sin\beta_{max}=\sqrt{\frac{5}{12}} \qquad \Longrightarrow \qquad \beta_{max}\approx 40.2^o \label{4} \end{equation}
Sustituyendo este valor en la ecuación (2) nos da como resultado
\begin{equation} \phi_{max}\approx 21.0^o \label{5} \end{equation}
La importancia de este máximo no radica en que es el valor más grande de ϕ, sino que la pendiente de ϕ(β) es igual a cero, lo cuál significa que hay muchos valores diferentes de β que producen esencialmente el mismo valor () de ϕ. La luz, entonces, se puede decir que se "enfoca" en el ángulo
\begin{equation}
2\phi_{max}\approx 42^o
\end{equation}
Por lo que el cielo parece ser más brillante a este ángulo (relativo a la línea horizontal entre el Sol y el observador). Esta brillantez es el arco iris que el observador ve. El razonamiento detrás de esto es tal vez más claro si se dibuja un diagrama con el ángulo de entrada de los rayos constante(que por cierto es el caso, pues todos los rayos del Sol son paralelos). Un dibujo más o menos bien hecho se muestra abajo. La línea gruesa es la trayectoria con el ángulo máximo de $2\phi$ de 42°. Se puede ver que los ángulos salientes se amontonan hacia este ángulo:
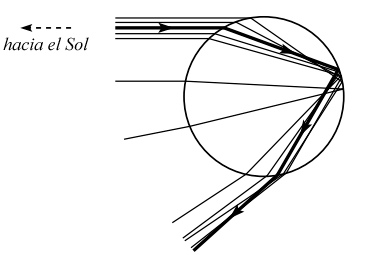
Lo anterior explica por qué el arco iris se encuentra donde está, ¿pero por qué vemos colores diferentes? Los colores se crean por el hecho de que diferentes longitudes de onda en la luz tienen diferentes índices de refracción para la frontera entre el aire/agua. A un extremo del espectro de luz visible, la luz violeta tiene un índice de 1.344, y al otro extremo, la luz roja tiene un índice de 1.332. Si consideramos estos valores en los cálculos de arriba en lugar del "4/3", encontraremos que la luz violeta aparece a un ángulo de , y la luz roja aparece a un ángulo . Ya que el rojo aparece a un ángulo más grande, es ,por lo tanto, el color que se encuentra en la parte más alta del arco iris; el violeta está al fondo, y longitudes de onda intermedias se sitúan entre los dos. El que el rojo se encuentre en la cima puede ser explicado por el hecho de que 21° es el valor máximo de ϕ.
Existe otra consecuencia para el hecho de que 21° es el valor de máximo para ϕ. Es posible para una gota de lluvia dispersar luz a valores de 2ϕ más pequeños que 42° (para una reflexión interna), pero imposible para ángulos más grandes. En consecuencia, la región en el cielo debajo de un arco iris parece ser más brillante que la región por encima del arco iris. Incluso si sólo los efectos de "enfoque" aparecen a la derecha de un arco iris, la simple dispersión de luz para valores de 2ϕ más pequeños que 42° hacen que este efecto de "más brillo" debajo del arco iris se lleve a cabo.
Un arco iris es un poco más ancho que los aproximadamente 2° que encontramos, debido a que el Sol no es una fuente de luz puntual. El Sol delimita un ángulo de más o menos 0.5 grados, que agrega 0.5 grados al ancho del arco iris. Además, los colores del arco iris están algo difuminados en una escala de medio grado, por lo que de todas formas el arco iris no estaría tan definido si el Sol fuera una fuente de luz puntual.
Arco iris secundario
Ahora consideremos al arco iris secundario. Este arco iris se origina debido a que en la luz puede presentarse dos reflexiones dentro de la gota de lluvia antes de que se refracte de regreso hacia afuera. Este escenario se muestra abajo, donde se define β, los ángulos 180°-2β y 90°-β, y luego el ángulo 3β-90°.
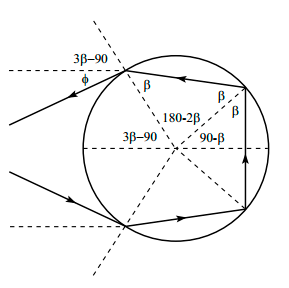
La expresión de Snell en los puntos de refracción nos da
\begin{equation}
\sin(3\beta - 90^o + \phi)=\frac{4}{3}\sin\beta
\label{7}
\end{equation}
Despejando a ϕ de la ecuación tenemos
\begin{equation} \phi=90^o -3\beta + \arcsin(\frac{4}{3}\sin\beta) \label{8} \end{equation}
Haciendo la derivada para encontrar el valor extremo (que es un mínimo en esta ocasión) nos da
\begin{equation} \sin\beta_{min}=\sqrt{\frac{65}{128}} \qquad \Longrightarrow \qquad \beta_{min}\approx 45.4^o \label{9} \end{equation}
Sustituyendo este valor en la ecuación (8), tenemos
\begin{equation} \phi_{min}\approx 25.4^o \label{10} \end{equation}
Usando el mismo razonamiento que con el arco iris primario, vemos que la luz se enfoca a un ángulo de , por lo que el cielo es más brillante a este ángulo.
El hecho de que ϕ(β) tiene un mínimo en lugar de un máximo significa que el arco iris se invierte, con la luz violeta ahora en la parte más alta. Más preciso, si hacemos el cálculo con las ecuaciones de arriba pero ahora con los índices de refracción del rojo y el violeta en lugar del "4/3", encontraremos que la luz violeta aparece a un ángulo de 53.8°, y la luz roja aparece a un ángulo de 50.6°. El esparcimiento (ancho) aquí es un poco más grande que el del arco iris primario.
El arco iris secundario es ligeramente más transparente que el primario por tres razones. La primera, que el mayor esparcimiento con respecto al primario significa que la luz se distribuye en un área más grande. La segunda, que cierta luz adicional se pierde cuando sucede la segunda reflexión interna. Y la tercera, el ángulo con respecto a la normal cuando el rayo de luz hace contacto con la gota de lluvia es mayor para el arco iris secundario; para el arco iris primario era , mientras que para el arco iris secundario es .
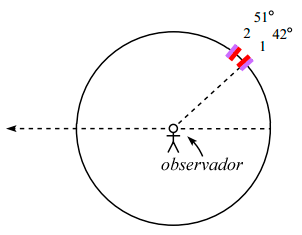
Aportación de: Antonio de Jesus Jimenez Lopez|Antonio de Jesus Jimenez Lopez]] 19:29 3 abr 2012 (UTC) y Roberto Martínez Sosa 06:10 8 abr 2012 (UTC)
Laser Nd:YAG
Los láseres de Nd:YAG (Y3Al5O12) son uno de los láseres de estado-solido mas usados del mundo, se llaman asi ya que utilizan un cristal de granate de itrio y aluminio (YAG) dopado con átomos de neodimio, debido a su versatilidad y por sus buenas propiedades térmicas y mecánicas, como es su alta conductividad térmica. Ademas el YAG arroja una estrecha linea de fluorescencia.
Al ser un láser de estado solido se debe bombear, que pase de un nivel de energía mayor a uno menor el cristal de Nd:YAG como se muestra en la fig. 1, esta acción provoca que irradie un haz de 1064nm. el método de bombeo es irradiar el cristal normalmente con un diodo para producir un haz continuo o con una luz flash para un haz de pulsos con una longitud de onda de 0.73μm o de 0.8μm (ver fig. 1). Para poder amplificar el haz se usa un arreglo de espejos y lentes para re-inyectar una parte de la señal.Si bien un láser de Nd:YAG emite un haz infrarrojo (1064nm) el que se vio en el laboratorio era verde, esto sucede cuando al haz emitido se se le genera el segundo armónico con un cristal no lineal.
La generación del 2° armónico del láser Nd:YAG tiene como finalidad la producción de un nuevo láser cuya longitud de onda es la mitad de la del láser inicial como se observa en la fig. 2 que en este caso se usa un cristal no lineal de triborato de litio (LiB3O5) LBO para generar el segundo armónico del haz de 1064nm y generar un nuevo haz de 532nm, este método es el mas utilizado para hacer un láser verde en el mercado, incluyendo a los apuntadores láseres verdes.
Esta generación del segundo armónico sucede cuando se le hace incidir al cristal no lineal el haz lo que provoca que gracias al campo eléctrico de la onda se genere un momento bipolar y cuando el campo eléctrico es muy grande las características no lineales del material cobran importancia y generan el armónico que en este caso el segundo.
Entre los usos que se le da a este tipo de láseres sobresalen los oftalmológicos y los químicos y físico con el cual se pueden medir propiedades de un fenómeno de poca duración.
Aportación de: Julio Andrés Iglesias Martínez 20:41 3 abr 2012 (UTC)