Ondas: Gaussianas

Haces Gaussianos

Un haz gaussiano es representado por

$a\left(x,y,z\right)=\left({\frac {2}{\pi }}\right)^{1/2}{\frac {q_{0}}{w_{0}q\left(z\right)}}e^{ikz+ik{\frac {x^{2}+y^{2}}{2q\left(z\right)}}},$

donde el radio complejo de curvatura esta dado por

${\frac {1}{q\left(z\right)}}\equiv {\frac {1}{R\left(z\right)}}+i{\frac {\lambda }{\pi w^{2}\left(z\right)}}.$

Esta expresión es solución de la ecuación paraxial. La amplitud del campo es entonces

$u\left({x,y,z}\right)=\left({\frac {2}{\pi }}\right)^{1/2}{\frac {1}{w\left(z\right)}}e^{ikz+i\psi \left(z\right)}e^{ik{\frac {x^{2}+y^{2}}{2R\left(z\right)}}-{\frac {x^{2}+y^{2}}{w^{2}\left(z\right)}}}$

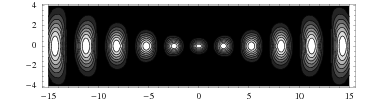
En espacio libre

$q=z+q_{0}=z+iz_{R}$

donde

$q_{0}=i{\frac {\pi w_{0}^{2}}{\lambda }}$

y la distancia de Rayleigh es

$z_{R}={\frac {\pi w_{0}^{2}}{\lambda }}$

el ancho del haz es:

$w=w_{0}{\sqrt {1+\left({\frac {z}{z_{R}}}\right)^{2}}}$

su radio de curvatura es:

$R=z+{\frac {z_{R}^{2}}{z}}$

y la fase añadida es

$\psi =\arctan \left({\frac {z}{z_{R}}}\right)$

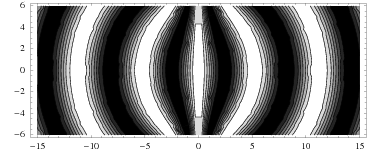
La potencia del haz en función del radio $a$ de la apertura:

$P=1-e^{-{\frac {2a^{2}}{w^{2}}}}$

La divergencia del haz es:

$\theta _{1/e}={\frac {\lambda }{\pi w_{0}}}$

Para una lente de distancia focal $f$, el diámetro en el foco

es:

$d_{0}\approx {\frac {2f\lambda }{D}}$

donde $D$ es el diámetro de haz a la entrada de la lente.

plano de máxima curvatura

Para determinar la zona en donde la curvatura de la onda es más severa nos valemos de la expresión que define el radio de curvatura

$R(z)=(z-z_{0})+{\frac {z_{R}^{2}}{(z-z_{0})}}.$

Para encontrar el radio de máxima curvatura derivo la función anterior y posteriormente la igualo a cero

${\frac {dR(z)}{dz}}=1-{\frac {z_{R}^{2}}{(z-z_{0})^{2}}}.$

Igualando a cero

$1-{\frac {z_{R}^{2}}{(z-z_{0})^{2}}}=0.$

Lo cual después de algunos despejes

$z_{R}^{2}=(z-z_{0})^{2}.$

En esta última expresión tenemos que tener cuidado al despejar $z\$ ya que nos encontraremos con dos raíces una positiva y una negativa i.e.

$\pm {\sqrt {z_{R}^{2}}}=z-z_{0}.$

Con un poco mas de algebra encontramos las soluciones, la primera es.

$z_{1}^{}=z_{0}+z_{R}.$

Y la segunda

$z_{2}^{}=z_{0}-z_{R}.$

Era de esperarse un resultado así de simétrico puesto que la onda se propaga de igual forma en ambas direcciones, cabe señalar que la curva es más severa cuando estamos a una distancia de Rayleigh $z_{R}\$.

references

--Mfg 23:11 22 oct 2007 (CDT)