Ondas: 3 dimensiones
Ondas en 3 dimensiones
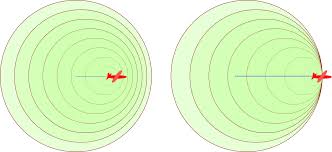
Las ondas tridimensionales son ondas que se propagan en tres dimensiones, se conocen también como ondas esféricas, porque sus frentes de ondas son esferas concéntricas que salen de la fuente de perturbación expandiéndose en todas direcciones (3D). Ejemplos de ondas tridimensionales son: las ondas sonoras y las ondas electromagnéticas
Cuando se propaga una onda en un espacio de tres dimensiones, la fase es una función continua de $x,y,z,t$. en un instante dado cualquiera , la fase tiene el mismo valor en todos los puntos de ciertas superficies a las que se da el nombre de superficie de onda. Vienen definidas por la relación.
Donde es una función de las coordenadas espaciales y es el valor de correspondiente a una superficie particular en el instante
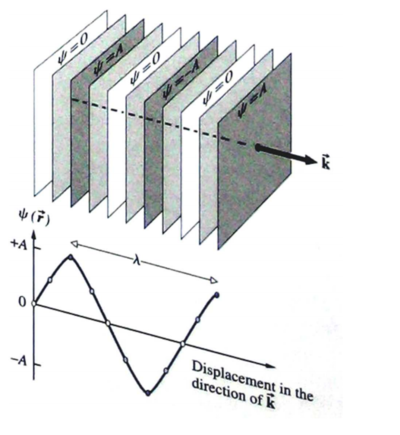
En general, las superficies de onda constituyen una familia de superficies en la que es el parámetro variable que selecciona a un miembro particular de la familia. Las superficies de onda pueden constituir una familia de esféras concéntricas o una familia de planos paralelos y también puede adoptar otras formas. Las ondas se denominan ondas esféricas,ondas planas, etc., según sea la forma de las superficies de onda. Cuando avanzan las ondas por una región que hasta entonces no había sido perturbada, la superficie correspondiente a la primera cresta de denomina frente de onda.
Ecuación de onda en tres dimensiones
La función de onda dada por la ecuación (14) en el tema Ondas: planas es una solución partícular de de la ecuación diferencial en tres dimensiones, calculamos entonces las derivadas parciales de la ecuación (14) antes mencionada
\begin{equation}
\frac{\partial^{2}\psi}{\partial{x^{2}}}=-\alpha^{2}k^{2}\psi
\end{equation}
\begin{equation} \frac{\partial^{2}\psi}{\partial{y^{2}}}=-\beta^{2}k^{2}\psi \end{equation}
\begin{equation} \frac{\partial^{2}\psi}{\partial{z^{2}}}=-\gamma^{2}k^{2}\psi \end{equation}
\begin{equation} \frac{\partial^{2}\psi}{\partial{t^{2}}}=-\omega^{2}\psi \end{equation}
Sumando las tres derivadas parciales y usando el hecho de que , obtenemos
\begin{equation} \frac{\partial^{2}\psi}{\partial{x^{2}}}+\frac{\partial^{2}\psi}{\partial{y^{2}}}+\frac{\partial^{2}\psi}{\partial{z^{2}}}=-k^{2}\psi \end{equation}
Combinando esto con la derivada del tiempo, ecuación 4 y recordando que , llegamos a
\begin{equation} \frac{\partial^{2}\psi}{\partial{x^{2}}}+\frac{\partial^{2}\psi}{\partial{y^{2}}}+\frac{\partial^{2}\psi}{\partial{z^{2}}}=\frac{1}{v^{2}}\frac{\partial^{2}\psi}{\partial{t^{2}}} \end{equation}
que es la ecuación diferencial de onda tridimencional. Obsérvese que x, y, y z aparecen simétricamente y que la forma es precisamente la que uno esperaría de la generalización de la ecuación unidimensional que se puede ver en Ondas: ecuación de onda
La ecuación 6 se escribe,por lo general, de una forma más concisa introduciendo el operador Laplaciano
\begin{equation} \nabla^{2}=\frac{\partial^{2}}{\partial{x^{2}}}+\frac{\partial^{2}}{\partial{y^{2}}}+\frac{\partial^{2}}{\partial{z^{2}}} \end{equation}
Por tanto, la ecuación de onda se puede escribir de forma compacta en términos del laplaciano como:
\begin{equation} \nabla^{2}\psi=\frac{1}{v^{2}}\frac{\partial^{2}{\psi}}{\partial{t^{2}}} \end{equation}
Soluciones a la ecuación de onda tridimensional
Las soluciones de la ecuación de onda tridimensional (ecuación 8) no son más difíciles de conseguir que los de la ecuación de onda unidimensional. De hecho, si buscamos soluciones que sean independientes de $y$ y $z$, recuperamos las soluciones obtenidas para la ecuación unidimensional. Entonces, por ejemplo, la solución (compleja) de onda
\begin{equation} \psi(x,y=0,z=0,t)= Ae^{ik(x-vt)}. \end{equation} La cual es independiente de $y$ y $z$, y es una onda desplazándose positivamente en $x$. Ahora veamos su solución general ya dependiente de las 4 variables:
\begin{equation} \psi(\vec{r},t)=Ae^{i(\vec{k}\cdot\vec{r}-wt)};\thinspace con \thinspace \vec{r}=(x,y,z). \end{equation}
Se puede ver que tiene la misma forma que la ecuación de onda en una dimensión. Ahora vamos a encontrar $w$ y $k$ y para ello redefinimos las siguientes ecuaciones:
\[ \frac{\partial^{2}\psi}{\partial{x^{2}}}=-\alpha^{2}k^{2}\psi=-k_x^2\psi. \]
\[ \frac{\partial^{2}\psi}{\partial{y^{2}}}=-\beta^{2}k^{2}\psi=-k_y^2\psi. \]
\[ \frac{\partial^{2}\psi}{\partial{z^{2}}}=-\gamma^{2}k^{2}\psi=-k_z^2\psi. \]
\[ \frac{\partial^{2}\psi}{\partial{t^{2}}}=-\omega^{2}\psi. \]
Entonces la ecuación de onda es:
\[ \nabla^{2}\psi=\frac{1}{v^{2}}\frac{\partial^{2}{\psi}}{\partial{t^{2}}}, \] \begin{equation} -(k_x^2+k_y^2+k_z^2)\psi(\vec{r},t)=-\frac{w^2}{v^2}\psi(\vec{r},t). \end{equation}
despejando $w$
\[ -(k_x^2+k_y^2+k_z^2)=-\frac{w^2}{v^2}, \]
\[ w^2=v^2(k_x^2+k_y^2+k_z^2), \]
\begin{equation} w=v\sqrt{k_x^2+k_y^2+k_z^2}. \end{equation}
y definiendo $k$ como $\vec{k}=(k_x,k_y,k_z)$, entonces $|\vec{k}|=\sqrt{k_x^2+k_y^2+k_z^2}$ por lo que $w$ es:
\begin{equation} w=v|\vec{k}|. \end{equation}
Por lo tanto su solución es:
\begin{equation} \psi(x,y,z,t)=Ae^{i(k_xx+k_yy+k_zz-wt)}. \end{equation}
Como es habitual, se pueden obtener soluciones reales separando las partes reales e imaginarias. Para verificar que (10) satisface la ecuación de onda, se puede simplemente sustituir (10) en (8) y se comprueba que si se cumple la ecuación de onda, la relación de dispersión (13) hace que eso suceda.
Alternativamente, puede verificar que (10) (con (13)) satisface la ecuación de onda utilizando el siguiente argumento (que es un poco complicado): El producto escalar $\vec{k} \cdot \vec{r}$ es un escalar que se define geométricamente, es decir, es independientemente de la orientación de los ejes $(x,y,z)$. Asimismo, el laplaciano es el mismo sin importar el orientación de estos ejes. Para que podamos elegir nuestros ejes de la forma que se desee (la ecuación de onda no depende de tales elecciones).
Para un vector dado $\vec{k}$, supongamos que elegimos el eje $x$ en la dirección de $\vec{k}$, entonces $\vec{k} \cdot \vec{x}=kx$, por lo que $\psi(x, t)$ toma la forma de la solución (compleja) a la ecuación de onda en una dimensión. Ya hemos encontrado que si $\psi = \psi(x, t)$ la ecuación de onda en tres dimensiones se reduce a la ecuación de onda en una dimensión. Por lo tanto, (10) resuelve (8) ya que se ha reducido la situación al caso unidimensional. Las soluciones a la ecuación de onda de la forma (10) se llaman ondas planas porque en cualquier tiempo daso, se ven iguales a medida que uno se mueve a lo largo de cualquier plano, ya que $\vec{k}\cdot\vec{r}= constante$.
Hay que tomar en cuenta la relación entre la frecuencia y la longitud de onda asociada con la onda plana (10): \begin{equation} w=|\vec{k}|v= \frac{2\pi}{\lambda}v. \end{equation}
Ésta es la relación de dispersión para ondas planas en tres dimensiones. Podemos ver esta restricción como si fijáramos la frecuencia $w$ en términos de la magnitud de $|\vec{k}|$ pero dejando el vector de onda $\vec{k}$ libre. De hecho, la relación de dispersión, $w = |k|v$ todavía se mantiene en el entorno tridimensional, siempre que interpretemos $|k|$ como la magnitud del vector de onda. Como veremos, cada onda plana que aparece en la descomposición de Fourier de la solución general de (8) es, matemáticamente, sólo una solución sinusoidal compleja de una ecuación de onda unidimensional.
Desafortunadamente, no es tan fácil escribir una fórmula simple para la solución general a la ecuación de onda tridimensional, como si lo es en el caso unidimensional, en nuestro caso el truco de cambiar variables a $x \pm vt $ no sera de ayuda. Sin embargo, el análisis de Fourier es fácilmente generalizable a cualquier número de dimensiones. La idea es que, dada una función $f(x, y, z)$, puede tomar su transformada de Fourier una variable a la vez. Veamos brevemente cómo funciona esto. Para simplificar, solo consideraremos el caso de ondas en el espacio tridimensional, es decir, usaremos la versión continua de la transformada de Fourier.
La transformada de Fourier $h(\vec{k}=h(k_x,k_y,k_z)$ de $f(\vec{r})=f(x.y.z)$ esta definida como: \begin{equation} h(\vec{k})=(2\pi)^{-\frac{3}{2}} \int_{en \thinspace todo \thinspace el \thinspace espacio}d^3xe^{-i\vec{k}\cdot\vec{r}}f(\vec{r}). \end{equation}
donde $\vec{k}\cdot\vec{r}=k_xx+k_yy+k_zz$, y el factor $2\pi$ es una normalización conveniente, y cada función (integrable en cuadrado) $f(\vec{r})$ se puede expresar como: \begin{equation} f(\vec{r})=(2\pi)^{-\frac{3}{2}} \int_{en \thinspace todo \thinspace el \thinspace espacio}d^3ke^{i\vec{k}\cdotp\vec{r}}h(\vec{k}). \end{equation} y para alguna función (cuadrada integrable) $h(\vec{k})$, la región de integración en cada una de estas fórmulas se denota por "todo el espacio", lo que significa que cada uno de $(x, y, z)$ en (16) y cada uno de $k^x,k^y,k^z)$ en (17) se ejecutan desde $-\infty$ hasta $\infty$. Si $f\vec{r}$ es real, entonces su transformada de Fourier satisface: $h^*(\vec{k})=h(-\vec{k})$
Ahora tenemos que tomar en cuenta que $e^{i\vec{k}\cdotp\vec{r}}$ se puede ver como una onda plana viajando con un tiempo fijo. En esta interpretación , el plano de simetría es ortogonal a $\vec{k}$ y su longitud de onda es $\lambda= \frac{2\pi}{k}$, donde $k=\sqrt{k_x^2+k_y^2+k_z^2}$ es la magnitud del vector $\vec{k}$. Ahora debido a que $e^{i\vec{k}\cdotp\vec{r}}= e^{i\vec{k}_x\cdotp\vec{x}} e^{i\vec{k}_y\cdotp\vec{y}} e^{i\vec{k}_z\cdotp\vec{z}}$ se puede tomar la transformada de Fourier tridimensional simplemente como 3 transformadas de Fourier unidimensionales, una para cada variable espacial.
La esencia del análisis de Fourier es que cada función puede expresarse como una superposición de ondas planas con las siguientes características:
- Amplitudes variables (para $h(\vec{k})$)
- Direcciones variables (para $\frac{\vec{k}}{k}$)
- Longitudes de onda variables (para $k$)
las contribuciones de las características dependen de la función particular que está siendo analizada por Fourier. Ahora usamos este hecho básico del análisis de Fourier para tener una idea de la solución general de la ecuación de onda, esto generalizará nuestro resultado unidimensional. Suponiendo que $\psi(\vec{r},t)$ es solución a la ecuación de onda, entonces definimos:
\begin{equation} \varphi(\vec{k},t)= (2\pi)^{-\frac{3}{2}} \int_{en \thinspace todo \thinspace el \thinspace espacio}d^3 x e^{-i\vec{k}\cdotp\vec{r}}\psi(\vec{r},t). \end{equation} Esta es la transformada inversa de Fourier, por lo que la transformada de Fourier es: \begin{equation} \psi(\vec{r},t)= (2\pi)^{-\frac{3}{2}} \int_{en \thinspace todo \thinspace el \thinspace espacio}d^3 k e^{i\vec{k}\cdotp\vec{r}}\varphi(\vec{k},t). \end{equation}
Se puede ver que la ecuación de onda para $\psi$ implica que:
\[ \frac{\partial^2\varphi}{\partial t^2}=-k^2v^2\varphi, \] \begin{equation} \frac{\partial^2\varphi}{\partial t^2}+k^2v^2\varphi = 0. \end{equation}
La ecuación es igual que en el caso unidimensional, para cada valor de $k$ esto es solo la ecuación de un oscilador armónico. El vector de onda, en efecto, etiqueta los grados de libertad que oscilan con una frecuencia $w=|k|v$. Esto no casualidad, por supuesto, dada la relación entre la ecuación de onda y el oscilador armónico, la solución a (20) para cualquier $\vec{k}$ dado es de la forma:
\begin{equation} \varphi(\vec{k},t)=A(\vec{k})\cos{(wt)} + B(\vec{k})\sin{(wt)}. \end{equation}
Para obtener los coeficientes A y B es necesario considerar las condiciones iniciales. Ahora supongamos que en, $t = 0$ la posición y la velocidad de la onda se definen como:
\begin{equation} \psi(\vec{r},t=0)= \alpha(\vec{r}), \thinspace \thinspace \frac{\partial\psi(\vec{r},0)}{\partial t}=\beta(\vec{r}). \end{equation}
En donde $\alpha(\vec{r})$ y $\beta(\vec{r})$ son expansiones de Fourier dadas por:
\begin{equation} \alpha(\vec{r})= (2\pi)^{-\frac{3}{2}} \int_{en \thinspace todo \thinspace el \thinspace espacio}d^3 k e^{i\vec{k}\cdotp\vec{r}}a(\vec{k}). \end{equation}
\begin{equation} \beta(\vec{r})= (2\pi)^{-\frac{3}{2}} \int_{en \thinspace todo \thinspace el \thinspace espacio}d^3 k e^{i\vec{k}\cdotp\vec{r}}b(\vec{k}). \end{equation}
y se puede ver que
\begin{equation} A(\vec{k})=a(\vec{k}), \thinspace B(\vec{k})=\frac{1}{w}b(\vec{k}). \end{equation}
y sustituyendo en la transformada de Fourier:
\[ \psi(\vec{r},t)= (2\pi)^{-\frac{3}{2}} \int_{en \thinspace todo \thinspace el \thinspace espacio}d^3 k e^{i\vec{k}\cdotp\vec{r}}\varphi(\vec{k},t), \]
\[ \psi(\vec{r},t)= (2\pi)^{-\frac{3}{2}} \int_{en \thinspace todo \thinspace el \thinspace espacio}d^3 k e^{i\vec{k}\cdotp\vec{r}}\left(A(\vec{k})\cos{(wt)} + B(\vec{k})\sin{(wt)} \right), \]
\begin{equation}
\psi(\vec{r},t)= (2\pi)^{-\frac{3}{2}} \int_{en \thinspace todo \thinspace el \thinspace espacio}d^3 k e^{i\vec{k}\cdotp\vec{r}}\left(a(\vec{k})\cos{(wt)} + \frac{1}{w}b(\vec{k})\sin{(wt)} \right).
\end{equation}
con
\[
\alpha(\vec{r})= (2\pi)^{-\frac{3}{2}} \int_{en \thinspace todo \thinspace el \thinspace espacio}d^3 x e^{i\vec{k}\cdotp\vec{r}} \alpha(\vec{r}),
\]
\begin{equation}
\alpha(\vec{r})= (2\pi)^{-\frac{3}{2}} \int_{en \thinspace todo \thinspace el \thinspace espacio}d^3 x e^{i\vec{k}\cdotp\vec{r}} \psi(\vec{r},0).
\end{equation}
y
\[ \beta(\vec{r})= (2\pi)^{-\frac{3}{2}} \int_{en \thinspace todo \thinspace el \thinspace espacio}d^3 x e^{i\vec{k}\cdotp\vec{r}}\beta(\vec{r}), \] \begin{equation} \beta(\vec{r})= (2\pi)^{-\frac{3}{2}} \int_{en \thinspace todo \thinspace el \thinspace espacio}d^3 x e^{i\vec{k}\cdotp\vec{r}} \frac{\partial\psi(\vec{r},0)}{\partial t}. \end{equation}
esto satisface la ecuación de onda con la elección general de las condiciones iniciales (22). Lo que justifica llamar a la representación de Fourier (26) solución general de la ecuación de onda en tres dimensiones. La solución general de la ecuación de onda tridimensional (26) puede verse como una superposición de las soluciones de onda del plano elemental que estudiamos antes. Para ver esto, solo tenga en cuenta la definición de $\sin(wt)$ y $\cos(wt)$ con exponenciales complejas que podemos ver en Numeros complejos, para sustituir los términos en (26) y obtener la solución en la siguiente forma:
\begin{equation} \psi(\vec{r},t)= (2\pi)^{-\frac{3}{2}} \int_{en \thinspace todo \thinspace el \thinspace espacio \thinspace k}d^3 k \left[ c(\vec{k})e^{i(\vec{k}\cdotp\vec{r}-kvt)}+c^*(\vec{k})e^{-i(\vec{k}\cdotp\vec{r}-kvt)}\right] \end{equation} donde $c(\vec{k})$ esta definido por las condiciones iniciales.
Físicamente, se puede pensar que esta fórmula representa una superposición (continua) de ondas planas. Para ver esto, tenemos que considerar una onda plana de la forma:
\begin{equation} \psi(\vec{r},t)=Re\left[ce^{i(\vec{k}\cdotp\vec{r}-wt)}\right], \thinspace c \thinspace\epsilon \thinspace \mathbb C \end{equation}
Se puede comprobar que se trata de una onda que viaja en la dirección de $\vec{k}$, con longitud de onda $\lambda=\frac{2\pi}{k}$ y con una amplitud $| c |$. La fase $\frac{c}{|c|}$ del número complejo da una constante a la fase de la onda. La integral en (26) es entonces una superposición de ondas en las que se varían las amplitudes ($|c|$), las fases relativas $(\frac{c}{|c|})$, las longitudes de onda $\lambda=\frac{2\pi}{k}$ y las direcciones de propagación ($\frac{\vec{k}}{k}$) de una onda a la siguiente.
De manera equivalente, toda solución a la ecuación de onda se puede obtener superponiendo soluciones de onda plana real de la forma:
\begin{equation}
\psi(\vec{r},t)=A\cos(\vec{k}\cdot\vec{r}-wt+\phi)
\end{equation}
en esta ecuación la superposición se da variando la amplitud $A$, el vector de onda $\vec{k}$ y la fase $\phi$. Podemos ver el espacio de soluciones de la ecuación de onda tridimensional como un espacio vectorial. Desde este punto de vista, las ondas planas forman la base del espacio vectorial de soluciones. Por lo que la solución a la ecuación de onda en tres dimensiones es:
\[
\psi(\vec{r},t)=A\cos(\vec{k}\cdot\vec{r}\mp wt+\phi)
\]
- + si se mueve en sentido negativo de su respectivo eje
- - si se mueve en sentido positivo de su respectivo eje
Referencias
- http://galileo.phys.virginia.edu/classes/152.mf1i.spring02/Waves2D_3D.htm
- https://www.physics.purdue.edu/~jones105/phys42200_Spring2013/notes/Phys42200_Lecture20.pdf
- https://digitalcommons.usu.edu/cgi/viewcontent.cgi?article=1009&context=foundation_wave
- https://demonstrations.wolfram.com/3DWaves/
: