Diferencia entre revisiones de «Invariante de Ermakov: interpretacion fisica»
| Línea 391: | Línea 391: | ||
Primeramente cambiaremos la notación de la Ec. (\ref{eq:OAA}) | Primeramente cambiaremos la notación de la Ec. (\ref{eq:OAA}) | ||
\begin{equation}\label{eq:OAA punto} | \begin{equation}\label{eq:OAA punto dep-t} | ||
\ddot{x}+\gamma\dot{x}+\Omega^2 x=0 | \ddot{x}+\gamma\dot{x}+\Omega^2 x=0 | ||
\end{equation} | \end{equation} | ||
Revisión del 12:24 16 jun 2021
La energía de un sistema mecánico que está sujeto a una fuerza conservativa dependiente linealmente del tiempo puede ser descrita mediante la formulación de variables complementarias. Sin embargo, este formalismo también puede usarse para sistemas con amortiguamiento, en donde el intercambio entre energía potencial y energía cinética de un oscilador es evidente. Es en estos sistemas donde el invariante de Ermakov es, precisamente, el intercambio de energías.
Bajo un amortiguamiento ligero la energía cinética se transforma en energía potencial cuando el sistema se acerca al punto de equilibrio, y por otra parte la energía potencial se transforma en energía cinética cuando el sistema se aleja al punto de equilibrio. Sin embargo, tenemos el ejemplo de osciladores con un fuerte amortiguamiento, en donde el coeficiente de amortiguamiento $\gamma$ es igual al coeficiente de la fuerza restitutiva $\Omega$, la energía no fluye entre estas dos formas de energía, dado que la energía cinética es disipada en el amortiguamiento y solo una pequeña cantidad regresa en forma de energía potencial.
La presente descripción está basada en el trabajo de M. Fernández-Guasti [1]
Introducción
La descripción de un oscilador amortiguado con parámetros independientes del tiempo se puede hacer con la formulación de variables complementarias. La energía total del sistema se compone de tres partes, cinética, potencial y modulación. Esta energía total tiene una dependencia exponencial en el tiempo y se mide por el invariante de primer orden independiente del tiempo $Q_{00}$, mientras que el intercambio entre energía potencial y cinética en el oscilador se mide en términos del invariante dependiente del tiempo $q_{00}$.
La formulación de variables complementarias provee un conjunto de invariantes para ecuaciones diferenciales de segundo orden no autónomas. Estos invariantes son combinaciones bilineales de las variables complementarias o de sus derivadas, las cuales, claramente dependen del contexto del sistema mecánico.
Recordemos que las ecuaciones diferenciales autónomas de orden $k %mayor o igual que 1$ Son de la forma
\begin{equation} y^{(k)}=F(y, y^{\prime}, y^{\prime\prime},...,y^{(k-1)}). \end{equation}
Y una función $f$ se dice bilineal en un espacio vectorial $V$ sobre un campo $\mathbb{F}$, tal que, $f:V\times V \rightarrow \mathbb{F} $ si es lineal con respecto a cada uno de sus argumentos,
\begin{equation*} f(\alpha\,u+\beta\,v, w)=\alpha\,f(u,w)+\beta\,f(v,w) \end{equation*} \begin{equation*} f(u,\alpha\,v+\beta\,w)=\alpha\,f(u,v)+\beta\,f(u,w) \end{equation*}
Osciladores armónicos invariantes dependientes del tiempo
Se sabe que la ecuación de un oscilador armónico simple es una ecuación diferencial de segundo orden de la forma
\begin{equation*} \ddot{x} + \omega^2 x = 0 \end{equation*}
La cual es una ecuación diferencial autónoma. Sin embargo, cuando ya hay dependencia en el tiempo la forma del oscilador armónico es
\begin{equation}\label{eq:HOTD} \ddot{x}+\Omega^2 x= 0 \end{equation}
Donde $\Omega(t)^2$ es un parámetro dependiente del tiempo, por lo que se trata de una ecuación diferencial no autónoma. Al tratarse de una ecuación diferencial lineal en $x$, la Ec. (\ref{eq:HOTD}), admite la superposición de soluciones. Digamos que $x_1$ y $x_2$ son soluciones de dicha ecuación, entonces, el invariante de orden cero es
\begin{equation} Q_{00}=x_2\dot{x_1}-\dot{x_2}x_1 \end{equation}
Cómo vemos, $Q_{00}$ es el wronskiano de las dos soluciones y además es una función bilineal, tal como se dijo en la sección anterior.
Si expresamos a $x_1$ y $x_2$ en forma trigonométrica con $\rho$ siendo la amplitud y $\phi$ la fase, como sigue
\begin{equation*} x_1=\rho\sin\phi \end{equation*}
\begin{equation*} x_2=\rho\cos\phi \end{equation*}
entonces, el invariante $Q_{00}$ toma la siguiente forma
\begin{equation*} Q_{00}=\rho^2\phi\cos^2\phi+\rho^2\phi\sin^2\phi=\rho^2\phi. \end{equation*}
Podemos hacer un cambio de sistema coordenado, en el que ahora nuestras variables son $x_1$ o $x_2$ y $\rho$, de tal forma que el invariante $Q_{00}$ queda expresado como sigue
\begin{equation}\label{eq:invariante Q00} Q_{00}=\dfrac{\rho}{\sqrt{\rho^2-x_1}}(x_1\dot{\rho}-\rho\dot{x_1}) \end{equation}
es decir, está representado en términos de la posición y de la amplitud.
El invariante de Ermakov-Lewis usualmente se escribe como $I=\dfrac{1}{2}\left(h\dfrac{x^2}{\rho^2}+(x\dot{\rho}-\rho\dot{x})^2\right)$, que en términos de $Q_{00}$ es
\begin{equation}\label{eq:invariante de Ermakov} I=\dfrac{1}{2}Q_{00}^2 =\dfrac{1}{2}\left(Q_{00}^2\dfrac{x^2}{\rho^2}+(x\dot{\rho}+\rho\dot{x})^2\right). \end{equation}
Comprobación
Iniciamos con el lado izquierdo de la ecuación (\ref{eq:invariante de Ermakov}) \begin{equation*} Q_{00}^2\dfrac{x_1^2}{\rho^2}+(x_1\dot{\rho}-\rho\dot{x_1})^2=\dfrac{x_1^2}{\rho^2-x_1^2}(x_1\dot{\rho}-\rho\dot{x_1})^2+ (x_1\dot{\rho}-\rho\dot{x_1})^2\\ = (x_1\dot{\rho}-\rho\dot{x_1})^2\left[1+\dfrac{x_1^2}{\rho^2-x_1^2}\right]\\ = (x_1\dot{\rho}-\rho\dot{x_1})^2\left[\dfrac{\rho^2}{\rho^2-x_1^2}\right]=Q_{00}^2 \end{equation*}
Fin de la comprobación
Oscilador armónico amortiguado
La forma del oscilador armónico amortiguado es la siguiente
\begin{equation} \label{eq:OAA} \dfrac{d^2 x}{dt^2}+\gamma \dfrac{dx}{dt}+\Omega^2x=0. \end{equation}
En donde $\gamma$ es el coeficiente de amortiguamiento y $\Omega^2$ continua siendo el coeficiente de restitución, ambos coeficientes pueden ser dependientes del tiempo.
Intercambio de energía
Cómo podemos ver el coeficiente de amortiguamiento es lineal, por lo que se siguen permitiendo la superposición de soluciones. Digamos que $x_1$ y $x_2$ son soluciones de la Ec. (\ref{eq:OAA}), entonces se cumple
\begin{equation*} \dfrac{d^2x_1}{dt^2}+\gamma\dfrac{dx_1}{dt}+\Omega^2 x_1=0\\ \dfrac{d^2x_2}{dt^2}+\gamma\dfrac{dx_2}{dt}+\Omega^2 x_2=0 \end{equation*} Y dado que $x_1$ y $x_2$ son soluciones no triviales, entonces
\begin{equation*} x_2\dfrac{d^2x_1}{dt^2}+x_2\gamma\dfrac{dx_1}{dt}+x_2\Omega^2 x_1=0\\ x_1\dfrac{d^2x_2}{dt^2}+x_1\gamma\dfrac{dx_2}{dt}+x_1\Omega^2 x_2=0 \end{equation*}
Si tomamos la diferencia entre estas dos ecuaciones
\begin{equation*} x_2\dfrac{d^2x_1}{dt^2}-x_1\dfrac{d^2x_2}{dt^2}+\gamma\left[x_2\dfrac{dx_1}{dt}-x_1\dfrac{x_2}{dt}\right]=0 \end{equation*}
Cambiando de notación,
\begin{equation} \label{eq:diferencia entre soluciones} x_2\ddot{x_1}-x_1\ddot{x_2}+\gamma(x_2\dot{x_1}-x_1\dot{x_2})=0 \end{equation}
De ésta última expresión reconocemos $x_2\dot{x_1}-x_1\dot{x_2}$ como el invariante $q_{00}$ (La notación en mayúsculas - $Q_{ij}$ - está reservado para los invariantes independientes del tiempo, lo contrario a la notación en minúscula)
\begin{equation}\label{eq:def invariante q00} q_{00}=x_2\dot{x_1}-x_1\dot{x_2} \end{equation}
Ahora bien, si tomamos la derivada del invariante $q_{00}$ con respecto al tiempo obtenemos
\begin{equation*} \dfrac{dq_{00}}{dt}=\dfrac{d}{dt}(x_2\dot{x_1}-x_1\dot{x_2})\\ =\dot{x_2}\dot{x_1}+x_2\ddot{x_1}-\dot{x_1}\dot{x_2}-x_1\ddot{x_2}\\ =x_2\ddot{x_1}-x_1\ddot{x_2} \end{equation*}
que corresponde a los dos primeros términos de la Ec. (\ref{eq:diferencia entre soluciones}). Por lo tanto, podemos escribir ésta ecuación en términos del invariante $q_{00}$,
\begin{equation} \dfrac{d}{dt}q_{00}+\gamma q_{00} =0 \end{equation}
Como sabemos, la solución a esta ecuación es
\begin{equation}\label{eq:invariante q00} q_{00}(t)=Q_{00}\exp\left(-\int\gamma dt\right) \end{equation}
De aquí obtenemos las expresiones para el intercambio de energía \begin{equation*} \mathcal{E}^{ex}_\omega \equiv \dfrac{1}{2}mq_{00} \end{equation*}
Y el intercambio de energía invariante
\begin{equation*} \mathcal{I}^{ex}_\omega \equiv \dfrac{1}{2}mQ_{00}. \end{equation*}
Energía e invariante $Q_{10}$
Para esta sección usaremos la metodología y resultados de variables complementarias.
Primeramente cambiaremos la notación de la Ec. (\ref{eq:OAA})
\begin{equation}\label{eq:OAA punto} \ddot{x}+\gamma\dot{x}+\Omega^2 x=0 \end{equation}
Sabemos que $v=\dot{x}$, entonces si tomamos la derivada temporal de la Ec. (\ref{eq:OAA punto})
\begin{equation*} \ddot{v}+\gamma \dot{v}+\Omega^2 v+ \dot{\gamma} v +\dot{\Omega^2}x=0 \end{equation*}
Multiplicando esta ecuación por $x$
\begin{equation}\label{eq:variables complementarias 1} x\ddot{v}+\gamma x\dot{v}+\Omega^2 xv+ \dot{\gamma} xv +\dot{\Omega^2}x^2=0 \end{equation}
Ahora bien, el producto de la Ec. (\ref{eq:OAA punto}) con $v$ es
\begin{equation}\label{eq:variables complementarias 2} v\ddot{x}+\gamma v\dot{x}+\Omega^2 vx=0 \end{equation}
La diferencia de la Ec. (\ref{eq:variables complementarias 2}) menos la Ec. (\ref{eq:variables complementarias 1}) es
\begin{equation}\label{eq:diferencia variables complementarias} \dfrac{d}{dt}\left(v\dfrac{dx}{dt}-x\dfrac{dv}{dt}\right)+\gamma\left(v\dfrac{dx}{dt}-x\dfrac{dv}{dt}\right)-\dfrac{d\gamma}{dt}xv-\dfrac{d\Omega^2}{dt}x^2=0 \end{equation}
Notemos que el primer término de la Ec. (\ref{eq:diferencia variables complementarias}) se puede escribir en términos del w-bracket, es decir
\begin{equation*} \lfloor v, x \rfloor = v \dfrac{dx}{dt}-x\dfrac{dv}{dt}=v\dfrac{dx}{dt}-x\dfrac{dv}{dt}=v^2 +\Omega^2x^2 +\gamma x v \end{equation*}
Este w-bracket está asociado con la energía del objeto en presencia de fuerzas restitutivas y de amortiguamiento, por lo que, $q_{10}=\lfloor v, x \rfloor$.
Multiplicando la Ec. (\ref{eq:diferencia variables complementarias}) por el factor de integración $\exp\left(\int\gamma dt\right)$, obtenemos
\begin{equation*} \dfrac{d}{dt}\left[(v^2+\Omega^2x^2 +\gamma x v )\exp\left(\int\gamma dt\right)\right]- \left[\dfrac{d\gamma}{dt}xv +\dfrac{d\Omega^2}{dt}x^2\right]\exp\left(\int\gamma dt\right)=0 \end{equation*}
Por lo tanto el invariante $Q_{10}$ es
\begin{equation*} Q_{10}= (v^2+\Omega^2x^2+\gamma xv) \exp\left(\int \gamma dt\right)-\int \left(\dfrac{d\gamma}{dt}xv +\dfrac{d\Omega^2}{dt}x^2\right)\exp\left(\int\gamma dt\right)dt \end{equation*}
Ahora se puede incluir el factor $\frac{1}{2}m$ para completar la forma de la energía cinética y potencial. Como se vio en la sección anterior, la energía total del sistema la podemos escribir en términos del invariante $Q_{10}$
\begin{equation}\label{eq:energía total} \mathcal{E}=\dfrac{1}{2}mQ_{10}=\left(\dfrac{1}{2}mv^2+\dfrac{1}{2}m\Omega^2x^2+\dfrac{1}{2}m\gamma x c\right)\exp\left(\int \gamma dt\right)-\\- \dfrac{1}{2}m\int\left(\dfrac{d\gamma}{dt}xv+\dfrac{d\Omega^2}{dt}x^2\right)\exp\left(\int\gamma dt\right) \end{equation}
donde, $\mathcal{E}_k=\dfrac{1}{2}mv^2$ es la energía cinética; $\mathcal{E}_p=\dfrac{1}{2}m\Omega^2x^2$ es la energía potencial y $\mathcal{E}_{df}=-\dfrac{1}{2}m\int\left(\dfrac{d\gamma}{dt}xv+\dfrac{d\Omega^2}{dt}x^2\right)\exp\left(\int\gamma dt\right)$ es la energía disipada o transferida por las fuerzas disipativas o restitutivas . Mientras que el tercer término representa la modulación de energía disipativa
\begin{equation} \mathcal{E}_\gamma=\dfrac{1}{2}m\gamma x v. \end{equation}
Notemos que, cuando $\gamma=0$ entonces, el término disipativo se anula. Si reescribimos el termino disipativo como $\mathcal{E}=\dfrac{1}{2}x(m\gamma v)$ podemos ver que es igual a la fuerza de fricción por una distancia $x$, es decir, $\mathcal{E}=\dfrac{1}{2}x F_{fricción}$, dado que $F_{fricción}=m\gamma v $.
Por otra parte, el factor $\int \dot{\gamma}xv\exp\left(\int \gamma dt\right)dt$ puede estar asociado con la modulación disipativa. Este término es cero si $\gamma$ es constante o cero.
Finalmente, el término $\mathcal{E}_{df}=-\int\dfrac{d\Omega^2}{dt}x^2 dt $ representa la variación en el tiempo de la energía debida a la transferencia de la fuerza de restitución entre el objeto y el medio. La integración en el tiempo exhibe que los términos dinámicos del campo $\mathcal{E}_{df}$ tienen memoria de la evolución del sistema oscilador-campo .
Tomemos ahora el caso en el qué hay amortiguamiento y el coeficiente de la fuerza restitutiva es constante, por lo que la Ec. (\ref{eq:energía total}) queda sólo como
\begin{equation} \mathcal{E}=\dfrac{1}{2}m(v^2+\Omega^2x^2+\gamma x v )\exp\left(\int\gamma dt\right)-\dfrac{1}{2}m\int \dfrac{d\gamma}{dt}x v\exp\left(-\int\gamma dt\right) \end{equation}
Cómo se mencionó anteriormente el invariante $q_{10}$ puede tomarse como la energía en el objeto en presencia de fuerzas restitutivas y de amortiguamiento. De acuerdo a esto
\begin{equation}\label{eq:energía del objeto} \mathcal{E}_{obj}=\dfrac{1}{2} m q_{10}=\mathcal{E}_k+\mathcal{E}_p+\mathcal{E}_\gamma=(\mathcal{E}-\mathcal{E}_{df})\exp\left(-\int\gamma dt\right) \end{equation}
Pero sabemos que la energía de un oscilador generalmente se escribe solo como $\mathcal{E}_{oscilador}=\mathcal{E}_k+\mathcal{E}_p$. Sin embargo, podemos escribir la energía de un oscilador de acuerdo a la Ec. (\ref{eq:energía del objeto}) como sigue
\begin{equation}\label{eq:energía del oscilador} \mathcal{E}_{oscilador}=\left(\dfrac{1}{2}mQ_{10}+\dfrac{1}{2}m\int\dot{\gamma}xv\exp\left(\int\gamma dt\right) dt\right)\exp\left(-\int\gamma dt\right)-\dfrac{1}{2}m\gamma x \dot{x} \end{equation}
Esto nos ha permitido expresar la energía de un oscilador en dos formas: 1) como la suma de la energía cinética y potencial y 2) como la energía total del sistema menos la energía disipativa.
Coeficiente de amortiguamiento constante y parámetros independientes del tiempo
Empecemos con la solución compleja de la ecuación del oscilador con amortiguamiento constante,
\begin{equation}\label{eq:solución OAA compleja} \psi=\rho_0 \exp\left(-\dfrac{1}{2}\gamma t\right) \exp\left(-i\left(\sqrt{\Omega^2-\dfrac{1}{4}\gamma^2}t+\phi_0\right)\right) \end{equation}
donde $\rho=\rho_0\exp\left(-\dfrac{1}{2}\gamma t\right)$ es la variable de amplitud, y $\varphi = \sqrt{\Omega^2-\dfrac{1}{4}\gamma^2}t+\phi_0$ es la fase. Además, $\omega_d=\dot{\varphi}=\sqrt{\Omega^2-\dfrac{1}{4}\gamma^2}$.
Energía con amortiguamiento constante
Ahora bien, supongamos que los coeficientes de amortiguamiento y de la fuerza restitutiva son constantes, entonces la Ec. (\ref{eq:energía del oscilador}) puede ser escrita como
\begin{equation}\label{eq:energia oscilador} \mathcal{E}_{oscilador}=\dfrac{1}{2}mQ_{10}\exp\left(-\gamma t\right)-\dfrac{1}{2}m\gamma xv \end{equation}
Como vemos este resultado es importante porque es otra forma de obtener la expresión de la energía para un oscilador amortiguado, que de forma usual se obtiene con la suma de la energía cinética y potencial.
Con la descripción que se dará a continuación se hará la separación del decaimiento exponencial en la energía del oscilador. Primeramente tomemos las variables reales de la posición y la fase
\begin{equation}\label{eq:posición} x=\rho_0\exp\left(-\dfrac{1}{2} \gamma t\right)\cos(\omega_d t+\phi_0) \end{equation}
Y como sabemos, $\omega_d=\sqrt{\Omega^2-\dfrac{1}{4}\gamma^2}$.
Para determinar las constantes $\rho_0$ y $\phi_0$ se hacen uso de condiciones iniciales. Por ejemplo, $\psi(t=0)=x_0$ y $\dot{\psi}(t=0)=0$,
\begin{equation*} \phi_0=-\arctan\left(\dfrac{\gamma}{2\omega_d}\right), \qquad \rho_0=x_0\dfrac{\Omega}{\omega_d} \end{equation*}
Por lo que la energía potencial se puede escribir como
\begin{equation} \mathcal{E}_p=\dfrac{1}{2}m\rho_0^2\exp\left(-\gamma t\right)\Omega^2\cos^2(\omega_d t+\phi_0) \end{equation}
Y la energía cinética es
\begin{equation} \mathcal{E}_k=\dfrac{1}{2}m\rho_0^2\exp\left(-\gamma t \right)\left(\Omega^2\sin^2(\omega_d t+\phi_0 +\dfrac{1}{2}\gamma \Omega \sin(2\omega_d t+2\phi_0+\gamma_0)\right) \end{equation}
de esta expresión veamos los dos términos. El primero,
\begin{equation} \dfrac{1}{2}m\rho_0^2\exp\left(-\gamma t\right) \dfrac{1}{2}\gamma\Omega\sin(2\omega_dt+2\phi_0+\gamma_0) \end{equation}
corresponde a la energía disipada, cómo podemos ver tiene el término $\gamma$ que es la constante de amortiguamiento. Y por otra parte, el segundo término
\begin{equation} \dfrac{1}{2} m\rho_0^2\exp\left(-\gamma t\right)\Omega^2\sin^2(\omega_d t+\phi_0) \end{equation}
Que corresponde al intercambio entre la energía cinética y potencial.
Ahora bien, de la Ec. (\ref{eq:posición}) podemos tomar $\dot{x}=v$ y evaluar el w-bracket en función de $x$ y $v$, lo que resulta en
\begin{equation} \lfloor x, v \rfloor = \rho_0^2\exp\left(-\gamma t \right) \Omega \omega_d \end{equation}
Que como vimos anteriormente $q_{00}=\lfloor v,x \rfloor$ a excepción del factor constante $\Omega$. Este resultado refuerza la interpretación de que el invariante $q_{00}$ representa el intercambio dinámico entre las dos formas de energía.
Una vez que ya analizamos la energía potencial y las formas que componen a la energía cinética, veamos qué pasa con la modulación de la energía disipativa, que de acuerdo a la Ec. (\ref{eq:energia oscilador}), es
\begin{eqnarray}\label{eq:energia disipativa} \mathcal{E}_\gamma&=&\dfrac{1}{2}m\gamma x\dot{x}\\ &=&\dfrac{1}{2}m\rho_0^2\exp\left(-\gamma t\right)\left(-\dfrac{\gamma^2}{4}-\dfrac{1}{2}\gamma\Omega\sin(2\omega_d t+ 2\phi_0 +\gamma_0)\right) \end{eqnarray}
Donde $-\frac{\gamma^2}{4}$ es el corrimiento de la frecuencia y $-\frac{1}{2}\gamma\Omega\sin(2\omega_d t+2\phi_0+\gamma_0)$ es la modulación de la disipación.
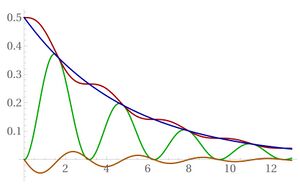
Entonces, hasta ahora se tienen las formas de la energía cinética, potencial y disipativa y como podemos ver cada una de estas tienen un decaimiento exponencial.
De la figura 1 podemos observar que el decaimiento exponencial en la modulación en la energía es necesaria porque la energía disipada tiene una dependencia en la velocidad, la cual debe ser cero cuando la energía cinética es cero. Además vemos que cuando la energía disipada se suma a la energía cinética y potencial, las oscilaciones se cancelan, lo que hace que se tenga un decaimiento suave. Dado esto, es bueno que ahora se ponga la energía disipada como parte del oscilador y no del sistema, es decir $\mathcal{E}_{oscilador}=\mathcal{E}_k+\mathcal{E}_p+\mathcal{E}_\gamma$.
Ahora bien, la energía total del sistema es
\begin{eqnarray} \nonumber\mathcal{E}&=&\exp\left(\gamma t\right)(\mathcal{E}_k+\mathcal{E}_p+\mathcal{E}_\gamma)\\ &=&\exp\left(\gamma t\right)\left(\dfrac{1}{2}m\rho_0^2\exp\left(-\gamma t\right)\Omega^2-\dfrac{1}{2}m\rho_0^2\exp\left(-\gamma t\right)\dfrac{\gamma^2}{4}\right)\\ &=&\dfrac{1}{2}m\rho_0^2\omega_d^2=\dfrac{1}{2}mQ_{10}. \end{eqnarray}
Intercambio de energía con amortiguamiento constante
De las secciones anteriores se sabe que el invariante correspondiente al intercambio de energía es $Q_{00}$, el cual se ha mencionado que es independiente del tiempo. Se puede expresar como
\begin{equation} Q_{00}=\rho_0^2\sqrt{\Omega^2-\dfrac{1}{4}\gamma^2}, \qquad \gamma \leq 2\Omega \end{equation}
Cómo vemos no tiene un decaimiento exponencial como en el caso del invariante $q_{00}$.
Esto nos sugiere, nuevamente, que los invariantes $q_{00}$ y $Q_{00}$ con una forma de medir la energía que es intercambiada periódicamente entre las dos formas de energía.
La solución linealmente independiente para $\gamma \geq 2\Omega$ es
\begin{equation*} X_{1,2}=(\rho_0)_{1,2}\exp\left[\left(-\dfrac{1}{2}\gamma\mp\sqrt{\dfrac{1}{4}\gamma^2-\Omega^2}\right)t\right] \end{equation*}
Y de la Ec. (\ref{eq:def invariante q00}) y de acuerdo a la Ec. (\ref{eq:invariante q00}), obtenemos que
\begin{equation} Q_{00}=-s\rho_{01}\rho_{02}\sqrt{\dfrac{1}{4}\gamma^2-\Omega^2},\qquad \gamma \geq 2\Omega \end{equation}
Si el invariante $Q_{00}$ es negativo o igual a cero entonces no hay intercambio de energía potencial y cinética.
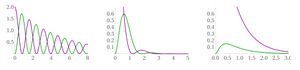
Como se mencionó al inicio de esta presentación, cuando hay un amortiguamiento fuerte la energía no fluye entre la energía cinética y potencial, dado que la energía cinética se pierde en la disipación.
Como vemos de la Figura 2 cuando $\gamma \leq \Omega$ el intercambio entre energía cinética y potencial es evidente. Cuando $\gamma=\Omega$ la energía cinética es rápidamente disipada y solamente una pequeña parte de la energía cinética se convierte en energía potencial. Finalmente, en el caso de $\gamma=3\Omega$ no se ve ningún intercambio entre energía cinética y potencial, dado que la energía potencial es convertida lentamente en energía cinética que después de disipa totalmente.
Dado esto, si no hay intercambio de energía entre las formas cinética y potencial, entonces el invariante $q_{00}$ es cero o negativo.
Energía e invariante $Q_{10}$ con parámetros dependientes del tiempo
Para esta sección usaremos la metodología y resultados de variables complementarias.
Primeramente cambiaremos la notación de la Ec. (\ref{eq:OAA})
\begin{equation}\label{eq:OAA punto dep-t} \ddot{x}+\gamma\dot{x}+\Omega^2 x=0 \end{equation}
Sabemos que $v=\dot{x}$, entonces si tomamos la derivada temporal de la Ec. (\ref{eq:OAA punto})
\begin{equation*} \ddot{v}+\gamma \dot{v}+\Omega^2 v+ \dot{\gamma} v +\dot{\Omega^2}x=0 \end{equation*}
Multiplicando esta ecuación por $x$
\begin{equation}\label{eq:variables complementarias 1} x\ddot{v}+\gamma x\dot{v}+\Omega^2 xv+ \dot{\gamma} xv +\dot{\Omega^2}x^2=0 \end{equation}
Ahora bien, el producto de la Ec. (\ref{eq:OAA punto}) con $v$ es
\begin{equation}\label{eq:variables complementarias 2} v\ddot{x}+\gamma v\dot{x}+\Omega^2 vx=0 \end{equation}
La diferencia de la Ec. (\ref{eq:variables complementarias 2}) menos la Ec. (\ref{eq:variables complementarias 1}) es
\begin{equation}\label{eq:diferencia variables complementarias} \dfrac{d}{dt}\left(v\dfrac{dx}{dt}-x\dfrac{dv}{dt}\right)+\gamma\left(v\dfrac{dx}{dt}-x\dfrac{dv}{dt}\right)-\dfrac{d\gamma}{dt}xv-\dfrac{d\Omega^2}{dt}x^2=0 \end{equation}
Notemos que el primer término de la Ec. (\ref{eq:diferencia variables complementarias}) se puede escribir en términos del w-bracket, es decir
\begin{equation*} \lfloor v, x \rfloor = v \dfrac{dx}{dt}-x\dfrac{dv}{dt}=v\dfrac{dx}{dt}-x\dfrac{dv}{dt}=v^2 +\Omega^2x^2 +\gamma x v \end{equation*}
Este w-bracket está asociado con la energía del objeto en presencia de fuerzas restitutivas y de amortiguamiento, por lo que, $q_{10}=\lfloor v, x \rfloor$.
Multiplicando la Ec. (\ref{eq:diferencia variables complementarias}) por el factor de integración $\exp\left(\int\gamma dt\right)$, obtenemos
\begin{equation*} \dfrac{d}{dt}\left[(v^2+\Omega^2x^2 +\gamma x v )\exp\left(\int\gamma dt\right)\right]- \left[\dfrac{d\gamma}{dt}xv +\dfrac{d\Omega^2}{dt}x^2\right]\exp\left(\int\gamma dt\right)=0 \end{equation*}
Por lo tanto el invariante $Q_{10}$ es
\begin{equation*} Q_{10}= (v^2+\Omega^2x^2+\gamma xv) \exp\left(\int \gamma dt\right)-\int \left(\dfrac{d\gamma}{dt}xv +\dfrac{d\Omega^2}{dt}x^2\right)\exp\left(\int\gamma dt\right)dt \end{equation*}
Ahora se puede incluir el factor $\frac{1}{2}m$ para completar la forma de la energía cinética y potencial. Como se vio en la sección anterior, la energía total del sistema la podemos escribir en términos del invariante $Q_{10}$
\begin{equation}\label{eq:energía total} \mathcal{E}=\dfrac{1}{2}mQ_{10}=\left(\dfrac{1}{2}mv^2+\dfrac{1}{2}m\Omega^2x^2+\dfrac{1}{2}m\gamma x c\right)\exp\left(\int \gamma dt\right)-\\- \dfrac{1}{2}m\int\left(\dfrac{d\gamma}{dt}xv+\dfrac{d\Omega^2}{dt}x^2\right)\exp\left(\int\gamma dt\right) \end{equation}
donde, $\mathcal{E}_k=\dfrac{1}{2}mv^2$ es la energía cinética; $\mathcal{E}_p=\dfrac{1}{2}m\Omega^2x^2$ es la energía potencial y $\mathcal{E}_{df}=-\dfrac{1}{2}m\int\left(\dfrac{d\gamma}{dt}xv+\dfrac{d\Omega^2}{dt}x^2\right)\exp\left(\int\gamma dt\right)$ es la energía disipada o transferida por las fuerzas disipativas o restitutivas . Mientras que el tercer término representa la modulación de energía disipativa
\begin{equation} \mathcal{E}_\gamma=\dfrac{1}{2}m\gamma x v. \end{equation}
Notemos que, cuando $\gamma=0$ entonces, el término disipativo se anula. Si reescribimos el termino disipativo como $\mathcal{E}=\dfrac{1}{2}x(m\gamma v)$ podemos ver que es igual a la fuerza de fricción por una distancia $x$, es decir, $\mathcal{E}=\dfrac{1}{2}x F_{fricción}$, dado que $F_{fricción}=m\gamma v $.
Por otra parte, el factor $\int \dot{\gamma}xv\exp\left(\int \gamma dt\right)dt$ puede estar asociado con la modulación disipativa. Este término es cero si $\gamma$ es constante o cero.
Finalmente, el término $\mathcal{E}_{df}=-\int\dfrac{d\Omega^2}{dt}x^2 dt $ representa la variación en el tiempo de la energía debida a la transferencia de la fuerza de restitución entre el objeto y el medio. La integración en el tiempo exhibe que los términos dinámicos del campo $\mathcal{E}_{df}$ tienen memoria de la evolución del sistema oscilador-campo .
Tomemos ahora el caso en el qué hay amortiguamiento y el coeficiente de la fuerza restitutiva es constante, por lo que la Ec. (\ref{eq:energía total}) queda sólo como
\begin{equation} \mathcal{E}=\dfrac{1}{2}m(v^2+\Omega^2x^2+\gamma x v )\exp\left(\int\gamma dt\right)-\dfrac{1}{2}m\int \dfrac{d\gamma}{dt}x v\exp\left(-\int\gamma dt\right) \end{equation}
Cómo se mencionó anteriormente el invariante $q_{10}$ puede tomarse como la energía en el objeto en presencia de fuerzas restitutivas y de amortiguamiento. De acuerdo a esto
\begin{equation}\label{eq:energía del objeto} \mathcal{E}_{obj}=\dfrac{1}{2} m q_{10}=\mathcal{E}_k+\mathcal{E}_p+\mathcal{E}_\gamma=(\mathcal{E}-\mathcal{E}_{df})\exp\left(-\int\gamma dt\right) \end{equation}
Pero sabemos que la energía de un oscilador generalmente se escribe solo como $\mathcal{E}_{oscilador}=\mathcal{E}_k+\mathcal{E}_p$. Sin embargo, podemos escribir la energía de un oscilador de acuerdo a la Ec. (\ref{eq:energía del objeto}) como sigue
\begin{equation}\label{eq:energía del oscilador} \mathcal{E}_{oscilador}=\left(\dfrac{1}{2}mQ_{10}+\dfrac{1}{2}m\int\dot{\gamma}xv\exp\left(\int\gamma dt\right) dt\right)\exp\left(-\int\gamma dt\right)-\dfrac{1}{2}m\gamma x \dot{x} \end{equation}
Esto nos ha permitido expresar la energía de un oscilador en dos formas: 1) como la suma de la energía cinética y potencial y 2) como la energía total del sistema menos la energía disipativa.
Referencias
- ↑ Fernández. G. M., Energy and energy exchange in the dissipative time dependent harmonic oscillator