Diferencia entre revisiones de «Indeterminacion»
| Línea 2: | Línea 2: | ||
describir que si es .... La amplitud es una medida del recorrido máximo de una vibbración u oscilación desde su punto de equilibrio, también es una característica que describe la intencidad de la vibración, esta tiene la carcterística de ser constante y reprersentada por la letra A. | describir que si es .... La amplitud es una medida del recorrido máximo de una vibbración u oscilación desde su punto de equilibrio, también es una característica que describe la intencidad de la vibración, esta tiene la carcterística de ser constante y reprersentada por la letra A. | ||
===Sistemas de Ermakov=== | |||
La posición de un cuerpo en un sistema mecánico discreto a menudo | |||
se expresa en términos de la amplitud y variables de fase en movimiento | |||
periódico o cuasiperiódico. Las relaciones que gobiernan las variables | |||
de posición y amplitud en una dimensión producen un par de ecuaciones | |||
de Ermakov estas ecuaciones conducen a invariantes exactos incluso | |||
en el caso donde la energía del sistema no se conserva. Los invariantes | |||
exactos son constantes de movimiento para parámetros arbitrarios dependientes | |||
del tiempo, La representación de la amplitud y la fase es concomitante | |||
a la derivación de invariantes exactas, es decir aparecen o actúan | |||
conjuntamente. Por esta razón, la determinación de estas cantidades | |||
es crucial para establecer el valor propio de los invariantes. De | |||
ahí la relevancia de los sistemas de Ermakov ya que son usados en | |||
una amplia variedad de modelos y disciplinas de física. Los sistemas | |||
de Ermakov involucran ciertos tipos de ecuaciones diferenciales ordinarias | |||
y han sido estudiados ampliamente desde finales de la década de los | |||
1970s por sus conexiones con problemas importantes de la físico-matématica, | |||
como por ejemplo, el oscilador armónico dependiente del tiempo, tanto | |||
en el caso clásico como en el cuántico. Asimismo, varios casos de | |||
la ecuación de Schrödinger, se pueden estudiar desde la óptica de | |||
estos sistemas. Por ello hablaremos un poco acerca de que son los | |||
sistemas de Ermakov En 1880, el matemático ucraniano Vasily P. Ermakov, | |||
en un artículo publicado por la Universidad de Kiev (Ucrania) presento | |||
un método para integrar ecuaciones del tipo: | |||
\begin{equation} | |||
\frac{d^{2}y}{dx}+A(x)\frac{dy}{dx}+B(x)y=0 | |||
\end{equation} | |||
Suponiendo que se conoce una solución particular de esta ecuación | |||
diferencial. Como sabemos, las ecuaciones diferenciales ordinarias | |||
lineales de segundo orden con coecientes variables, como (1), son | |||
completamente integrables solo en unos cuantos casos. Es decir no | |||
existe un método general para obtener las soluciones de este tipo | |||
de ecuaciones, a diferencia, por ejemplo, del caso de una ecuación | |||
con coeficientes constantes: | |||
\begin{equation} | |||
\frac{d^{2}y}{dx}+a\frac{dy}{dx}+by=0 | |||
\end{equation} | |||
Cuya la solución general es de la forma: | |||
\begin{equation} | |||
\varphi(x)=c_{1}\varphi_{1}(x)+c_{2}\varphi_{2}(x) | |||
\end{equation} | |||
donde $\varphi_{1}$y $\varphi_{2}$son soluciones independientes | |||
de (2) con $c_{1}$y $c_{2}$ciertas constantes. | |||
Ermakov obtiene soluciones completas para ecuaciones dela forma (1) | |||
por medio de cambios de variables que las reducen a una cuadratura | |||
(calcular una integral) también se muestra, como algunos tipos de | |||
ecuaciones no-lineales de segundo orden se pueden reducir, mediante | |||
cambios de variables apropiados, al estudio de ecuaciones del tipo | |||
(1) Uno de los ejemplos más notables que presenta Ermakov es una ecuación, | |||
que mucho tiempo después, y de manera independiente, estudiaron W. | |||
E. Milne (1930) y E. Pinney (1950), la cual representa un modelo para | |||
un oscilador armónico, dependiente del tiempo, con un potencial cuadrado | |||
inverso y que se puede escribir como : | |||
\begin{equation} | |||
\ddot{y}+\omega^{2}(t)y=\frac{1}{y^{3}} | |||
\end{equation} | |||
Donde k es una constante distinta de cero. Aquí, la notación $\dot{x},$$\ddot{x}$, | |||
... , indica las derivadas de la función $x=x(t)$ con respecto al | |||
parámetro$t$, usualmente identificado como el tiempo. La ecuación | |||
(4), es conocida como la ecuación de Ermakov-Milne-Pinney Ermakov | |||
y demuestra que la ecuación no-lineal (4) está estrechamente relacionada | |||
con el oscilador armónico dependiente del tiempo en la frecuencia: | |||
\begin{equation} | |||
\ddot{x}+\omega^{2}(t)x=0 | |||
\end{equation} | |||
La cual es una ecuacion diferencial lineal de segundo orden. Mas aun, | |||
Ermakov demostro que la funcion | |||
\begin{equation} | |||
I=\frac{1}{2}\left[(x\dot{y}-y\dot{x})^{2}+\left(\frac{x}{y}\right)^{2}\right]=C | |||
\end{equation} | |||
donde $C$ es una constante, es una integral primera de (4), lo cual | |||
se comprueba por medio de un calculo directo:$\frac{dI}{dt}=0.$Además, | |||
si $x_{1}=x_{1}(t)$ y $x_{2}=x_{2}(t)$ son son dos soluciones particulares | |||
de (5), entonces sustituyendo estas soluciones en (6) se obtienen | |||
dos soluciones para (4) A la cantidad conservada I dada por (6) se | |||
le llama invariante de Ermakov-Lewis ya que también fue encontrado | |||
posteriormente por R. Lewis en 1967, de forma independiente. Precisamente, | |||
las ecuaciones (4) y (5), junto con la integral primera (6), es lo | |||
que caracteriza a un sistema de Ermakov. Es decir, un sistema de Ermakov | |||
viene dado por dos ecuaciones acopladas ligadas por un invariante | |||
que nos permite encontrar soluciones de una ecuación, conociendo las | |||
soluciones de la otra. | |||
SISTEMAS DE ERMAKOV: | |||
\begin{thebibliography}{1} | |||
\bibitem{key-1}https://sahuarus.mat.uson.mx/index.php/sahuarus/article/download/76/63/ | |||
=== ¿Qué no es? === | === ¿Qué no es? === | ||
Revisión del 19:32 17 jun 2020
Indeterminación en la amplitud y la fase
describir que si es .... La amplitud es una medida del recorrido máximo de una vibbración u oscilación desde su punto de equilibrio, también es una característica que describe la intencidad de la vibración, esta tiene la carcterística de ser constante y reprersentada por la letra A.
Sistemas de Ermakov
La posición de un cuerpo en un sistema mecánico discreto a menudo se expresa en términos de la amplitud y variables de fase en movimiento periódico o cuasiperiódico. Las relaciones que gobiernan las variables de posición y amplitud en una dimensión producen un par de ecuaciones de Ermakov estas ecuaciones conducen a invariantes exactos incluso en el caso donde la energía del sistema no se conserva. Los invariantes exactos son constantes de movimiento para parámetros arbitrarios dependientes del tiempo, La representación de la amplitud y la fase es concomitante a la derivación de invariantes exactas, es decir aparecen o actúan conjuntamente. Por esta razón, la determinación de estas cantidades es crucial para establecer el valor propio de los invariantes. De ahí la relevancia de los sistemas de Ermakov ya que son usados en una amplia variedad de modelos y disciplinas de física. Los sistemas de Ermakov involucran ciertos tipos de ecuaciones diferenciales ordinarias y han sido estudiados ampliamente desde finales de la década de los 1970s por sus conexiones con problemas importantes de la físico-matématica, como por ejemplo, el oscilador armónico dependiente del tiempo, tanto en el caso clásico como en el cuántico. Asimismo, varios casos de la ecuación de Schrödinger, se pueden estudiar desde la óptica de estos sistemas. Por ello hablaremos un poco acerca de que son los sistemas de Ermakov En 1880, el matemático ucraniano Vasily P. Ermakov, en un artículo publicado por la Universidad de Kiev (Ucrania) presento un método para integrar ecuaciones del tipo:
\begin{equation} \frac{d^{2}y}{dx}+A(x)\frac{dy}{dx}+B(x)y=0 \end{equation}
Suponiendo que se conoce una solución particular de esta ecuación diferencial. Como sabemos, las ecuaciones diferenciales ordinarias lineales de segundo orden con coecientes variables, como (1), son completamente integrables solo en unos cuantos casos. Es decir no existe un método general para obtener las soluciones de este tipo de ecuaciones, a diferencia, por ejemplo, del caso de una ecuación con coeficientes constantes:
\begin{equation} \frac{d^{2}y}{dx}+a\frac{dy}{dx}+by=0 \end{equation}
Cuya la solución general es de la forma:
\begin{equation} \varphi(x)=c_{1}\varphi_{1}(x)+c_{2}\varphi_{2}(x) \end{equation}
donde $\varphi_{1}$y $\varphi_{2}$son soluciones independientes de (2) con $c_{1}$y $c_{2}$ciertas constantes.
Ermakov obtiene soluciones completas para ecuaciones dela forma (1) por medio de cambios de variables que las reducen a una cuadratura (calcular una integral) también se muestra, como algunos tipos de ecuaciones no-lineales de segundo orden se pueden reducir, mediante cambios de variables apropiados, al estudio de ecuaciones del tipo (1) Uno de los ejemplos más notables que presenta Ermakov es una ecuación, que mucho tiempo después, y de manera independiente, estudiaron W. E. Milne (1930) y E. Pinney (1950), la cual representa un modelo para un oscilador armónico, dependiente del tiempo, con un potencial cuadrado inverso y que se puede escribir como :
\begin{equation} \ddot{y}+\omega^{2}(t)y=\frac{1}{y^{3}} \end{equation}
Donde k es una constante distinta de cero. Aquí, la notación $\dot{x},$$\ddot{x}$, ... , indica las derivadas de la función $x=x(t)$ con respecto al parámetro$t$, usualmente identificado como el tiempo. La ecuación (4), es conocida como la ecuación de Ermakov-Milne-Pinney Ermakov y demuestra que la ecuación no-lineal (4) está estrechamente relacionada con el oscilador armónico dependiente del tiempo en la frecuencia:
\begin{equation} \ddot{x}+\omega^{2}(t)x=0 \end{equation}
La cual es una ecuacion diferencial lineal de segundo orden. Mas aun, Ermakov demostro que la funcion
\begin{equation} I=\frac{1}{2}\left[(x\dot{y}-y\dot{x})^{2}+\left(\frac{x}{y}\right)^{2}\right]=C \end{equation}
donde $C$ es una constante, es una integral primera de (4), lo cual se comprueba por medio de un calculo directo:$\frac{dI}{dt}=0.$Además, si $x_{1}=x_{1}(t)$ y $x_{2}=x_{2}(t)$ son son dos soluciones particulares de (5), entonces sustituyendo estas soluciones en (6) se obtienen dos soluciones para (4) A la cantidad conservada I dada por (6) se le llama invariante de Ermakov-Lewis ya que también fue encontrado posteriormente por R. Lewis en 1967, de forma independiente. Precisamente, las ecuaciones (4) y (5), junto con la integral primera (6), es lo que caracteriza a un sistema de Ermakov. Es decir, un sistema de Ermakov viene dado por dos ecuaciones acopladas ligadas por un invariante que nos permite encontrar soluciones de una ecuación, conociendo las soluciones de la otra.
SISTEMAS DE ERMAKOV: \begin{thebibliography}{1} \bibitem{key-1}https://sahuarus.mat.uson.mx/index.php/sahuarus/article/download/76/63/
¿Qué no es?
Veremos que no es, por ejemplo entonces esto es asi
Mfgwi (discusión) 16:41 21 may 2020 (CDT)
No es la incertidumbre cuántica
No es la indeterminación de transformadas de Fourier
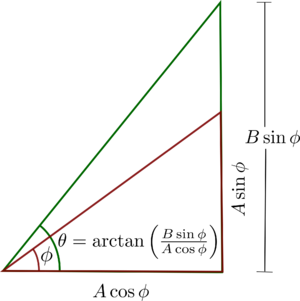
representación de amplitud y fase
Mfgwi (discusión) 20:19 16 may 2020 (CDT)
pensé que esta imagen les podría ser útil ...
indeterminación [1]
- ↑ M. Fernández-Guasti. Indeterminacy of amplitude and phase variables in classical dynamical systems: the harmonic oscillator. Europhysics Letters, 74(6):1013-1019, 2006 https://luz.izt.uam.mx/mfg/arti/06-10/ampind-epl06.pdf