Diferencia entre revisiones de «Holografía»
| Línea 10: | Línea 10: | ||
==Recostrucción del frente de onda== | ==Recostrucción del frente de onda== | ||
La reconstrucción de un frente de onda se divide en dos etapas: | |||
*Una etapa de detección | *Una etapa de detección | ||
*Una etapa de reconstrucción | *Una etapa de reconstrucción | ||
===Etapa de detección=== | ===Etapa de detección=== | ||
En esta etapa | En esta etapa se detecta la información codificada en la amplitud y la fase de las ondas. Dado que los medios de grabación solamente pueden registrar la intensidad de la luz (debido a que la información de fase de la onda colapsa), la fase se reconstruye midiendo las variaciones de intensidad en el campo a reconstruir con respecto a una onda de referencia, a esta técnica se les conoce como interferometría. En esencia, la interferometría consiste en hacer interactuar el frente de onda que resulta de la difracción de la luz por el objeto de interés y un segundo frente de onda que desempeña el papel de onda de referencia, el cual es coherente al primero y cuya amplitud y fase son bien conocidas | ||
Entonces si el frente de onda que se detecta y que se quiere reconstruir esta dado por | Entonces si el frente de onda que se detecta y que se quiere reconstruir esta dado por | ||
| Línea 29: | Línea 29: | ||
Mientras que las dos primeras formas de esta expresión dependen de las intensidades de las ondas individuales, la tercera depende de sus fases relativas <ref>[Introduction to Fourier Optics,W. Goodman Joseph, Third Edition, pag. 299]</ref> | Mientras que las dos primeras formas de esta expresión dependen de las intensidades de las ondas individuales, la tercera depende de sus fases relativas <ref>[Introduction to Fourier Optics,W. Goodman Joseph, Third Edition, pag. 299]</ref> | ||
Durante la etapa de detección | Durante la etapa de detección, tanto la detección de la luz como la modulación del frente de onda se realizan mediante una película o placa fotográfica a lo que se le conoce como $Holograma$ y matemáticamente corresponde a la función $I$. | ||
Para construir la onda de referencia se necesitan una serie de condiciones iniciales, para realizar algunos ejemplos usamos las siguientes | Para construir la onda de referencia se necesitan una serie de condiciones iniciales, para realizar algunos ejemplos usamos las siguientes | ||
| Línea 45: | Línea 45: | ||
*Holograma a partir de un objeto circular | *Holograma a partir de un objeto circular | ||
Tenemos un objeto circular que nos describirá el frente de onda que se quiere detectar y | Tenemos un objeto circular que nos describirá el frente de onda que se quiere detectar y reconstruir, este frente de onda se puede describir con la función $circ(r)$, entonces | ||
:<math> \Psi(x,y)=circ(r_c/R_c) </math> | :<math> \Psi(x,y)=circ(r_c/R_c) </math> | ||
donde $r_c=\sqrt{x^2+y^2}$, $R_c$ el radio de mi objeto y | donde $r_c$ es la ecuación de la circunferencia ($r_c=\sqrt{x^2+y^2}$), $R_c$ el radio de mi objeto y la funcion $circ(r_c)$ se escribe como | ||
\[circ(r_c)=\left\{ \begin{array}{rcl} | \[circ(r_c)=\left\{ \begin{array}{rcl} | ||
1 & \mbox{si} & r_c\leq 1\\ | 1 & \mbox{si} & r_c\leq 1\\ | ||
| Línea 60: | Línea 60: | ||
*Holograma a partir de un objeto cuadrado | *Holograma a partir de un objeto cuadrado | ||
Ahora el frente de onda que se quiere detectar lo | Ahora el frente de onda que se quiere detectar lo describirá un objeto cuadrado. La función asociada $\Psi(x,y)$ es | ||
:<math>\Psi(x,y)=rect(ax)rect(by)</math> | :<math>\Psi(x,y)=rect(ax)rect(by)</math> | ||
donde $ax$ y $ay$ son las medidas de los lados y la funcion $rect(x)$ esta dada por | donde $ax$ y $ay$ son las medidas de los lados y la funcion $rect(x)$ esta dada por | ||
| Línea 70: | Línea 70: | ||
\right. \] | \right. \] | ||
(En este | (En este caso se usó un cuadrado de $ax=by=5x10^{-4}cm$ de lado) | ||
Por tanto el holograma $I$ para el objeto cuadrado es | Por tanto el holograma $I$ para el objeto cuadrado es | ||
[[Archivo:Cuadrado Holografia.jpg|miniaturadeimagen|izquierda|Objeto cuadrado]] | [[Archivo:Cuadrado Holografia.jpg|miniaturadeimagen|izquierda|Objeto cuadrado]] | ||
| Línea 84: | Línea 84: | ||
:<math> \Psi(x,y)=\Psi_1(x,y)-\Psi_2(x,y)=disk(r_c/r_e)-disk(r_c/r_i)</math> | :<math> \Psi(x,y)=\Psi_1(x,y)-\Psi_2(x,y)=disk(r_c/r_e)-disk(r_c/r_i)</math> | ||
donde $r_c=\sqrt{x^2+y^2}$ | donde de igual manera que la circulo, se usó la ecuación de la circunferencia descrita por $r_c=\sqrt{x^2+y^2}$ pero ahora usando dos radios que son $r_i$ el radio interior, $r_e$ el radio exterior y la función $disk(r_c)$ se escribe como | ||
\[disk(r_c)=\left\{ \begin{array}{rcl} | \[disk(r_c)=\left\{ \begin{array}{rcl} | ||
0 & \mbox{si} & x\leq 1\\ | 0 & \mbox{si} & x\leq 1\\ | ||
| Línea 91: | Línea 91: | ||
\end{array} | \end{array} | ||
\right. \] | \right. \] | ||
(en este caso | (en este caso se utilizó un radio interior de $r_i=3x10^{-4}cm$ y un radio exterior de $r_e=5x10^{-4}cm$) entonces la construcción del holograma $I$ es | ||
[[Archivo:Anillo Holografia.jpg|miniaturadeimagen|izquierda|Objeto en forma de anillo]] | [[Archivo:Anillo Holografia.jpg|miniaturadeimagen|izquierda|Objeto en forma de anillo]] | ||
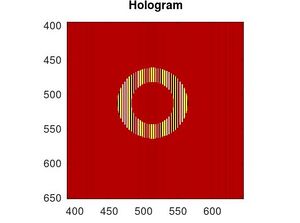
[[Archivo:Holograma Anillo.jpg|miniaturadeimagen|centro|Construccion del holograma]] | [[Archivo:Holograma Anillo.jpg|miniaturadeimagen|centro|Construccion del holograma]] | ||
===Etapa de reconstrucción=== | ===Etapa de reconstrucción=== | ||
La etapa de reconstrucción incluye varios procesos e incorpora la aplicación de la ''Transformada de Fourier''. A partir de esta transformación, el holograma se describe en el espacio de frecuencias, con el fin de calcular el campo final y reconstruir el frente de onda de interés. Consideremos que el campo final se escribe como | |||
Consideremos que el campo final se escribe como | |||
:<math> \Psi_f=\mathcal{F}\{I\} </math> | :<math> \Psi_f=\mathcal{F}\{I\} </math> | ||
Si desarrollamos tenemos que | Si desarrollamos tenemos que | ||
Revisión del 15:09 10 jun 2021
--Alma (discusión) 00:47 2 jun 2021 (CDT)
Historia
La holografía fue propuesta por Dennis Gabor en 1948, esta idea consiste en obtener imágenes en solo dos etapas, sin la necesidad de utilizar lentes ópticos. Gabor denomino a esta técnica reconstrucción del frente de onda
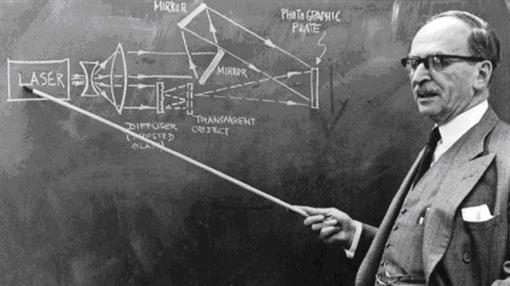
"Gabor reconoció que cuando una onda de referencia coherente adecuada está presente simultáneamente con la luz difractada o dispersada por un objeto, entonces la información sobre la amplitud y la fase de las ondas difractadas o dispersadas puede ser registrada, a pesar del hecho de que los medios de grabación responden sólo a la intensidad de la luz."[2] Gabor acuño el termino de Holograma al patrón de interferencia registrado, a partir del cual se puede obtener una imagen del objeto original.
En 1971, Gabor recibió el premio Nobel de Física por su invento.
Recostrucción del frente de onda
La reconstrucción de un frente de onda se divide en dos etapas:
- Una etapa de detección
- Una etapa de reconstrucción
Etapa de detección
En esta etapa se detecta la información codificada en la amplitud y la fase de las ondas. Dado que los medios de grabación solamente pueden registrar la intensidad de la luz (debido a que la información de fase de la onda colapsa), la fase se reconstruye midiendo las variaciones de intensidad en el campo a reconstruir con respecto a una onda de referencia, a esta técnica se les conoce como interferometría. En esencia, la interferometría consiste en hacer interactuar el frente de onda que resulta de la difracción de la luz por el objeto de interés y un segundo frente de onda que desempeña el papel de onda de referencia, el cual es coherente al primero y cuya amplitud y fase son bien conocidas
Entonces si el frente de onda que se detecta y que se quiere reconstruir esta dado por
y la onda de referencia con la que interfiere $R(x,y)$ esta descrita como:
en donde $|\Psi(x,y)|$ y $|R(x,y)|$ son las normas de las funciones $\Psi(x,y)$ y $R(x,y)$ respectivamente, entonces definimos el cuadrado de la suma de las ondas como la intensidad de propagación:
Desarrollando tenemos que
Mientras que las dos primeras formas de esta expresión dependen de las intensidades de las ondas individuales, la tercera depende de sus fases relativas [3]
Durante la etapa de detección, tanto la detección de la luz como la modulación del frente de onda se realizan mediante una película o placa fotográfica a lo que se le conoce como $Holograma$ y matemáticamente corresponde a la función $I$.
Para construir la onda de referencia se necesitan una serie de condiciones iniciales, para realizar algunos ejemplos usamos las siguientes
- $x_0$: La distancia del objeto a donde se construirá el holograma (En este caso $x_0=2 cm$)
- $f$: La distancia del holograma a donde se vera la reconstrucción del campo (Para este ejemplo es $f=0.2 cm$)
- $\lambda$: Longitud de onda de la onda de referencia (En este caso $\lambda=500x10^{-9}$)
- $f_0$: Distancia focal de la onda y esta dada por $x_0/\lambda f$
- $k$: El numero de onda que se describe como $2\pi/\lambda$
- $X$: Longitud a donde termina la onda
Entonces la onda de referencia, con estas condiciones tenemos que $r(x,y)=-2\pi f_0X$ por tanto
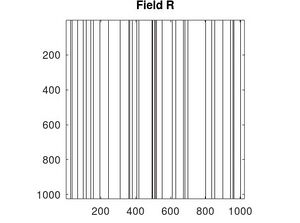
A continuación se muestra la onda de referencia (onda plana)
A continuación vamos a observar los hologramas obtenidos a partir de distintos objetos con forma regular.
- Holograma a partir de un objeto circular
Tenemos un objeto circular que nos describirá el frente de onda que se quiere detectar y reconstruir, este frente de onda se puede describir con la función $circ(r)$, entonces
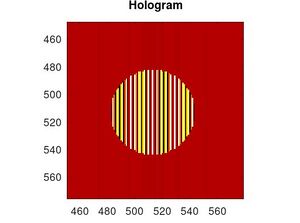
donde $r_c$ es la ecuación de la circunferencia ($r_c=\sqrt{x^2+y^2}$), $R_c$ el radio de mi objeto y la funcion $circ(r_c)$ se escribe como \[circ(r_c)=\left\{ \begin{array}{rcl} 1 & \mbox{si} & r_c\leq 1\\ & & \\ 0 & \mbox{si} & r_c\geq 1 \\ \end{array} \right. \] (Para este ejemplo quise usar un radio de $R_c=3x10^{-4} cm$ para el objeto circular). Entonces la construcción del holograma $I$ del objeto circular es
- Holograma a partir de un objeto cuadrado
Ahora el frente de onda que se quiere detectar lo describirá un objeto cuadrado. La función asociada $\Psi(x,y)$ es
donde $ax$ y $ay$ son las medidas de los lados y la funcion $rect(x)$ esta dada por \[rect(x)=\left\{ \begin{array}{rcl} 1 & \mbox{si} & x\leq 0.5\\ & & \\ 0 & \mbox{si} & x\geq 0.5\\ \end{array} \right. \]
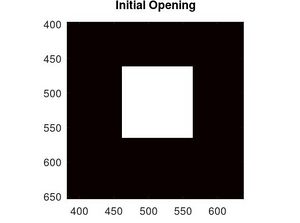
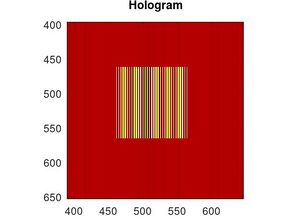
(En este caso se usó un cuadrado de $ax=by=5x10^{-4}cm$ de lado) Por tanto el holograma $I$ para el objeto cuadrado es
- Holograma a partir de un objeto en forma de un anillo
Tenemos ahora un frente de onda para detectar que el objeto que la describe es un anillo, la funciones que se utilizaron fueron
Por tanto podemos escribir el frente de onda total como
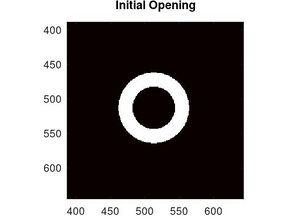
donde de igual manera que la circulo, se usó la ecuación de la circunferencia descrita por $r_c=\sqrt{x^2+y^2}$ pero ahora usando dos radios que son $r_i$ el radio interior, $r_e$ el radio exterior y la función $disk(r_c)$ se escribe como \[disk(r_c)=\left\{ \begin{array}{rcl} 0 & \mbox{si} & x\leq 1\\ & & \\ 0.5 & \mbox{si} & x=1\\ \end{array} \right. \] (en este caso se utilizó un radio interior de $r_i=3x10^{-4}cm$ y un radio exterior de $r_e=5x10^{-4}cm$) entonces la construcción del holograma $I$ es
Etapa de reconstrucción
La etapa de reconstrucción incluye varios procesos e incorpora la aplicación de la Transformada de Fourier. A partir de esta transformación, el holograma se describe en el espacio de frecuencias, con el fin de calcular el campo final y reconstruir el frente de onda de interés. Consideremos que el campo final se escribe como
Si desarrollamos tenemos que
De aqui podemos llamar a $I_{\Sigma}(x,y)=|R(x,y)|^2+|\Psi(x,y)|^2$ entonces
Pero por la propiedad de entonces
Para no escribir todo esto podemos definir que
- $\mathcal{F}\{I_{\Sigma}(x,y)\}=\widetilde{I}_{\Sigma}(f_x,f_y)$
- $\mathcal{F}\{R(x,y)\}=\widetilde{R}(f_x,f_y)$
- $\mathcal{F}\{\overline{R}(x,y)\}=\widetilde{\overline{R}}(f_x,f_y)$
- $\mathcal{F}\{\Psi(x,y)\}=\widetilde{\Psi}(f_x,f_y)$
- $\mathcal{F}\{\overline{\Psi}(x,y)\}=\widetilde{\overline{\Psi}}(f_x,f_y)$
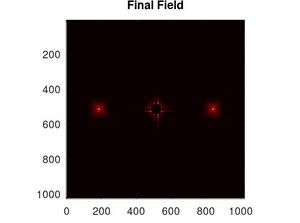
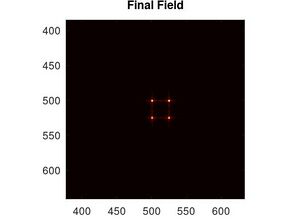
entonces podemos escribir el campo final como
Este ultimo resultado describe graficamente para cada uno de nuestros ejemplos anteriores lo siguiente:
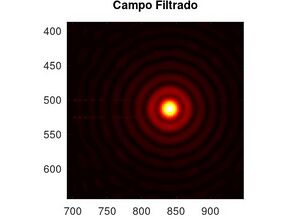
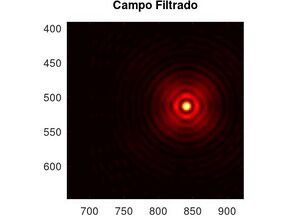
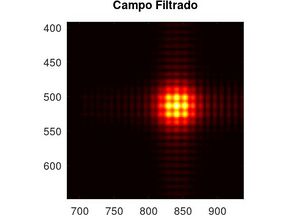
A este resultado, si le colocamos un filtro oscuro que lo podemos denominar una funcion $G(f_x,f_y)$ que predomina en el espacio de frecuencias para que el campo final filtrado sea:
Con este se tiene el campo final de cada objeto filtrado:
Por ultimo solo aplicamos transformada de Fourier al campo final filtrado $\Psi_{f-filtrado}$
Sea $I_{Reconstruido}=\mathcal{F}\{\Psi_{f-filtrado}\}$ entonces
Por las propiedades de y entonces
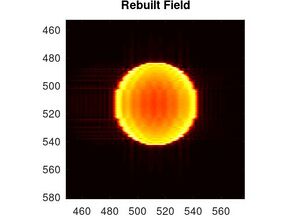
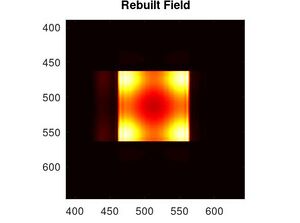
Por tanto todo este resultado nos da como solución la reconstrucción del frente de onda, aquí se muestran la reconstrucción de cada uno de los objetos que se trabajaron
Referencias
- ↑ https://static3.abc.es/media/tecnologia/2017/08/11/holografia-k4WE--510x286@abc.jpg
- ↑ Introduction to Fourier Optics,W. Goodman Joseph, Third Edition, pag. 297
- ↑ [Introduction to Fourier Optics,W. Goodman Joseph, Third Edition, pag. 299]


![{\displaystyle I=[\Psi (x,y)+R(x,y)]^{2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d141de60a52a54f87a69f4f687730db7a893a77d)
![{\displaystyle I=[\Psi (x,y)+R(x,y)][{\overline {\Psi }}(x,y)+{\overline {R}}(x,y)]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/51f5e9f2e863b8045e39975fb6a6ffe375ae9375)














![{\displaystyle \Psi _{f-filtrado}=\Psi _{f}\cdot G(f_{x},f_{y})={\widetilde {I}}_{\Sigma }(f_{x},f_{y})\cdot G(f_{x},f_{y})+[{\widetilde {R}}(f_{x},f_{y})\otimes {\widetilde {\overline {\Psi }}}(f_{x},f_{y})]G(f_{x},f_{y})+[{\widetilde {\overline {R}}}(f_{x},f_{y})\otimes {\widetilde {\Psi }}(f_{x},f_{y})]G(f_{x},f_{y})}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/501a5eea1cc8ea2de7b12626e3185fb4968ca8ea)

![{\displaystyle I_{Reconstruido}={\mathcal {F}}\{{\widetilde {I}}_{\Sigma }(f_{x},f_{y})\cdot G(f_{x},f_{y})\}+{\mathcal {F}}\{[{\widetilde {R}}(f_{x},f_{y})\otimes {\widetilde {\overline {\Psi }}}(f_{x},f_{y})]G(f_{x},f_{y})\}+{\mathcal {F}}\{[{\widetilde {\overline {R}}}(f_{x},f_{y})\otimes {\widetilde {\Psi }}(f_{x},f_{y})]G(f_{x},f_{y})\}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/415e6afddd07a9f1d5851a84b9d67e5be3c5578f)

![{\displaystyle I_{Reconstruido}={\mathcal {F}}\{{\widetilde {I}}_{\Sigma }(f_{x},f_{y})\}\otimes {\mathcal {F}}\{G(f_{x},f_{y})\}+[{\mathcal {F}}\{{\widetilde {R}}(f_{x},f_{y})\}{\mathcal {F}}\{{\widetilde {\overline {\Psi }}}(f_{x},f_{y})\}]\otimes {\mathcal {F}}\{G(f_{x},f_{y})\}+[{\mathcal {F}}\{{\widetilde {\overline {R}}}(f_{x},f_{y})\}{\mathcal {F}}\{{\widetilde {\Psi }}(f_{x},f_{y})\}]\otimes {\mathcal {F}}\{G(f_{x},f_{y})\}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/555c93c198d0e1c6230252108e9677ce54ef16d9)