Diferencia entre revisiones de «Fractales»
Sin resumen de edición |
Sin resumen de edición |
||
| Línea 3: | Línea 3: | ||
[http://es.wikipedia.org/wiki/Fractal vea por ejemplo una introducción en wikipedia]. | [http://es.wikipedia.org/wiki/Fractal vea por ejemplo una introducción en wikipedia]. | ||
se han desarrollado fundamentalmente en el plano complejo | Los objetos fractales se han desarrollado fundamentalmente en el plano complejo, es decir, con números que contienen una parte real y una imaginaria. | ||
Un importante grupo de fractales se produce por el mapeo cuadrático. | |||
== mapeo cuadrático == | |||
Se utiliza la iteración | |||
<math>z=z^{2}+c</math> | |||
una y otra vez, donde$<math>c</math> es un punto en el plano complejo. Se realiza | |||
para los distintos puntos del plano complejo y se asocia un valor | |||
a cada punto $c$ dependiendo de su comportamiento con las iteraciones. | |||
Se inicia la iteración con <math>z=0</math>, de manera que los primeros valores | |||
de <math>z</math> son | |||
<math>z_{1} & = & 0\\ | |||
z_{2} & = & c\\ | |||
z_{3} & = & c^{2}+c\\ | |||
z_{4} & = & \left(c^{2}+c\right)^{2}+c</math> | |||
y dado <math>z_{n}</math>, | |||
<math>z_{n+1}=z_{n}^{2}+c</math> | |||
Después de muchas iteraciones se observa si la magnitud del número | |||
complejo <math>z</math> diverge o se mantiene acotada. Se puede mostrar que | |||
para estar acotada la magnitud debe ser menor que 2. Los puntos del | |||
plano complejo que despues de muchas iteraciones no divergen conforman | |||
el \emph{conjunto (en el plano complejo) acotado ante el mapeo cuadrático | |||
(del álgebra de los complejos). }Dicho conjunto también se conoce | |||
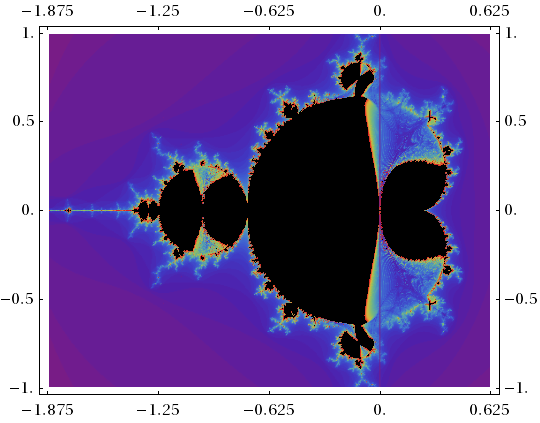
como conjunto de Mandelbrot. | |||
Para encontrarlo se toma como punto inicial ''c'', un punto del | |||
plano complejo y luego otro y asi sucesivamente. A cada punto se le | |||
aplica la iteración cuadrática. La frontera entre los puntos que divergen | |||
y los que no es extremadamente intrincada. Se pueden colorear los | |||
puntos dependiendo de que tan rápido divergen. | |||
Aquí discutiremos los fractales de [[escatores]] ante el mapeo cuadrático. | Aquí discutiremos los fractales de [[escatores]] ante el mapeo cuadrático. | ||
Revisión del 22:10 21 abr 2012
Las estructuras fractales son objetos que exhiben autosimilaridad en distintas escalas. A éstos objetos se les asocia una dimensión fraccionaria, de ahi su nombre. vea por ejemplo una introducción en wikipedia.
Los objetos fractales se han desarrollado fundamentalmente en el plano complejo, es decir, con números que contienen una parte real y una imaginaria.
Un importante grupo de fractales se produce por el mapeo cuadrático.
mapeo cuadrático
Se utiliza la iteración una y otra vez, donde$ es un punto en el plano complejo. Se realiza para los distintos puntos del plano complejo y se asocia un valor a cada punto $c$ dependiendo de su comportamiento con las iteraciones.
Se inicia la iteración con , de manera que los primeros valores de son
Error al representar (error de sintaxis): {\displaystyle z_{1} & = & 0\\ z_{2} & = & c\\ z_{3} & = & c^{2}+c\\ z_{4} & = & \left(c^{2}+c\right)^{2}+c}
y dado ,
Después de muchas iteraciones se observa si la magnitud del número
complejo diverge o se mantiene acotada. Se puede mostrar que
para estar acotada la magnitud debe ser menor que 2. Los puntos del
plano complejo que despues de muchas iteraciones no divergen conforman
el \emph{conjunto (en el plano complejo) acotado ante el mapeo cuadrático
(del álgebra de los complejos). }Dicho conjunto también se conoce
como conjunto de Mandelbrot.
Para encontrarlo se toma como punto inicial c, un punto del plano complejo y luego otro y asi sucesivamente. A cada punto se le aplica la iteración cuadrática. La frontera entre los puntos que divergen y los que no es extremadamente intrincada. Se pueden colorear los puntos dependiendo de que tan rápido divergen.
Aquí discutiremos los fractales de escatores ante el mapeo cuadrático.
El célebre conjunto de Mandelbrot se modifica al conjunto ciolal.
--Manuel-tepal 22:58 9 sep 2007 (CDT)