Diferencia entre revisiones de «Figuras de Lissajous»
| Línea 43: | Línea 43: | ||
== Historia == | == Historia == | ||
El físico | El físico francés Jules Antoine Lissajous presentó a mediados del siglo XIX un informe sobre unas curvas que había estudiado a la luz. Encontró un método para visualizar la curva que generaba la combinación de dos movimientos armónicos simples. | ||
Su | Su método consistía de dos diapasones idénticos con un espejo ligero fijado en el que reflejó un haz de luz, posteriormente, aplicó una vibración con cierta frecuencia a cada diapasón y esta reflexión formaba una figura al ser proyectada, la forma de estas figuras era determinada por la frecuencia de las vibraciones en los diapasones.<ref>https://www.investigacionyciencia.es/revistas/investigacion-y-ciencia/el-nuevo-coronavirus-796/las-figuras-de-lissajous-18475?fbclid=IwAR3NJmfJQAEjtwh1f4VuU-Ef_WCbmYnobUxIxa3yovZ3xlCSkrWIGfbSwRA</ref> | ||
[[Archivo:Lissajous-Apparatus.jpg|miniaturadeimagen|derecha|Jules Antoine Lissajous y su experimento con diapasones]] | [[Archivo:Lissajous-Apparatus.jpg|miniaturadeimagen|derecha|Jules Antoine Lissajous y su experimento con diapasones]] | ||
| Línea 51: | Línea 51: | ||
Lissajous no fue el primero en estudiar este tipo de curvas. En 1815, Nathaniel Bowditch estaba interesado en el movimiento ondulatorio y publicó sus conclusiones en un artículo de la revista de la American Academy of Arts and Science. Sin embargo, no recurrió a diapasones y espejos, como haría después Lissajous, sino que se limitó a utilizar el péndulo.<ref>https://laaventuradelaciencia.blogspot.com/2011/09/el-armonografo.html?fbclid=IwAR2GlpeQvl32IUnM9vaotpWN-ramAAJCxkEba26iay7E5Biyapu-uhBzZ6w}</ref> | Lissajous no fue el primero en estudiar este tipo de curvas. En 1815, Nathaniel Bowditch estaba interesado en el movimiento ondulatorio y publicó sus conclusiones en un artículo de la revista de la American Academy of Arts and Science. Sin embargo, no recurrió a diapasones y espejos, como haría después Lissajous, sino que se limitó a utilizar el péndulo.<ref>https://laaventuradelaciencia.blogspot.com/2011/09/el-armonografo.html?fbclid=IwAR2GlpeQvl32IUnM9vaotpWN-ramAAJCxkEba26iay7E5Biyapu-uhBzZ6w}</ref> | ||
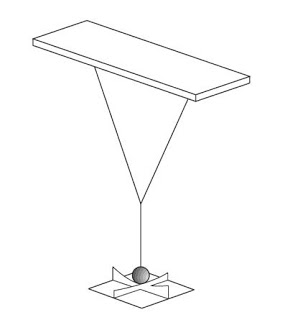
Bowditch cogió un pequeño hilo y lo suspendió por sus dos extremos, fijándolo a una tabla horizontal. Un hilo en cuyo extremo se encontraba una pelota plomiza. De manera que se veía | Bowditch cogió un pequeño hilo y lo suspendió por sus dos extremos, fijándolo a una tabla horizontal. Un hilo en cuyo extremo se encontraba una pelota plomiza. De manera que se veía así: | ||
[[Archivo:Péndulo suspendido de dos hilos.jpg|miniaturadeimagen|centro|El péndulo de Bowditch]] | [[Archivo:Péndulo suspendido de dos hilos.jpg|miniaturadeimagen|centro|El péndulo de Bowditch]] | ||
Revisión del 10:38 19 nov 2020
Introducción
Las figuras de Lissajous, también conocidas como curvas de Bowditch , son el resultado del movimiento de dos osciladores armónicos simples cuyas direcciones son perpendiculares.[1] Si estas dos direcciones las denominamos como X y Y, tendríamos entonces que el movimiento de estos osciladores está descrito por:
$X=A\sin(\omega_x t-\alpha)$ , $Y=B\sin(\omega_y t-\beta)$ , $\delta=\alpha-\beta$
Donde:
$A$ y $B$ son las amplitudes de los osciladores, $\omega_x$ y $\omega_y$ son las frecuencias a las que oscila cada uno y $\delta$ es el ángulo de desfase entre ambos osciladores. Al eliminar la variable de tiempo ($t$) de las expresiones anteriores obtenemos la ecuación paramétrica:
$f(X,Y,\delta)=cte$
que corresponde a la figura de Lissajous.
Propiedades
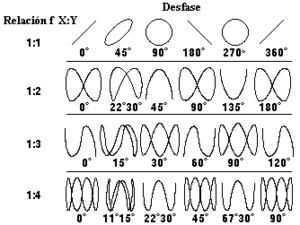
La forma que se observe de la figura de Lissajous dependerá de los 3 parámetros mencionados (amplitud, frecuencia y Angulo de desfase), pero el principal parámetro a considerar es la relación entre ambas frecuencias, ya que está determinará la complejidad de la figura resultante. Si las frecuencias tienen una relación,tal que $\omega_x/\omega_y=1$ entonces tendremos que la figura resultante será una elipse pero dependiendo del ángulo de desfase ($\delta$) se podría observar como un circulo o una línea recta.[2]
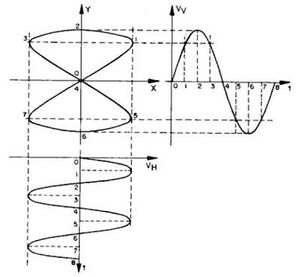
En figuras de Lissajous simples es sencillo determinar la relación entre frecuencias y el ángulo de desfase con solo observar la figura. Para conocer la relación entre frecuencias uno se debe fijar solamente en los puntos máximos de la figura y sus curvas laterales, siendo el numero de curvas laterales que tiene la figura la frecuencia en X ($\omega_x$) y el numero de máximos que tenga su frecuencia en Y ($\omega_y$).
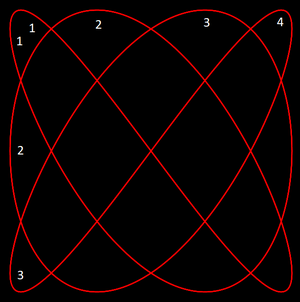
Como ejemplo:
Como se puede observar en la imagen, esta figura tiene 3 curvas laterales y 4 máximos, por lo tanto su relación de frecuencias es de $3/4$. Este método se puede usar cuando la relación entre frecuencias es simple, es decir, que $\omega_x$ y $\omega_y$ sean números enteros. Otro factor a considerar es que si la relacion $\omega_x/\omega_y$ es un numero racional, la figura será cerrada, mientras que si es un numero irracional, la figura será una curva abierta.
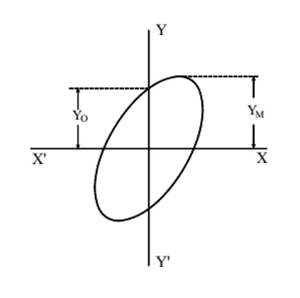
Para conocer el ángulo de desfase se debe tener a la figura centrada en un eje de coordenadas (X,Y).
Como las figuras de Lissajous son ondas senoidales se utilizan las siguientes relaciones:
$Sin\delta=\frac{Y_0}{Y_M}$
$\delta=arcoSin\frac{Y_0}{Y_M}$
Siendo $Y_0$ el valor donde la figura corta el eje Y, $Y_M$ el valor máximo de la curva y $\delta$ el ángulo de desfase.
Historia
El físico francés Jules Antoine Lissajous presentó a mediados del siglo XIX un informe sobre unas curvas que había estudiado a la luz. Encontró un método para visualizar la curva que generaba la combinación de dos movimientos armónicos simples.
Su método consistía de dos diapasones idénticos con un espejo ligero fijado en el que reflejó un haz de luz, posteriormente, aplicó una vibración con cierta frecuencia a cada diapasón y esta reflexión formaba una figura al ser proyectada, la forma de estas figuras era determinada por la frecuencia de las vibraciones en los diapasones.[3]
Lissajous no fue el primero en estudiar este tipo de curvas. En 1815, Nathaniel Bowditch estaba interesado en el movimiento ondulatorio y publicó sus conclusiones en un artículo de la revista de la American Academy of Arts and Science. Sin embargo, no recurrió a diapasones y espejos, como haría después Lissajous, sino que se limitó a utilizar el péndulo.[4]
Bowditch cogió un pequeño hilo y lo suspendió por sus dos extremos, fijándolo a una tabla horizontal. Un hilo en cuyo extremo se encontraba una pelota plomiza. De manera que se veía así:
Este péndulo así construido tenía dos modos de oscilación distintos. Cuando el péndulo oscilaba en una de estas dos direcciones, el resultado no tenía nada de especial. Sin embargo, cuando lo hacia en una dirección oblicua algunas veces el péndulo trazaba una trayectoria circular, en otras elíptica, parabólica o describía una curva con dos ramas. Bodwitch comprendió que había una inmensa variedad de estas curvas o de combinaciones de ellas, y que dependían de las proporciones que las diferentes partes del péndulo mantuviesen entre ellas
Aplicaciones
Algunas de las diversas aplicaciones de las figuras de Lissajous son:
Lectores ópticos: ciertos artefactos como los lectores de precios del supermercado utilizan mecanismos a traves de un haz de luz que genera las figuras de Lissajous lo que permite la lectura del codigo de barras lo cual se reduce a un analisis del precio del producto.
Encriptar datos: algunos datos que son comunicados por fibras ópticas, si alguien desea robarle la señal, no podrá descifrarla con facilidad.
Sonido: Se ha presentado una metodología para lograr trayectorias de fuentes sonoras que siguen esquemas delineados por figuras de Lissajous. Generar patrones de movimiento con figuras de Lissajous es un método ágil para generar trayectorias de sonidos que no son tan predecibles como metodologías lineales o circulares, este modelo ha sido utilizado exitosamente en diversas composiciones.[5]
Análisis de circuitos: Con ayuda del osciloscopio se mide el voltaje pico en cada elemento de un circuito y haciendo uso de las figuras de Lissajous se miden los ángulos de desfase con respecto a la señal de entrada, cuando el ángulo de fase entre ambas señales cambie, la figura de Lissajous variará.[6]
-Cernas Valentin Estefania
-Quinn de Alba Sebastián Alejandro
Referencias
- ↑ https://www.ucm.es/data/cont/docs/76-2013-07-11-05_Lissajous_figures.pdf?fbclid=IwAR1BKgr6TlxdOBcddoScmy6p80y2HWpDIAaTmZAerov5GincvEkGQ0El56A
- ↑ https://www.youtube.com/watch?v=Z4hAtQohON4&feature=youtu.be&fbclid=IwAR2cWQ5G0ttx-zff8PZfUruweEjbMD0rJC0uEzNT4-eaX47yVoUnU8_Gjcg
- ↑ https://www.investigacionyciencia.es/revistas/investigacion-y-ciencia/el-nuevo-coronavirus-796/las-figuras-de-lissajous-18475?fbclid=IwAR3NJmfJQAEjtwh1f4VuU-Ef_WCbmYnobUxIxa3yovZ3xlCSkrWIGfbSwRA
- ↑ https://laaventuradelaciencia.blogspot.com/2011/09/el-armonografo.html?fbclid=IwAR2GlpeQvl32IUnM9vaotpWN-ramAAJCxkEba26iay7E5Biyapu-uhBzZ6w}
- ↑ https://ccrma.stanford.edu/~juanig/papers/motion.pdf?fbclid=IwAR1dxhGbYMCl5qYIAbN8ExoLXVFA9ulrjlv1K_hL63v5LJKmjmShIDH3S5w
- ↑ https://www.academia.edu/7174454/INTRODUCCION_A_LOS_CIRCUITOS?fbclid=IwAR1HT6NecNpGf-BhLhuDm85JJNA3SycPJJgMIv5a-CBsP7tWOc8GrV25qZ8