Determinacion de frecuencias y modos naturales

Métodos para encontrar la frecuencia fundamental aproximada de un sistema compuesto en función de las frecuencias naturales de las partes componentes aplicando la fórmula de Dunkerley.

Principio de Rayleigh y las propiedades del cociente de Rayleigh, así como calcular la frecuencia natural fundamental de un sistema aplicando el método de Rayleigh.

Encontrar las frecuencias naturales aproximadas de vibración y los vectores modales según el método de Holzer.

Determinar las frecuencias mínima, intermedia y máxima de un sistema por medio del método de iteración matricial y sus extensiones (utilizando el procedimiento de deflación matricial).

Fórmula de Dunkerley

Obtendremos el valor aproximado de la $\textbf{frecuencia fundamental}$ de un sistema compuesto en función de las frecuencias naturales de sus partes componentes. Se deriva aprovechando que las altas frecuencias naturales de la mayoría de los sistemas vibratorios son grandes comparadas con sus frecuencias fundamentales.

Para derivar la fórmula de Dunkerley, considere un sistema general de n grados de libertad cuyos valores eigen se pueden determinar resolviendo la ecuación de frecuencia:

\begin{equation} \label{fre} |-[k]+ \omega^2 [m]|= 0 \end{equation}

o

\begin{equation}\label{fre2} \left|-\frac{1}{\omega^2}[I]+[a][m] \right|=0 \end{equation}

En un sistema de masa concentrada con una matriz diagonal, la ecuación $\ref{fre2}$ se escribe como

\begin{equation} \label{matsum} \left|-\frac{1}{\omega^2} \begin{bmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots \\ 0 & 0 & \cdots & 1 \end{bmatrix} + \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix} \begin{bmatrix} m_{1} & 0 & \cdots & 0 \\ 0 & m_{2} & \cdots & 0 \\ \vdots \\ 0 & 0 & \cdots & m_{n} \end{bmatrix} \right| =0 \end{equation}

es decir,

\begin{equation}\label{matsum2} \begin{vmatrix} \left(- \frac{1}{\omega^2} + a_{11}m_{1} \right) & a_{12}m_2 & \cdots & a_{1n}m_n \\ a_{21}m_1 & \left(- \frac{1}{\omega^2} + a_{22}m_{2} \right) & \cdots & a_{2n}m_n\\ \vdots \\ a_{n1}m_1 & a_{n2}m_2 & \cdots & \left(- \frac{1}{\omega^2} + a_{nn}m_{n} \right) \end{vmatrix} =0 \end{equation}

Realizando la expansión de la ecuación $\ref{matsum2}$

\begin{multline} \label{exp} \left(\frac{1}{\omega^2} \right)^n - (a_{11}m_1 + a_{22}m_2 + \cdots + a_{nn} m_n) \left(\frac{1}{\omega^2} \right)^{n-1}\\ + (a_{11} a_{33}m_1 m_3 + \cdots + a_{n-1,n-1} a_{nn}m_{n-1}m_n\\ - a_{12}a_{21}m_1m_2 - \cdots - a_{n-1,n} a_{n,n-1} m_{n-1}m_n) \left(\frac{1}{\omega^2} \right)^{n-2}- \cdots = 0 \end{multline}

Una ecuación polinomial de grado enésimo en $\frac{1}{\omega^2}$. Si las raíces de la ecuación $\ref{exp}$ se indica como $\frac{1}{\omega_{1}^{2}}$ , $\frac{1}{\omega_{2}^{2}}$, $\cdots$, $\frac{1}{\omega_{n}^{2}}$. Por lo tanto

\begin{multline} \label{exp2} \left(\frac{1}{\omega^{2}} -\frac{1}{\omega_{1}^{2}} \right) \left(\frac{1}{\omega^{2}} -\frac{1}{\omega_{2}^{2}} \right) \cdots \left(\frac{1}{\omega^{2}} -\frac{1}{\omega_{n}^{2}} \right)\\ = \left(\frac{1}{\omega^{2}}\right)^n - \left(\frac{1}{\omega_{1}^{2}} + \frac{1}{\omega_{2}^{2}} + \cdots + \frac{1}{\omega_{n}^{2}}\right) \left(\frac{1}{\omega^{2}} \right)^{n-1} - \cdots = 0 \end{multline}

Igualando el coeficiente de $\left(\frac{1}{\omega^{2}} \right)^{n-1}$ en las ecuaciones $\ref{exp2}$ y $\ref{exp}$ se obtiene

\begin{equation}\label{igual} \frac{1}{\omega_{1}^{2}} + \frac{1}{\omega_{2}^{2}} + \cdots + \frac{1}{\omega_{n}^{2}} = a_{11}m_1 + a_{22}m_2 + \cdots + a_{nn} m_n \end{equation}

En la mayoría de los casos las frecuancias altas $\omega_2 , \omega_3, \cdots , \omega_n$ son considerablemente más grandes que la frecuencia fundamental $\omega_1$

\begin{equation*} \frac{1}{\omega_{i}^{2}} \ll \frac{1}{\omega_{1}^{2}}, i= 2,3, \cdots, n \end{equation*}

Por lo tanto la ecuación $\ref{igual}$ se puede escribir aproximadamente como

\begin{equation}\label{igual2} \frac{1}{\omega_{1}^{2}} \simeq a_{11}m_1 + a_{22}m_2 + \cdots + a_{nn} m_n \end{equation}

Esta ecuación se conoce como fórmula de Dunkerley. La frecuencia fundamental que se da en la ecuación $\ref{igual2}$ siempre será menor que el valor exacto. En algunos casos convendrá más volver a escribir la ecuación $\ref{igual2}$ como:

\begin{equation} \frac{1}{\omega_{1}^{2}} \simeq \frac{1}{\omega_{1n}^{2}} + \frac{1}{\omega_{2n}^{2}}+ \cdots + \frac{1}{\omega_{nn}^{2}} \end{equation}

donde $\omega_{in} = ( {1}/{a_{ii}m_i} )^{1/2} = ({k_{ii}}/{m_i})^{1/2} $ indica la frecuencia natural de un sistema de un solo grado de libertad compuesto de la masa $m_i$ y el resorte de rigidez $k_ii, i =1,2, \cdots, n$.

Método de Rayleigh

Este método se puede ampliar para encontrar el valor aproximado de la frecuencia natural fundamental de un sistema discreto (cualquier cuerpo se compone de una estructura discreta o una distribución continua de materia). El método está basado en el principio de Rayleigh, el cual se puede citar como sigue:

La frecuencia de vibración de un sistema conservador vibratorio respecto a una posición de equilibrio tiene en valor estacionario de un modo natural. Este valor estacionario, de hecho, es un valor mínimo en la proximidad del modo natural fundamental.

Resaltando que estacionario no refiere a un estado de reposo, sino a un modo resonante de un objeto extendido vibrante.

\begin{equation} \label{MetRay} T = \frac{1}{2} \int_0^l w^2 dm= \frac{1}{2} w^2 \rho A(x) dx \end{equation}

Derivaremos una expresión para el valor apropiado de la primera frecuencia natural de un sistema de varios grados de libertad de acuerdo con el método de Rayleigh (Ver ecuación $\ref{MetRay}$).

Las energías cinéticas y potencial de un sistema de $n$ grados de libertad se expresan como

\begin{equation} \label{T} T= \frac{1}{2} \dot{x}^T [M] \dot{x} \end{equation}

\begin{equation} \label{V} V= \frac{1}{2} \vec{x}^T [k] \vec{x} \end{equation}

Para enconttrar las frecuencias naturales, suponga que el movimiento armónico es

\begin{equation} \label{x} \vec{x} = \vec{X} \cos \omega t \end{equation}

donde $\vec{X}$ indica el vector de amplitudes (modo de forma) y $\omega$ representa la frecuencia natural de vibración. Si el sistema es conservador, la energía cinética máxima es igual a la energía potencial máxima:

\begin{equation} \label{T-T} T_{máx}= V_{máx} \end{equation}

Sustituyendo la ecuación $\ref{x}$ en las ecuaciones $\ref{T}$ y $\ref{V}$

\begin{equation} \label{Tmax} T_{máx}= \frac{1}{2} \vec{X}^T [m] \vec{X} \omega^2 \end{equation}

\begin{equation} \label{Vmax} V_{máx}= \frac{1}{2} \vec{X}^T [k] \vec{X} \end{equation}

Igualando $T_{máx}=V_{máx}, obtenemos

\begin{equation} \label{w} \omega^2 = \frac{ \vec{X}^T [k] \vec{X} }{ \vec{X}^T [m] \vec{X}} \end{equation}

Y es el lado derecho de la ecuación que se conoce como cociente de Rayleigh y se indica como $R(\vec{X})$.

$\textbf{Propiedades del cociente de Rayleigh }$

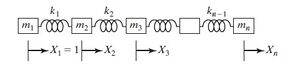
Método de Holzer

El método de Holzer es en esencia un esquema de prueba y error para determinar las frecuencias naturales de sistemas $\textbf{subamortiguados}$, $\textbf{amortiguados}$, $\textbf{semidefinidos}$, fijos, o sistemas vibratorios ramificados que implican desplazamientos lineales y angulares. El método también proporciona los modos.

Fig. 1 Sistema masa resorte con ambos extremos libres

Empezando por el análisis de vibración de sistemas de resorte-masa. Las ecuaciones de movimiento de un sistema de resorte-masa (vea la figura $\textbf{Fig. 1}$) se expresan como

\begin{equation} \label{m1} m_1 \ddot{x_1} + k_1 (x_1 - x_2) = 0 \end{equation}

\begin{equation} \label{m2} m_2 \ddot{x_2} + k_1 (x_2 - x_1) + k_2(x_2 - x_3) = 0 \end{equation}

Para movimiento armónico, $x_i(t) = X_i \cos \omega t$ , donde $X_i$ es la amplitud de la masa m_i y las ecuaciones $\ref{m1}$ y $\ref{m2}$ se escriben como

\begin{equation} \label{wm1} \omega^2 m_1 X_1 = k_1 (x_1 - x_2) \end{equation}

\begin{equation*} \omega^2 m_2 X_2 = k_1 (x_2 - x_1) + k_2(x_2 - x_3) \end{equation*}

\begin{equation} \label{wm2} = - \omega^2 m_1 X_1 + k_2 (X_2 - X_3) \end{equation}

El procedimiento para el método de Holzer se inicia con una frecuencia de prueba \omega y la amplitud de la masa $m_i$ como $X_1=1$. Las ecuaciones $\ref{wm2}$ y $\ref{wm1}$ se pueden utilizar entonces para obtener las amplitudes de las masas $m_2, m_3, \cdots, m_i :$

\begin{equation} \label{X2} X_2 = X_1 - \frac{\omega^2 m_1 X_1}{k_1} \end{equation}

\begin{equation} \label{X3} X_3 = X_2 - \frac{\omega^2}{k^2} (m_1 X_1 + m_2 X_2) \end{equation}

\begin{equation} \label{Xi} X_i = X_{i-1} - \frac{\omega^2}{k_{i-1}} (\sum_{k=1}^{i-1} m_k X_k) \end{equation}

\begin{equation*} i= 2,3, \cdots, n \end{equation*}

La fuerza resultante aplicada a la última masa ($\textit{enésima}$) se calcula como sigue:

\begin{equation} \label{F} F= \sum_{i=1}^{n} \omega^2 m_i X_i \end{equation}

Los cálculos se repiten con otras frecuencias más de prueba $\omega$. Las frecuencias naturales se identifican como aquellos valores de $\omega$ que proporcionan $F=0$ para un sistema con ambos extremos libres. Para ello, es conveniente trazar una gráfica entre $F$ y $\omega$, utilizando el mismo procedimiento para sistemas de resorte-masa que para sistemas $\textbf{torsionales}$.

Método de iteración matricial

Este método asume que las frecuencias naturales son distintas y también separadas de modo que $\omega_1 < \omega_2 < , \cdots , \omega_n$. La iteración se inicia seleccionando un vector de prueba $\vec X_1$, el que luego se premultiplica por la matriz dinámica [D].

El vector columna resultante luego se normaliza, por lo común haciendo que uno de sus componentes sea igual a la unidad. El vector columna normalizado se premultiplica por [D] para obtener un tercer vector columna el cual se normaliza del mismo modo que antes y se convierte en otro vector columna de prueba. El proceso se repite hasta que los vectores columna normalizados sucesivos convergen a un vector común: el vector eigen fundamental.

El factor de normalización presenta el valor máximo de $\lambda = \frac{1}{\omega^2}$, es decir, el valor mínimo de la frecuencia natural fundamental.

La convergencia del proceso se explica como sigue:

De acuerdo con el teorema de expansión, cualquier vector arbitrario de $n$ dimensiones $\vec{X}$ 1 se puede expresar como una combinación lineal de $n$ vectores característicos ortogonales del sistema $\vec{x}(i) , i = 1,2, \cdots , n$

Método de Jacobi

El método produce los valores y vectores característicos de la matriz $[D]$ a la vez. El método de Jacobi también es un método iterativo pero produce todos los valores y vectores característicos de $[D]$ al mismo tiempo, donde $[D] = [d_ij]$ es una matriz simétrica real de orden $n \times n$.

El método está basado en un teorema de álgebra lineal que establece que una matriz simétrica real [D] tiene sólo valores característicos reales y que en ella existe una matriz ortogonal real $[R]$ de modo que $[R]^T[D][R]$ es diagonal.

Los elementos diagonales son los valores característicos, y las columnas de la matriz $[R]$ son los vectores característicos. De acuerdo con el método de Jacobi, la matriz $[R]$ se genera como un producto de varias matrices de rotación de la forma

\begin{equation} [R_1]_{n \times n} \begin{bmatrix} & & & i & & j & & &\\ 1 & 0 & & & & & & &\\ 0 & 1 & & & & & & & \\ & & \ddots & & & & & & \\ & & & \cos{\theta} & & \sin{\theta} & & & \\ & & & & \ddots & & & & \\ & & & \sin{\theta} & & \cos{\theta} & & & \\ & & & & & & \ddots & & \\ & & & & & & & 1 & \end{bmatrix} \end{equation}

donde todos los elementos aparte de los que aparecen en las columnas y filas $i$ y $j$ son idénticos a los de la matriz identidad $[I]$. Si las entradas seno y coseno aparecen en las posiciones $(i, i), (i, j), (j, i)$ y $(j, j)$, entonces los elementos correspondientes de $[R1]^T[D][R1]$ se calculan como sigue:

\begin{equation} \underline{d_{ii}} = d_{ii} \cos^2\theta + 2d_{ij} \sin{\theta} \cos{\theta} + d_{jj} \sin^2 {\theta} \end{equation}

\begin{equation} \underline{d_{ij}} = d_{ji} = (d_{jj} - d_{ii}) \sin{\theta} \cos{\theta} + d_{ij} (\cos^2{\theta} - \sin^2 {\theta}) \end{equation}

\begin{equation} \underline{d_{jj}} = d_{ii} \sin^2\theta - 2d_{ij} \sin{\theta} \cos{\theta} + d_{jj} \cos^2 {\theta} \end{equation}