Compleja:z-ej-cap2.3

La función exponencial y el logaritmo complejo

2.24 Para la recta horizontal ${\mathcal {L}}=\left\{z\epsilon \mathbb {C} :Im(z)=b\right\}$ , demuestre que su imagen bajo la exponencial compleja $exp:\mathbb {C} \rightarrow \mathbb {C} -\left\{0\right\}$ es un rayo basado en el origen quitando el cero.:

Sea $z=a+ib$ y $w=u+iv$

aplicando la exponecial compleja a z nos queda:

$e^{z}=e^{a}(cosb+isenb)$

para hacer el mapeo igualamos: $w=e^{z}$

por lo que las componentes u,v nos quedan:

$u=e^{a}Cos\left(b\right)$ :

$v=e^{a}Sin\left(b\right)$

dividimos la primera entre la segunda ecuación:

${\frac {u}{v}}={\frac {e^{a}Cos\left(b\right)}{e^{a}Sin\left(b\right)}}$ :

${\frac {u}{v}}=Tan(b)$ :

$u=vTan(b)$

como $b=cte$ nos queda una recta con pendiente $Tan(b)$

--Ignacio Peralta Martínez (discusión) 23:11 3 dic 2012 (CST)

2.25 Para la recta vertical ${\mathcal {L}}=\left\{z\epsilon \mathbb {C} :Re(z)=a\right\}$ , demuestre que su imagen bajo la exponencial compleja $exp:\mathbb {C} \rightarrow \mathbb {C} -\left\{0\right\}$ es un circulo con centro en el origen y radio $e^{2a}$

hacemos los primeros pasos del ejercicio anterior:

Sea $z=a+ib$ y $w=u+iv$

aplicando la exponecial compleja a z nos queda:

$e^{z}=e^{a}(cosb+isenb)$

para hacer el mapeo igualamos: $w=e^{z}$

por lo que las componentes u,v nos quedan:

$u=e^{a}Cos\left(b\right)$ :

$v=e^{a}Sin\left(b\right)$

pero ahora en ves de dividir, elevamos al cuadrado y sumamos los lados izquierdos y derechos:

$u^{2}+v^{2}=e^{2a}$

como $a=cte$ es la ecuación de un circulo de radio $e^{a}$ .

--Ignacio Peralta Martínez (discusión) 23:11 3 dic 2012 (CST)

2.27 Demuestre que los ceros de las funciones seno y coseno complejas son los mismos que los de las funciones reales correspondientes.

Demostración:

Para la función seno tenemos

Si $\sin sen(z)={\frac {1}{2i}}(e^{iz}-e^{-iz})=0$ , entonces $e^{iz}=e^{-iz}$ , como $z\in \mathbb {C} ,z=a+bI,a,b\in \mathbb {R}$ , asi

$e^{ai-b}=e^{-ai+b}\Longrightarrow e^{-b}e^{ai}=e^{b}e^{-ai}\Longrightarrow e^{-b}{\big (}cos(a)+isen(a){\big )}=e^{b}{\big (}cos(a)-isen(a){\big )}$

Al separar las partes reales e imaginarias, se obtiene el siguiente sistema de ecuaciones

$e^{-b}sen(a)=-e^{b}sen(a)\Longrightarrow (e^{-b}+e^{b})sen(a)=0\cdots \cdots \cdots \cdots$ (1)

$e^{-b}\cos(a)=e^{b}cos(a)\Longrightarrow (e^{-b}-e^{b})cos(a)=0\cdots \cdots \cdots \cdots$ (2)

De (1) se observa que $e^{-b}+e^{b}\not =0$ , por lo que necesariamente $sen(a)=0\Longrightarrow a=0$ , sustituyendo $a$ en (2) se tiene que

$e^{-b}-e^{b}=0\Longrightarrow e^{-b}=e^{b}\Longrightarrow Ln(e^{-b})=Ln(e^{b})\Longrightarrow -b=b\Longrightarrow b=0\Longrightarrow z=0$

Para la función coseno tenemos

Si $cos(z)={\frac {1}{2}}(e^{iz}+e^{-iz})=0$ , entonces $e^{iz}=-e^{-iz}$ , luego

$e^{ai-b}=-e^{-ai+b}\Longrightarrow e^{-b}e^{ai}=-e^{b}e^{-ai}\Longrightarrow e^{-b}{\big (}cos(a)+isen(a){\big )}=-e^{b}{\big (}cos(a)-isen(a){\big )}$

Al separar las partes reales e imaginarias, se obtiene el siguiente sistema de ecuaciones

$e^{-b}sen(a)=e^{b}sen(a)\Longrightarrow (e^{-b}-e^{b})sen(a)=0\cdots \cdots \cdots \cdots$ (3)

$e^{-b}cos(a)=-e^{b}cos(a)\Longrightarrow (e^{-b}+e^{b})cos(a)=0\cdots \cdots \cdots \cdots$ (4)

De (4) se observa que $e^{-b}+e^{b}\not =0$ , por lo que necesariamente $cos(a)=0\Longrightarrow a={\frac {\pi }{2}}$ , sustituyendo $a$ en (3) se tiene que

$e^{-b}-e^{b}=0\Longrightarrow e^{-b}=e^{b}\Longrightarrow Ln(e^{-b})=Ln(e^{b})\Longrightarrow -b=b\Longrightarrow b=0\Longrightarrow z={\frac {\pi }{2}}$

Por lo tanto, el cero de las fuciones seno y coseno complejas son las mismas que el de las funciónes reales correspondientes.

--Pérez Córdoba Sabino (discusión) 15:47 28 nov 2012 (CST)

2.28 Concluya del ejercicio anterior que las funciones complejas $sen(z)$ y $cos(z)$ , son periódicas con periodos reales de la forma $\tau =2k\pi$ con $k\in \mathbb {Z}$ . Es decir,sus dominios de periocidad son banda verticales de ancho $2\pi$ .

Del ejercicio anterior, se concluyó, para la función seno, que si

sen(z)=0

, con

z=a+bi

, entonces

sen(a)=0

&

b=0

, de donde

a=arcsen(0)=2k\pi ,k\in \mathbb {Z}

, es decir,

$z$ es puramente real, de la forma $z=2k\pi$ , cuyo ancho de banda es $2\pi$ .

Para el caso del coseno, se concluyó que si $cos(a)=0$ , entonces $a=arccos(0)={\frac {\pi }{2}}+2k\pi$ & $b=0$ , nuevamente $z$ es puramente real, de la forma $z={\frac {\pi }{2}}+2k\pi$ . cuyo ancho de banda es $2\pi$

--Pérez Córdoba Sabino (discusión) 16:06 28 nov 2012 (CST)

2.29 Se definen las otras funciones trigonométricas complejas, en términos del seno y coseno complejos, como es usual:

$tan\left({\mathcal {z}}\right)={\frac {sen\left(z\right)}{cos\left(z\right)}}$ ; $sec\left(z\right)={\frac {1}{cos\left(z\right)}},$

$cot\left({\mathcal {z}}\right)={\frac {cos\left(z\right)}{sen\left(z\right)}}$ ; $sec\left(z\right)={\frac {1}{sen\left(z\right)}}.$

Encuentre sus dominios y muestre que son holomorfas en su dominio y sus derivadas son las esperadas.

El dominio del primer par de funciones es todo ${\mathcal {z}}\notin \{{\frac {\pi }{2}}+k\pi \},$

El dominio del segundo par de funciones es todo ${\mathcal {z}}\notin \{k\pi \}.$

Donde $K\in \mathbb {N} .$

Para mostrar que son holomorfas en su dominio, basta demostrar las ecuaciones de Cauchy-Riemann. osea, que son diferenciables en su dominio, lo cual nos genera un intervalo abierto en el cual es diferenciable.

${\mathcal {U}}_{x}={\mathcal {V}}_{y}$ y ${\mathcal {U}}_{y}=-{\mathcal {V}}_{x}.$

sabemos $Tan\left({\mathcal {Z}}\right)=Tan\left({\mathcal {x}}+i{\mathcal {y}}\right)={\frac {Sin\left(2{\mathcal {x}}\right)}{Cos\left(2{\mathcal {x}}\right)+Cosh\left(2{\mathcal {y}})\right)}}+{\frac {iSinh\left(2{\mathcal {y}}\right)}{Cos\left(2{\mathcal {x}}\right)+Cosh\left(2{\mathcal {y}})\right)}}.$

Entonces tenemos que la parte real;

${\mathcal {U}}\left(x,y\right)={\frac {Sen\left(2{\mathcal {x}}\right)}{Cos\left(2{\mathcal {x}}\right)+Cosh\left(2{\mathcal {y}})\right)}},$

y la parte imaginaria es ;

${\mathcal {V}}\left(x,y\right)={\frac {iSenh\left(2{\mathcal {y}}\right)}{Cos\left(2{\mathcal {x}}\right)+Cosh\left(2{\mathcal {y}})\right)}}.$

Comprobemos las ecucuaciones de Cauchy-Riemann.

${\mathcal {U}}_{x}={\frac {\left[cos\left(2{\mathcal {x}}\right)+cosh\left(2{\mathcal {y}}\right)\right]2cos\left(2{\mathcal {x}}\right)-sen\left(2{\mathcal {x}}\right)\left(-2sen\left(2{\mathcal {x}}\right)\right)}{\left[cos\left(2{\mathcal {x}}\right)+cosh\left(2{\mathcal {y}}\right)\right]^{2}}}={\frac {2+2cos\left(2{\mathcal {x}}\right)\left(cosh\left(2{\mathcal {y}}\right)\right)}{\left[cos\left(2{\mathcal {x}}\right)+cosh\left(2{\mathcal {y}}\right)\right]^{2}}}.$

${\mathcal {V}}_{y}={\frac {\left[cos\left(2{\mathcal {x}}\right)+cosh\left(2{\mathcal {y}}\right)\right]2cosh\left(2{\mathcal {y}}\right)-senh\left(2{\mathcal {y}}\right)\left(-2senh\left(2{\mathcal {y}}\right)\right)}{\left[cos\left(2{\mathcal {x}}\right)+cosh\left(2{\mathcal {y}}\right)\right]^{2}}}={\frac {2+2cos\left(2{\mathcal {x}}\right)\left(cosh\left(2{\mathcal {y}}\right)\right)}{\left[cos\left(2{\mathcal {x}}\right)+cosh\left(2{\mathcal {y}}\right)\right]^{2}}}.$

De manera similar obtenemos;

${\mathcal {U}}_{y}={\frac {-sin\left(2{\mathcal {x}}\right)\left[2senh\left(2{\mathcal {y}}\right)\right]}{\left[cos\left(2{\mathcal {x}}\right)+cosh\left(2{\mathcal {y}}\right)\right]^{2}}}=-{\frac {2sen\left(2{\mathcal {x}}\right)senh\left(2{\mathcal {y}}\right)}{\left[cos\left(2{\mathcal {x}}\right)+cosh\left(2{\mathcal {y}}\right)\right]^{2}}}.$

${\mathcal {V}}_{x}={\frac {-sinh\left(2{\mathcal {y}}\right)\left[-2sen\left(2{\mathcal {x}}\right)\right]}{\left[cos\left(2{\mathcal {x}}\right)+cosh\left(2{\mathcal {y}}\right)\right]^{2}}}={\frac {2sen\left(2{\mathcal {x}}\right)senh\left(2{\mathcal {y}}\right)}{\left[cos\left(2{\mathcal {x}}\right)+cosh\left(2{\mathcal {y}}\right)\right]^{2}}}.$

Cumple con las ecuaciones de Cauchy-Riemann, en un intervalo diferenciable, por lo cual es Holomorfa(Analítica).

Ahora comprobemos sus derivadas respecto a z, y veamos que son las esperadas;

$Tan\left({\mathcal {z}}\right)={\frac {sen\left({\mathcal {z}}\right)}{cos(\left({\mathcal {z}}\right)}}$ y entonces Error al representar (error de sintaxis): Tan^´\left(\mathcal{z}\right)=\frac{cos(\left(\mathcal{z}\right)cos(\left(\mathcal{z}\right)-sen\left(\mathcal{z}\right)\left(-sen\left(\mathcal{z}\right)\right)}{\left[cos(\left(\mathcal{z}\right)\right]^2}=\frac{cos^2\left(\mathcal{z}\right)+ sin^2\left(\mathcal{z}\right)}{\left[cos\left(\mathcal{z}\right)\right]^2}= \frac{1}{cos^2\left(\mathcal{z}\right)}= sec^2\left(\mathcal{z}\right).

$Sec\left({\mathcal {z}}\right)={\frac {1}{cos(\left({\mathcal {z}}\right)}}$ y entonces Error al representar (error de sintaxis): Sec^´\left(\mathcal{z}\right)=-\frac{-sen(\left(\mathcal{z}\right)}{\left[cos(\left(\mathcal{z}\right)\right]^2}=\frac{sen\left(\mathcal{z}\right)}{\left[cos\left(\mathcal{z}\right)\right]^2}= \frac{tan\left(\mathcal{z}\right)}{cos\left(\mathcal{z}\right)}= tan\left(\mathcal{z}\right)sec\left(\mathcal{z}\right).

$Cot\left({\mathcal {z}}\right)={\frac {cos\left({\mathcal {z}}\right)}{sen(\left({\mathcal {z}}\right)}}$ y entonces Error al representar (error de sintaxis): Cot^´\left(\mathcal{z}\right)=\frac{-sen\left(\mathcal{z}\right)sen\left(\mathcal{z}\right)-cos\left(\mathcal{z}\right)\left(cos\left(\mathcal{z}\right)\right)}{\left[sen(\left(\mathcal{z}\right)\right]^2}=\frac{-sen^2\left(\mathcal{z}\right)- cos^2\left(\mathcal{z}\right)}{\left[sen\left(\mathcal{z}\right)\right]^2}= \frac{-1}{sen^2\left(\mathcal{z}\right)}= -csc^2\left(\mathcal{z}\right).

$Csc\left({\mathcal {z}}\right)={\frac {1}{sen(\left({\mathcal {z}}\right)}}$ y entonces Error al representar (error de sintaxis): Csc^´\left(\mathcal{z}\right)=-\frac{-cos(\left(\mathcal{z}\right)}{\left[sen(\left(\mathcal{z}\right)\right]^2}=-\frac{cos\left(\mathcal{z}\right)}{\left[sen\left(\mathcal{z}\right)\right]^2}= -cot\left(\mathcal{z}\right)csc\left(\mathcal{z}\right).

Vemos que sus derivadas son las correspondientes.

--Luis Antonio (discusión) 20:30 1 dic 2012 (CST)

2.31. Las funciones trigonométricas hiperbólicas se definen como sigue $senhz={\frac {1}{2}}(e^{z}-e^{-z})$ : $coshz={\frac {1}{2}}(e^{z}+e^{-z})$ : $tanhz={\frac {senhz}{coshz}}$ : $cothz={\frac {coshz}{senhz}}$ : $sechz={\frac {1}{coshz}}$ : $cschz={\frac {1}{senhz}}.$ :

1. Observe que senhz y coshz son holomorfas en todo C. Encuentre los mayores dominios donde las otras funciones hiperbólicas anteriores son holomorfas

2. Obtenga expresiones para las derivadas de las funciones hiperbólicas.

3. Demuestre las identidades siguientes: $Cosh^{2}z-senh^{2}z=1cosz=coshizisenz=senhiz$ :

4. Demuestre las identidades siguientes: $senh(a+b)=senhacoshb+coshasenhb$

$cosh(a+b)=coshacoshb+senhasenhb$

$cosz=cosxcoshy+isenxsenhy$

$senz=senxcoshy+icosxsenhy$

donde $z=x+iy.$

2.-

 $senhz={\frac {1}{2}}(e^{z}-e^{-z})$

Usando la definición de $senhz$ tenemos:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): (Senhz)´= (\frac{1}{2}(e^z-e^{-z}))´ = \frac{1}{2}\frac{ d(e^z-e^{-z})}{dz} = \frac{1}{2}[e^z+e^{-z}] y por

recordando que $coshz={\frac {1}{2}}[e^{z}+e^{-z}]$

entonces se tiene que Error al representar (error de sintaxis): (Senhz)´= coshz

$coshz={\frac {1}{2}}(e^{z}+e^{-z})$

Procedemos de manera similar, derivando la definición de $coshz$ .

Error al representar (error de sintaxis): (Coshz)´= (\frac{1}{2}(e^z+e^{-z}))´ = \frac{1}{2}\frac{ d(e^z+e^{-z})}{dz} = \frac{1}{2}[e^z-e^{-z}] y por

recordando que $senhz={\frac {1}{2}}[e^{z}-e^{-z}]$

entonces se tiene que Error al representar (error de sintaxis): (Coshz)´= senhz

Para la tangente hiperbólica se tiene,

$tanhz={\frac {senhz}{coshz}}$

Por definición del senhz y coshz podemos obtener:

$tanhz={\frac {senhz}{coshz}}$ = ${\frac {e^{z}-e^{-z}}{e^{z}-e^{-z}}}$

Derivando,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): (tanhz)´ $={\frac {(e^{z}+e{-z})(e^{z}+e^{-z})-(e^{z}-e^{-z})(e^{z}-e^{-z})}{(e^{z}+e^{-z})^{2}}}$

Desarrollando y eliminando términos;

$={\frac {2+2}{(e^{z}+e^{-z})^{2}}}={\frac {4}{(e^{z}+e^{-z})^{2}}}$

Usando el hecho de que $(2coshz)^{2}=(e^{2}+e^{-2})^{2}$ y sustituyendo; se obtiene.

$={\frac {4}{4cos^{2}hz}}={\frac {1}{1cos^{2}hz}}.$

Demostracion: $cothz={\frac {coshz}{senhz}}$

Usando la definición de senhz y coshz se tiene

$Cothz={\frac {e^{z}+e^{-z}}{e^{z}-e^{-z}}}$

Error al representar (error de sintaxis): (cothz)´= \frac{(e^z-e^{-z})(e^z-e^{-z})-(e^z+e^{-z})(e^z+e^{-z})}{(e^z+e^{-z})^2}

Desarrollando y eliminando términos, obtenemos.

$={\frac {-2-2}{(e^{z}-e^{-z})^{2}}}={\frac {-4}{4senh^{2}z}}={\frac {-1}{1senh^{2}z}}$

El último termino se obtuvo utilizando la identidad de senhz.

$sechz={\frac {1}{coshz}}$

${\frac {1}{coshz}}={\frac {1}{frac{e^{z}-e^{-z}}{2}}}={\frac {2}{e^{z}+e^{-z}}}$

Derivando la última expresión tenemos.

$={\frac {-2(e^{z}-e^{-z})}{(e^{z}+e^{-z})^{2}}}$

Usando el hecho de que 2coshz= e^z+e^{-z} y sustituyendo dentro de la ecuación anterior.

$={\frac {-2(e^{z}-e^{-z})}{4cosh^{2}z}}$

$={\frac {-4senhz}{4cosh^{2}z}}={\frac {-tanhz}{coshz}}=-tanhzsechz;dadoque{\frac {1}{coshz}}=sechz.$

$cschz={\frac {1}{senhz}}.$

${\frac {1}{senhz}}={\frac {2}{e^{z}-e^{-z}}}$

Derivando el cschz se tiene que,

Error al representar (error de sintaxis): (cschz)´= \frac{-2(e^z+e^{-z}}{(e^z-e^{-z})^2} =

Usando las identidades de senhz y coshz se tiene:

${\frac {-2(2coshz)}{(2senhz)^{2}}}={\frac {-4coshz}{4senh^{2}z}}={\frac {coshz}{senh^{2}z}}$

4.- Identidades

Demostrar $senh(a+b)=senhacoshb+coshasenhb$

Por definición tenemos que: $senhx={\frac {e^{x}-e^{-x}}{2}}$ y $cosnhy={\frac {e^{y}+e^{-y}}{2}}$

$Senhacoshb+coshasenhb=({\frac {e^{a}-e^{-a}}{2}})({\frac {e^{b}+e^{-b}}{2}})+({\frac {e^{a}+e^{-a}}{2}})({\frac {e^{b}-e^{-b}}{2}})$

$={\frac {1}{4}}(e^{a+b}+e^{a-b}-e^{-a+b}-e^{-a-b}+e^{a+b}-e^{a-b}+e^{-a+b}-e^{-a-b})$

Se eliminan algunos términos y obtenemos,

$={\frac {1}{4}}(2e^{a+b}-2e^{-a-b})={\frac {1}{2}}(e^{a+b}-e^{-a-b}=senh(a+b)$

Demostrar $cosh(a+b)=coshacoshb+senhasenhb$

Usando las definiciones, vemos que:

$coshacoshb+senhasenhb=({\frac {e^{a}+e^{-a}}{2}})({\frac {e^{b}+e^{-b}}{2}})+({\frac {e^{a}-e^{-a}}{2}})({\frac {e^{b}-e^{-b}}{2}})$

$={\frac {1}{4}}(e^{a+b}+e^{a-b}+e^{-a+b}+e^{-a-b}+e^{a+b}-e^{a-b}-e^{-a+b}+e^{-a-b})$

Se eliminan algunos términos y obtenemos,

$={\frac {1}{4}}(2e^{a+b}+2e^{-(a+b)})={\frac {1}{2}}(e^{a+b}+e^{-(a+b)}=cosh(a+b)$

$senhz=cosxcoshy+isenxsenhy$

Sea $z=x+iy$

$senhz={\frac {e^{i(x+iy)}-e^{-i(x+iy)}}{2i}}={\frac {e^{xi-y}-e^{-xi+y}}{2i}}$

$={\frac {e^{-y}}{2i}}(cosx+isenx)-{\frac {e^{y}}{2i}}(cosx-isenx)$

$=senx({\frac {e^{-y}+e^{y}}{2}})+icosx({\frac {e^{-y}-e^{y}}{2}})$

Y por definición del $senh$ y $cosh$ se tiene:

$=senxcoshy+icosxsenhy$

$senhz=senxcoshy+icosxsenhy$

Por demostrar.

$Coshz=cosxcoshy-isenxsenhy.$

Sea $z=x+iy$

$coshz={\frac {e^{i(x+iy)}+e^{-i(x+iy)}}{2i}}={\frac {e^{xi-y}+e^{-xi+y}}{2i}}$

$={\frac {e^{-y}}{2i}}(cosx+isenx)-{\frac {e^{y}}{2i}}(cosx-isenx)$

$=cosx({\frac {e^{-y}+e^{y}}{2}})+isenx({\frac {e^{-y}-e^{y}}{2}})$

Y por definición del $senh$ y $cosh$ se tiene:

$=cosxcoshy+isenxsenhy$

$\therefore$ $coshz=cosxcoshy+isenxsenhy$

--Jean Carlo Cruz Venegas (discusión) 07:10 29 nov 2012 (CST)

2.34. Muestre que la imagen bajo la exponencial de la recta $z=(1+i)t$ , para $t\epsilon \mathbb {R}$ es una espiral logarítmica y bosqueje su imagen. Sea $w=re^{i\theta }$ entonces

$w=\mid r\mid (cos\theta +isen\theta )$

hacemos a $w=e^{z}$ entonces

$e^{t}(cost+isent)=\mid r\mid (cos\theta +isen\theta )$ con lo que comparamos y nos queda la solución

$z=log\mid r\mid +\theta i$

nota: la parte imaginaria de z en realidad se le suma $2\pi k$ donde k es cualquier entero.

Para el bosquejo simplemente se sustituye el valor de z en la exponencial compleja, y al pasarlas al plano uv, se puede graficar la espiral al darle valores a las siguientes componentes.

$u=e^{t}cost$

$v=e^{t}sint$

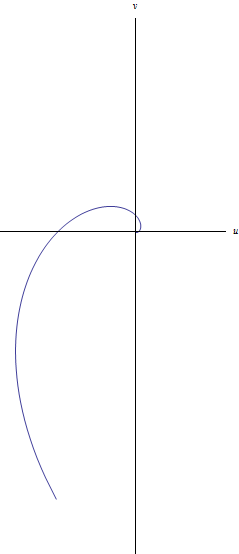
--Ignacio Peralta Martínez (discusión) 05:17 29 nov 2012 (CST)

2.35. Muestre que la función $u$ del ejemplo 2.9 no tiene una conjugada armónica.

El ejemplo al cuál se hace referencia es $u(x,y)=e^{x}seny.$

--Jean Carlo Cruz Venegas (discusión) 12:53 29 nov 2012 (CST)

2.37 Demuestre que las ecucaciones de Laplace tienen la forma en coordenadas polares:

r^{2}{\frac {\partial ^{2}u}{\partial r^{2}}}+r{\frac {\partial u}{\partial r}}+{\frac {\partial ^{2}u}{\partial \theta ^{2}}}=0

${\frac {\partial u}{\partial r}}={\frac {1}{r}}{\frac {\partial v}{\partial \theta }}\Rightarrow {\frac {\partial v}{\partial \theta }}=r{\frac {\partial u}{\partial r}}\land {\frac {\partial v}{\partial r}}=-{\frac {1}{r}}{\frac {\partial u}{\partial \theta }}$ entonces:

${\frac {\partial }{\partial r}}({\frac {\partial v}{\partial \theta }})={\frac {\partial ^{2}v}{\partial r\partial \theta }}=r{\frac {\partial ^{2}u}{\partial r\partial \theta }}+{\frac {\partial u}{\partial r}}$

y:

${\frac {\partial }{\partial \theta }}({\frac {\partial v}{\partial r}})={\frac {\partial }{\partial \theta }}(-{\frac {1}{r}}{\frac {\partial u}{\partial \theta }})=-{\frac {1}{r}}{\frac {\partial ^{2}u}{\partial \theta ^{2}}}$

como ${\frac {\partial ^{2}v}{\partial r\partial \theta }}={\frac {\partial ^{2}v}{\partial \theta \partial r}}$ entonces:

$r{\frac {\partial ^{2}v}{\partial r^{2}}}+{\frac {\partial u}{\partial r}}=-{\frac {1}{r}}{\frac {\partial ^{2}u}{\partial \theta ^{2}}}$ $\therefore {\frac {\partial ^{2}u}{\partial r^{2}}}+{\frac {1}{r}}{\frac {\partial u}{\partial r}}+{\frac {1}{r^{2}}}{\frac {\partial ^{2}u}{\partial \theta ^{2}}}=0$

de la misma forma:

${\frac {\partial }{\partial r}}({\frac {\partial u}{\partial \theta }})={\frac {\partial }{\partial r}}(-r{\frac {\partial v}{\partial r}})=-r{\frac {\partial ^{2}v}{\partial r^{2}}}-{\frac {\partial v}{\partial r}}$

como ${\frac {\partial ^{2}u}{\partial \theta \partial r}}={\frac {\partial ^{2}u}{\partial r\partial \theta }}$ entonces:

${\frac {1}{r}}{\frac {\partial ^{2}v}{\partial \theta ^{2}}}=-r{\frac {\partial ^{2}v}{\partial r^{2}}}-{\frac {\partial v}{\partial r}}$

$\therefore r^{2}{\frac {\partial ^{2}u}{\partial r^{2}}}+r{\frac {\partial u}{\partial r}}+{\frac {\partial ^{2}u}{\partial \theta ^{2}}}=0$

--Cesar (discusión) 10:34 29 nov 2012 (CST)

2.38) Demuestre que si v es conjugado armónica de u, entonces las funciones uv y $x^{2}-y^{2}$ son armónicas.

Demostración Si v es la conjugada armónica de u, u es armónica en $\mathbb {C}$ , entonces Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} \\ Error al representar (error de sintaxis): \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}\\ entonces: Error al representar (error de sintaxis): \frac{\partial^2 u}{\partial x^2} = \frac{\partial^2 v}{\partial y \partial x} \\ y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{\partial^2 u}{\partial y^2} = -\frac{\partial^2 v}{\partial x \partial y}\\ $\therefore$ Error al representar (error de sintaxis): \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} \\ =0

$Seau(x,y)=x^{2}-y^{2}$ , entonces: Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): \frac{\partial v}{\partial x} =2y\\ y Error al representar (error de sintaxis): \frac{\partial v}{\partial y} = 2x \\ integrando con respecto a x, tenemos: v(x,y)=2xy +C entonces: $v(x,y)=2xy+g_{1}$ y $v(x,y)=2xy+g_{2}$