La esfera de Riemann y el plano extendido
1.67. Usando la proyección estereográfica demuestre que la proyección de un círculo S en  corresponde a un círculo T en el plano
corresponde a un círculo T en el plano  . Demuestre que si S contiene al polo norte, entonces su proyección T en
. Demuestre que si S contiene al polo norte, entonces su proyección T en  es una recta.
es una recta.
Un círculo en S en  es la intersección de un plano con la esfera, por lo que sus puntos satisfacen una ecuación de la forma
es la intersección de un plano con la esfera, por lo que sus puntos satisfacen una ecuación de la forma  .
.
Por tanto este círculo es la imagen bajo la proyección estereográfica (2), satisfaciendo

donde  por tanto
por tanto 



Si  , tenemos
, tenemos
 , i.e.,
, i.e.,  , la ecuación de una recta.
, la ecuación de una recta.
Si  , completando cuadrados:
, completando cuadrados:
 .
.
 .
.
 , la ecuación de un círculo con centro en
, la ecuación de un círculo con centro en  y radio
y radio  .
.
--Belen (discusión) 22:51 22 nov 2012 (CST)
1.71.Si  ,
, , demuestre que
, demuestre que
 .
.
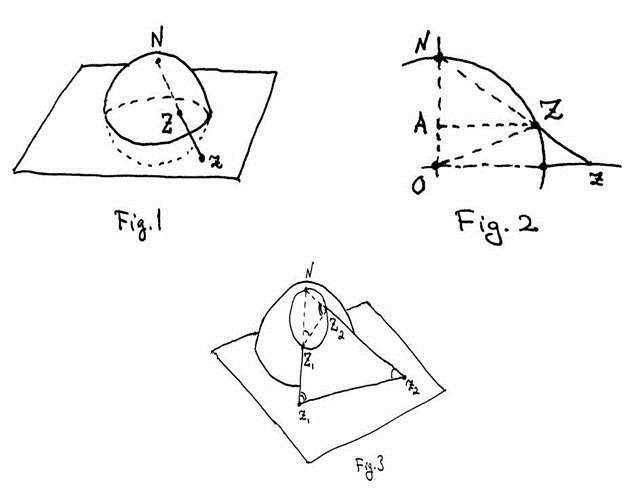
Sea  ,
,
Por triángulos semejantes  y
y
 , implica
, implica  .
.
Pero y
y  , entonces
, entonces
 y
y 
El plano N_z1z2, intersecta a S en un circulo, .
.
Vemos que ,
,
los triangulos N_z1z2 y N_Z1Z2, son semejantes, entonces;

Hacemos
--Luis Antonio (discusión) 09:39 28 nov 2012 (CST)
--mfg-wiki (discusión) 17:32 15 nov 2012 (UTC)
Compleja:z-ej-cap1.0
Compleja:z-ej-cap1.1
Compleja:z-ej-cap1.2
Compleja:z-ej-cap1.3


































