Diferencia entre revisiones de «Compleja:z-ej-cap1.1»
Sin resumen de edición |
Sin resumen de edición |
||
| (No se muestran 25 ediciones intermedias de 2 usuarios) | |||
| Línea 2: | Línea 2: | ||
'''1.13''' Demuestre que las raíces n-ésimas de z=1 (diferentes de 1) satisfacen la ecuación ciclotómica: | '''1.13''' Demuestre que las raíces n-ésimas de z=1 (diferentes de 1) satisfacen la ecuación ciclotómica: | ||
<math>u^{n-1}+u^{n-2}+.....+u+1=0.</math> | <math>u^{n-1}+u^{n-2}+.....+u+1=0.</math> | ||
'''Demostración''' | |||
Sea <math>u\in\mathbb{C}</math>, se observa que: | Sea <math>u\in\mathbb{C}</math>, se observa que: | ||
<math>1-u^n=(u^{n-1}+u^{n-2}+.....+u+1)(1-u)</math> | <math>1-u^n=(u^{n-1}+u^{n-2}+.....+u+1)(1-u)</math> | ||
entonces: | entonces: | ||
<math>u^{n-1}+u^{n-2}+.....+u+1=\frac{1-u^n}{1-u}</math> | <math>u^{n-1}+u^{n-2}+.....+u+1=\frac{1-u^n}{1-u}</math> | ||
De la última ecuación se | por lo que las raíces de la ecuación ciclotómica son las mismas que las de la ecuación <math>\displaystyle\frac{1-u^n}{1-u}=0</math> | ||
De la última ecuación se observa que <math>1-u\neq0</math>, luego <math>1-u^n=0</math>, es decir, <math>u=\displaystyle{\sqrt[n]{1}}</math>, con <math>u\neq1</math> | |||
Por lo tanto, las n-ésimas raices de <math>z=1</math>, diferentes de 1, satisfacen la ecuación ciclotómica. | Por lo tanto, las n-ésimas raices de <math>z=1</math>, diferentes de 1, satisfacen la ecuación ciclotómica. | ||
--[[Usuario:Sabino|Pérez Córdoba Sabino]] ([[Usuario discusión:Sabino|discusión]]) 12:43 4 dic 2012 (CST) | |||
---- | |||
Realizado por: [[Usuario:Sabino|Pérez Córdoba Sabino]] ([[Usuario discusión:Sabino|discusión]]) 12:43 4 dic 2012 (CST) | |||
---- | ---- | ||
1.16.- ''' Demuestre que un | 1.16.- ''' Demuestre que un semi plano abierto es un conjunto abierto.''' | ||
''' | |||
Demostración | '''Demostración''' | ||
Tenemos <math> P \in B(P_{0}) </math> del cual <math>P_{0}=(x_{0},y_{0})</math>. Decimos que <math> P_{0} \in B , y_{0}>0 </math>. Elegimos un <math> r = y_{0} </math> | Tenemos <math> P \in B(P_{0}) </math> del cual <math>P_{0}=(x_{0},y_{0})</math>. Decimos que <math> P_{0} \in B , y_{0}>0 </math>. Elegimos un <math> r = y_{0} </math> | ||
| Línea 35: | Línea 40: | ||
<math> \therefore </math> <math> y > 0</math>. | <math> \therefore </math> <math> y > 0</math>. | ||
--[[Usuario:Jean Carlo Cruz Venegas|Jean Carlo Cruz Venegas]] ([[Usuario discusión:Jean Carlo Cruz Venegas|discusión]]) 08:20 29 nov 2012 (CST) | |||
---- | |||
Realizado por: [[Usuario:Jean Carlo Cruz Venegas|Jean Carlo Cruz Venegas]] ([[Usuario discusión:Jean Carlo Cruz Venegas|discusión]]) 08:20 29 nov 2012 (CST) | |||
---- | ---- | ||
| Línea 44: | Línea 51: | ||
(b) <math> \Omega </math> es cerrado si y sólo si <math> \Omega^{-} = \Omega </math>.''' | (b) <math> \Omega </math> es cerrado si y sólo si <math> \Omega^{-} = \Omega </math>.''' | ||
'''Inciso a''' | |||
(a) Si <math> \Omega </math> es abierto, entonces para cada z ∈ <math> \Omega </math> existe un <math> \epsilon > 0 </math> tal que <math> B (x,\epsilon) \subset \Omega </math>. Vemos que la unión de todas las bolas <math> B (x,\epsilon) </math> es <math> \Omega </math>. Además, esta unión es igual al interior de <math> \Omega </math> a saber, <math> \Omega^{0} </math>, puesto que para cualquier subconjunto abierto <math>A</math> de <math> \Omega </math> se tiene que | (a) Si <math> \Omega </math> es abierto, entonces para cada z ∈ <math> \Omega </math> existe un <math> \epsilon > 0 </math> tal que <math> B (x,\epsilon) \subset \Omega </math>. Vemos que la unión de todas las bolas <math> B (x,\epsilon) </math> es <math> \Omega </math>. Además, esta unión es igual al interior de <math> \Omega </math> a saber, <math> \Omega^{0} </math>, puesto que para cualquier subconjunto abierto <math>A</math> de <math> \Omega </math> se tiene que $ A \subset \bigcup \left \{ B(x,\epsilon) : x ∈ A \right \} $ Luego <math> \Omega^{0} = \Omega </math>. | ||
Por otro lado, si <math> \Omega^{0} = \Omega </math>, entonces <math> \Omega </math> es abierto por que <math> \Omega ^{0}</math> es abierto. | Por otro lado, si <math> \Omega^{0} = \Omega </math>, entonces <math> \Omega </math> es abierto por que <math> \Omega ^{0}</math> es abierto. | ||
'''Inciso b''' | |||
(b) Si <math> \Omega </math> es cerrado, entonces <math> \bigcap \left \{ A : A \mbox{ es cerrado y } A \supset \Omega \right \} = \Omega^{-} = \Omega </math>, por que <math> \Omega </math> es el | (b) Si <math> \Omega </math> es cerrado, entonces <math> \bigcap \left \{ A : A \mbox{ es cerrado y } A \supset \Omega \right \} = \Omega^{-} = \Omega </math>, por que <math> \Omega </math> es el super conjunto cerrado más pequeño de <math> \Omega </math>. | ||
Por otra parte, si <math> \Omega^{-} = \Omega </math> entonces <math> \Omega </math> es cerrado debido a que <math> \Omega^{-} </math> es cerrado por definición. | Por otra parte, si <math> \Omega^{-} = \Omega </math> entonces <math> \Omega </math> es cerrado debido a que <math> \Omega^{-} </math> es cerrado por definición. | ||
--[[Usuario:Belen|Belen]] ([[Usuario discusión:Belen|discusión]]) 21:11 30 oct 2012 (UTC) | ---- | ||
Realizado por: [[Usuario:Belen|Belen]] ([[Usuario discusión:Belen|discusión]]) 21:11 30 oct 2012 (UTC) | |||
---- | ---- | ||
| Línea 64: | Línea 73: | ||
(b) <math> \Omega ^{-} = \mathbb{C} - ( \mathbb{C} - \Omega ) ^{0} </math>. | (b) <math> \Omega ^{-} = \mathbb{C} - ( \mathbb{C} - \Omega ) ^{0} </math>. | ||
(c) | (c) $ ∂ \Omega = \Omega^{-} - \Omega ^{0} $. | ||
(d) $ ∂ \Omega = \Omega^{-} \bigcap ( \mathbb{C} - \Omega ) ^{-} $. | |||
'''Inciso a''' | |||
(a) | (a) | ||
| Línea 81: | Línea 90: | ||
*P.D. <math> \Omega ^{0} \subseteq \mathbb{C} - ( \mathbb{C} - \Omega ) ^{-} </math> | *P.D. <math> \Omega ^{0} \subseteq \mathbb{C} - ( \mathbb{C} - \Omega ) ^{-} </math> | ||
Sea | Sea $x \in (\mathbb{C} - \Omega )^{-}$, entonces $x \in \mathbb{C} - \Omega$ por que $\mathbb{C} - \Omega \subseteq ( \mathbb{C} - \Omega )^{-}$. | ||
Como | Como $ x ∈ \mathbb{C} - \Omega $, se tiene que $ x ∉ \Omega $ y también que $ x ∉ \Omega ^{0}$ ya que $\Omega ^{0} \subseteq \Omega $. | ||
Puesto que | Puesto que $x \notin \Omega^{0} \Rightarrow x \in \mathbb{C} - \Omega ^{0}$, es decir, al complemento del interior de $\Omega$. | ||
Tenemos entonces que <math> ( \mathbb{C} - \Omega ) ^{-} \subseteq \mathbb{C} - \Omega ^{0}</math>, de donde <math> \Omega ^{0} \subseteq \mathbb{C} - ( \mathbb{C} - \Omega ) ^{-}</math>. | Tenemos entonces que <math> ( \mathbb{C} - \Omega ) ^{-} \subseteq \mathbb{C} - \Omega ^{0}</math>, de donde <math> \Omega ^{0} \subseteq \mathbb{C} - ( \mathbb{C} - \Omega ) ^{-}</math>. | ||
*Ya que <math> \mathbb{C} - ( \mathbb{C} - \Omega ) ^{-} \subseteq \Omega ^{0} </math> y <math> \Omega ^{0} \subseteq \mathbb{C} - ( \mathbb{C} - \Omega ) ^{-}</math>, podemos decir que <math> \Omega ^{0} = \mathbb{C} - ( \mathbb{C} - \Omega ) ^{-} </math>. | *Ya que <math> \mathbb{C} - ( \mathbb{C} - \Omega ) ^{-} \subseteq \Omega ^{0} </math> y <math> \Omega ^{0} \subseteq \mathbb{C} - ( \mathbb{C} - \Omega ) ^{-}</math>, podemos decir que <math> \Omega ^{0} = \mathbb{C} - ( \mathbb{C} - \Omega ) ^{-} </math>. | ||
'''Inciso b''' | |||
(b) | (b) | ||
| Línea 100: | Línea 111: | ||
Y así <math> \Omega^{-} = \mathbb{C} - (\mathbb{C} - \Omega) ^{0}</math>. | Y así <math> \Omega^{-} = \mathbb{C} - (\mathbb{C} - \Omega) ^{0}</math>. | ||
'''Inciso c''' | |||
(c) | (c) | ||
Tenemos que <math> x | Tenemos que <math> x \in \partial \ \Omega \Leftrightarrow x \in [ \Omega \cap ( \mathbb{C} - \Omega ) ] </math>. | ||
<math> \Leftrightarrow x \in [ \Omega^{-} \cap ( \mathbb{C} - \Omega )^{-} ] </math> (puesto que <math> \Omega \subseteq \Omega ^{-} </math>) | |||
<math> \Leftrightarrow x | <math> \Leftrightarrow x \in \Omega^{-} </math> y <math> x \in (\mathbb{C} - \Omega) ^{-} </math> | ||
<math> \Leftrightarrow x | <math> \Leftrightarrow x \in \Omega^{-} </math> y <math> x \notin \mathbb{C} - (\mathbb{C} - \Omega) ^{-} = \Omega ^{0}</math> (por el inciso anterior) | ||
<math> \Leftrightarrow x | <math> \Leftrightarrow x \in ( \Omega^{-} - \Omega ^{0} ) </math>. | ||
'''Inciso d''' | |||
(d) | (d) | ||
Veamos a la frontera <math> | Veamos a la frontera <math> \partial \Omega </math> como el conjunto de puntos que NO están en el interior <math> \Omega ^{0} </math> ni en el exterior (la unión de todos los abiertos ajenos con <math> \Omega </math>, es decir, la unión de todos los abiertos contenidos en <math> \mathbb{C} - \Omega </math>). El exterior de <math>\Omega</math> es el interior de <math> \mathbb{C} - \Omega </math>, o sea el conjunto <math> ( \mathbb{C} - \Omega ) ^{0} </math>. | ||
Así, <math> | Así, <math> \partial \Omega = \mathbb{C} - [ \Omega ^{0} \cup ( \mathbb{C} - \Omega ) ^{0} ] = \mathbb{C} - \Omega ^{0} \cap \mathbb{C}- (\mathbb{C} - \Omega ) ^{0}</math> | ||
Sabemos del inciso (a) que <math> \Omega ^{0} = \mathbb{C} - ( \mathbb{C} - \Omega ) ^{-} </math> y del inciso (b) que <math> \Omega^{-} = \mathbb{C} - (\mathbb{C} - \Omega) ^{0}</math>. | Sabemos del inciso (a) que <math> \Omega ^{0} = \mathbb{C} - ( \mathbb{C} - \Omega ) ^{-} </math> y del inciso (b) que <math> \Omega^{-} = \mathbb{C} - (\mathbb{C} - \Omega) ^{0}</math>. | ||
| Línea 123: | Línea 138: | ||
De tal forma que <math> \mathbb{C} - \Omega ^{0} \cap \mathbb{C}- (\mathbb{C} - \Omega ) ^{0} = ( \mathbb{C} - \Omega ) ^{-} \cap \Omega^{-} </math>. | De tal forma que <math> \mathbb{C} - \Omega ^{0} \cap \mathbb{C}- (\mathbb{C} - \Omega ) ^{0} = ( \mathbb{C} - \Omega ) ^{-} \cap \Omega^{-} </math>. | ||
--[[Usuario:Belen|Belen]] ([[Usuario discusión:Belen|discusión]]) 02:37 31 oct 2012 (UTC) | ---- | ||
Realizado por: [[Usuario:Belen|Belen]] ([[Usuario discusión:Belen|discusión]]) 02:37 31 oct 2012 (UTC) | |||
---- | ---- | ||
'''1.21 Sea <math> \Omega \subseteq \mathbb{C} </math>. Demuestre que:''' | '''1.21 Sea <math> \Omega \subseteq \mathbb{C} </math>. Demuestre que:''' | ||
'''Inciso a''' | |||
(a) <math>z \in \Omega ^{0}</math> si y sólo si existe <math> \epsilon > 0 </math> tal que <math> B(z; \epsilon) \subseteq \Omega </math>. | |||
( | Si <math>z \in \Omega ^{0}</math> entonces existe un <math> \epsilon > 0 </math> tal que <math> B(z; \epsilon) \subseteq \Omega ^{0}</math>, por que <math>\Omega ^{0}</math> es abierto. Como <math>\Omega ^{0} \subseteq \Omega</math>, resulta que <math> B(z; \epsilon) \subseteq \Omega </math>. En la otra dirección, si <math> B(z; \epsilon) \subseteq \Omega </math> para algún <math> \epsilon > 0 </math>, entonces por ser <math> B(z; \epsilon) </math> un conjunto abierto, se tiene que <math>z \in \Omega ^{0}</math>, por que <math> \Omega ^{0}</math> es la unión de todos los subconjuntos abiertos de <math> \Omega </math> | ||
'''Inciso b''' | |||
(b) <math>z \in \Omega ^{-}</math> si y sólo si para todo <math> \epsilon > 0 </math> se tiene que <math> B(z; \epsilon) \cap \Omega \ne \emptyset </math> | |||
Supóngase que <math>z \in \Omega ^{-}</math>, por 1.20 (b) <math>z \in (\mathbb{C} - ( \mathbb{C} - \Omega ) ^{0})</math> y de este modo <math>z \notin ( \mathbb{C} - \Omega ) ^{0}</math>. Con esto y por el inciso anterior, se obtiene que para cada <math> \epsilon > 0 </math>, <math> B(z; \epsilon) \nsubseteq (\mathbb{C} - \Omega) </math>. De esta forma, para cada <math> \epsilon > 0 </math> hay un punto <math> w \in B(z; \epsilon) </math> que no pertenece a <math> (\mathbb{C} - \Omega) </math>, con lo cual <math> w \in \Omega </math>, y así <math> w \in ( B(z; \epsilon) \cap \Omega ) </math>. Ahora supóngase que <math>z \notin \Omega ^{-} = \mathbb{C} - ( \mathbb{C} - \Omega ) ^{0}</math>, entonces <math>z \in ( \mathbb{C} - \Omega ) ^{0}</math>, y por el inciso anterior existe un <math> \epsilon > 0 </math> tal que <math> B(z; \epsilon) \subseteq (\mathbb{C} - \Omega) </math>. De esto se obtiene que <math> B(z; \epsilon) \cap \Omega \ne \emptyset </math>. | |||
---- | |||
Realizado por: [[Usuario:Ricardo velasco bazán|Ricardo velasco bazán]] ([[Usuario discusión:Ricardo velasco bazán|discusión]]) 02:41 6 nov 2012 (UTC) | |||
---- | |||
'''<math>\ | '''1.22 Sea <math>\Omega\subseteq\mathbb{C}</math> cualquier conjunto muestre que:''' | ||
'''Ejercicio 1''' | |||
<math>\left(1\right)</math> | |||
'''Inciso a''' | |||
'''<math>\left( | '''<math>\left(a\right)</math> <math>\Omega</math> es abierto relativo en <math>\Omega</math>.''' | ||
'' | ''Puesto que dice que <math>\Omega</math> puede ser cualquier conjunto, lo escogemos abierto, entonces <math>\Omega</math> será abierto relativo tal que exista un <math>\mathcal{A}_1\subseteq\Omega\subseteq\mathbb{C}</math>, tal que <math>\mathcal{A}_1 \cap\Omega =\Omega.</math>'' | ||
''Dado que <math>\Omega</math> contiene a <math>\mathcal{A}_1</math>, entonces cumple con la primera parte del parrafo 1 del texto en la pagina 17.'' | |||
''' | '''Inciso b''' | ||
'''<math>\left(b\right)</math>Si <math>\mathcal{A}_1</math>,.....,<math>\mathcal{A}_n\subseteq\Omega</math> son abiertos relativos, <math>\mathcal{A}_1\cap.....\cap \mathcal{A}_n</math> es abierto relativo.''' | |||
''Veamos, por el inciso<math>\left(a\right)</math>, hemos dicho que <math>\mathcal{A}_1\subseteq\Omega</math>, tal que <math>\mathcal{A}_1\cap\Omega =\Omega</math>, esto quiere decir que podemos tomar <math>\mathcal{A}_1,.....,\mathcal{A}_n\subseteq\Omega</math>, tal que <math>\left(\mathcal{A}_1\cap,.....,\cap\mathcal{A}_n\right)\cap\Omega = \Omega</math>, por lo cual se sigue cumpliendo que esa intersección de conjuntos abiertos generan a un abierto relativo.'' | |||
'''Inciso c''' | |||
'''<math>\left(c\right)</math>Si <math>\lbrace{A_k\rbrace}</math> es cualquier familia de subconjuntos de <math>\Omega</math> que son abiertos relativos, entonces <math>\bigcup_k A_k</math> también es abierto relativo.''' | |||
<math>\left( | ''Hemos mostrado en <math>\left(b\right)</math> que <math>\{\cap\mathcal{A}_k\}\subseteq\Omega =\Omega</math>, y es abierto relativo por <math>\left(a\right)</math>, ahora tenemos <math>\{\cup\mathcal{A}_k\}</math>, tal que por ser abiertos y su unión es <math>\{\cup\mathcal{A}_k\}\cap\Omega =\Omega</math>, lo cual sigue generando a nuestro abierto relativo.'' | ||
'''Ejercicio 2''' | |||
<math>\left(2\right)</math> | |||
''' | '''Inciso a''' | ||
'''<math>\left(a\right)</math> <math>\Omega</math> es cerrados relativo en <math>\Omega</math>.''' | |||
''Puesto que dice que <math>\Omega</math> puede ser cualquier conjunto, lo escogemos cerrado, entonces <math>\Omega</math> será cerrado relativo tal que exista un <math>\mathcal{A}_1\subseteq\Omega\subseteq\mathbb{C}</math>, tal que <math>\mathcal{A}_1 \cap\Omega =\Omega.</math>'' | |||
'''Inciso b''' | |||
'''<math>\left(b\right)</math>Si <math>A_1</math>,.....,<math>A_n\subseteq\Omega</math> son cerrados relativos, <math>A_1\cup.....\cup A_n</math> es cerrado relativo.''' | |||
''Entonces, por el inciso<math>\left(a\right)</math>, hemos dicho que <math>\mathcal{A}_1\subseteq\Omega</math>, tal que <math>\mathcal{A}_1\cap\Omega =\Omega</math>, esto quiere decir que podemos tomar <math>\mathcal{A}_1,.....,\mathcal{A}_n\subseteq\Omega</math>, tal que <math>\left(\mathcal{A}_1\cup,.....,\cup\mathcal{A}_n\right)\cap\Omega = \Omega</math>, por lo cual se sigue cumpliendo que esa unión de conjuntos cerrados generan a un cerrado relativo.'' | |||
''' | '''Inciso c''' | ||
''' | '''<math>\left(c\right)</math>Si <math>\lbrace{A_k\rbrace}</math> es cualquier familia de subconjuntos de <math>\Omega</math> que son cerrados relativos, entonces <math>\bigcap_k A_k</math> también es cerrado relativo.''' | ||
''Hemos mostrado en <math>\left(b\right)</math> que <math>\{\cup\mathcal{A}_k\}\subseteq\Omega =\Omega</math>, y es cerrado relativo por <math>\left(a\right)</math>, ahora tenemos <math>\{\cap\mathcal{A}_k\}</math>, tal que por ser cerrados y su unión es <math>\{\cap\mathcal{A}_k\}\cap\Omega =\Omega</math>, lo cual sigue generando a nuestro cerrado relativo.'' | |||
---- | |||
Realizado por: [[Usuario:Luis Antonio|Luis Antonio]] ([[Usuario discusión:Luis Antonio|discusión]]) 16:39 5 dic 2012 (CST) | |||
---- | |||
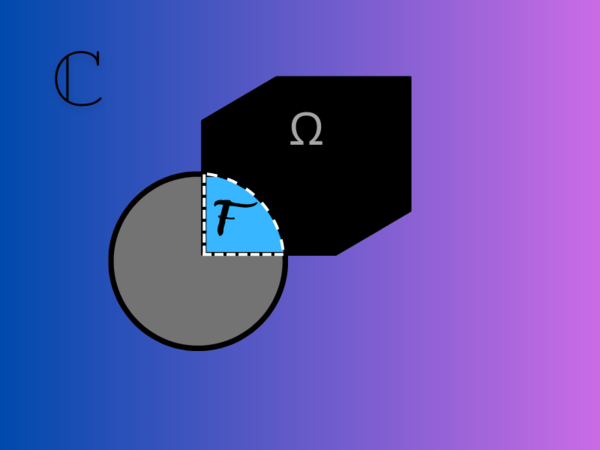
'''<math>A</math> | '''1.23 Si <math>A\subseteq\Omega</math> es abierto relativo, demuestre que <math>\Omega-A\subseteq\Omega</math> es cerrado relativo. Demuestre también que si <math>F\subseteq\Omega</math> es cerrado relativo, entonces <math>\Omega-F\subseteq\Omega </math> es abierto relativo''' | ||
'''* Se dice que un subconjunto abierto <math>\mathcal{A}_1\subseteq\Omega</math> es abierto relativo en <math>\Omega</math> si existe un conjunto abierto <math>\mathcal{A}_1\subseteq\mathbb{C}</math> tal que <math>\Omega=\mathcal{A}_1\cap\Omega</math>.''' | |||
'''* Se dice que un subconjunto cerrado <math>\mathcal{F}_1\subseteq\Omega</math> es cerrado relativo en <math>\Omega</math> si existe un conjunto cerrado <math>\mathcal{F}_1\subseteq\mathbb{C}</math> tal que <math>\Omega=\mathcal{F}_1\cap\Omega</math>.''' | |||
''Lo anterior es por el ejercicio 1.22'' | |||
[[Archivo:Complejaz-ej-cap1.1Conjunto.png|600px|sinmarco|centro]] | |||
'' | ''Podemos imaginar el analisis como el conjunto <math>\Omega</math> es abierto relativo, su <math>\Omega^c = \mathcal{A}_1 -\Omega</math> será cerrado relativo, esto por que <math>\mathcal{A}_1 </math> podrá tocar sus puntos frontera. De manera similar si <math>\Omega</math> es cerrado relativo, por entonces sus complemento <math>\Omega^c = \mathcal{F}_1 -\Omega</math>, será abierto relativo por que <math>\mathcal{F}_1</math> no podrá tocar su frontera.'' | ||
''Entonces se concluye lo que nos pide demostrar el enunciado enuciado.'' | |||
-- | ---- | ||
Realizado por: [[Usuario:Luis Antonio|Luis Antonio]] ([[Usuario discusión:Luis Antonio|discusión]]) 18:08 5 dic 2012 (CST) | |||
---- | ---- | ||
| Línea 228: | Línea 256: | ||
Ahora supóngase que <math>I</math> no es un intervalo, entonces existen dos puntos <math>a,b \in I, a < b </math>, tal que <math> (a,b) \nsubseteq I </math> (un teorema afirma que <math>I</math> es un intervalo si y sólo si para cualquier par de puntos <math>a,b \in I</math>, con <math>a < b </math> se tiene que <math>(a,b) \subset I </math>). Entonces, existe un punto <math> c \notin I </math> tal que <math> a < c < b </math>. Como <math> a \in (- \infty , c ) </math> y <math> b \in ( c, \infty ) </math> se tiene que <math> I = ( I \cap (-\infty , c) ) \cup ( I \cap ( c, \infty ) ) </math>, donde <math> (I \cap ( - \infty, c ) ) </math> y <math> (I \cap (c, \infty)) </math> son conjuntos disjuntos no vacíos. Por lo tanto, <math>I</math> no es conexo. | Ahora supóngase que <math>I</math> no es un intervalo, entonces existen dos puntos <math>a,b \in I, a < b </math>, tal que <math> (a,b) \nsubseteq I </math> (un teorema afirma que <math>I</math> es un intervalo si y sólo si para cualquier par de puntos <math>a,b \in I</math>, con <math>a < b </math> se tiene que <math>(a,b) \subset I </math>). Entonces, existe un punto <math> c \notin I </math> tal que <math> a < c < b </math>. Como <math> a \in (- \infty , c ) </math> y <math> b \in ( c, \infty ) </math> se tiene que <math> I = ( I \cap (-\infty , c) ) \cup ( I \cap ( c, \infty ) ) </math>, donde <math> (I \cap ( - \infty, c ) ) </math> y <math> (I \cap (c, \infty)) </math> son conjuntos disjuntos no vacíos. Por lo tanto, <math>I</math> no es conexo. | ||
--[[Usuario:Ricardo velasco bazán|Ricardo velasco bazán]] ([[Usuario discusión:Ricardo velasco bazán|discusión]]) 03:18 6 nov 2012 (UTC) | ---- | ||
Realizado por: [[Usuario:Ricardo velasco bazán|Ricardo velasco bazán]] ([[Usuario discusión:Ricardo velasco bazán|discusión]]) 03:18 6 nov 2012 (UTC) | |||
---- | |||
'''1.25''' Un subconjunto <math>A\subseteq\mathbb{C}</math> se dice que es convexo si para cualquiera dos puntos <math>z,w\in</math><math>A</math> se tiene que el segmento <math>[z,w]\subseteq</math><math>A</math>. | '''1.25''' Un subconjunto <math>A\subseteq\mathbb{C}</math> se dice que es convexo si para cualquiera dos puntos <math>z,w\in</math><math>A</math> se tiene que el segmento <math>[z,w]\subseteq</math><math>A</math>. | ||
:'''(1)''' Demuestre que cualquier disco abierto o cerrado es convexo. | :'''(1)''' Demuestre que cualquier disco abierto o cerrado es convexo. | ||
| Línea 236: | Línea 265: | ||
:'''(3)''' Demuestre que la intersección de cualquier familia de subconjuntos convexos es convexa. | :'''(3)''' Demuestre que la intersección de cualquier familia de subconjuntos convexos es convexa. | ||
::'''Demostración''' | ::'''Demostración''' | ||
'''Inciso 1''' | |||
'''(1)''' Por definición <math>[z,w]:=</math>{<math>tw+(1-t)z : 0\leq t\leq1</math>} | '''(1)''' Por definición <math>[z,w]:=</math>{<math>tw+(1-t)z : 0\leq t\leq1</math>} | ||
| Línea 280: | Línea 313: | ||
Para el caso del semiplano cerrado basta con cambiar la condición (**). | Para el caso del semiplano cerrado basta con cambiar la condición (**). | ||
--[[Usuario:Sabino|Pérez Córdoba Sabino]] ([[Usuario discusión:Sabino|discusión]]) 19:17 22 nov 2012 (CST) | ---- | ||
Realizado por: [[Usuario:Sabino|Pérez Córdoba Sabino]] ([[Usuario discusión:Sabino|discusión]]) 19:17 22 nov 2012 (CST) | |||
---- | ---- | ||
| Línea 289: | Línea 322: | ||
Tomemos una componente <math>\Omega\text{´}\subseteq\mathbb{\Omega} </math> y un punto <math>z_{0}\epsilon\Omega\text{´} </math>, como <math>z_{0}\epsilon\Omega </math> y <math>\Omega</math> es abierto, existe un disco <math>B(z_{0};r)\subseteq\Omega </math>. Recordando que un subconjunto <math>\Omega\subseteq\mathbb{C} </math> no vacío, se puede descomponer como la unión de subconjuntos conexos (proposición 1.8),tenemos que la unión <math>B(z_{0};r)\cup\Omega\text{´} </math> es conexa; y por el hecho de que un conjunto se puede llenar por subconjuntos y los intersticios que hay entre ellos se llenan con conjuntos más pequeños, debe ser igual a <math>\Omega\text{´} </math>. Con esto se entiende que <math>B(z_{0};r)\subseteq\Omega\text{´} </math> y por tanto <math>\Omega\text{´}</math> es abierto. | Tomemos una componente <math>\Omega\text{´}\subseteq\mathbb{\Omega} </math> y un punto <math>z_{0}\epsilon\Omega\text{´} </math>, como <math>z_{0}\epsilon\Omega </math> y <math>\Omega</math> es abierto, existe un disco <math>B(z_{0};r)\subseteq\Omega </math>. Recordando que un subconjunto <math>\Omega\subseteq\mathbb{C} </math> no vacío, se puede descomponer como la unión de subconjuntos conexos (proposición 1.8),tenemos que la unión <math>B(z_{0};r)\cup\Omega\text{´} </math> es conexa; y por el hecho de que un conjunto se puede llenar por subconjuntos y los intersticios que hay entre ellos se llenan con conjuntos más pequeños, debe ser igual a <math>\Omega\text{´} </math>. Con esto se entiende que <math>B(z_{0};r)\subseteq\Omega\text{´} </math> y por tanto <math>\Omega\text{´}</math> es abierto. | ||
--[[Usuario:Ignacio Peralta Martínez|Ignacio Peralta Martínez]] ([[Usuario discusión:Ignacio Peralta Martínez|discusión]]) 19:02 6 nov 2012 (UTC) | ---- | ||
Realizado por: [[Usuario:Ignacio Peralta Martínez|Ignacio Peralta Martínez]] ([[Usuario discusión:Ignacio Peralta Martínez|discusión]]) 19:02 6 nov 2012 (UTC) | |||
---- | ---- | ||
Revisión actual - 12:18 1 may 2023
La topología del plano complejo
1.13 Demuestre que las raíces n-ésimas de z=1 (diferentes de 1) satisfacen la ecuación ciclotómica:
Demostración
Sea , se observa que: entonces:
por lo que las raíces de la ecuación ciclotómica son las mismas que las de la ecuación
De la última ecuación se observa que , luego , es decir, , con
Por lo tanto, las n-ésimas raices de , diferentes de 1, satisfacen la ecuación ciclotómica.
Realizado por: Pérez Córdoba Sabino (discusión) 12:43 4 dic 2012 (CST)
1.16.- Demuestre que un semi plano abierto es un conjunto abierto.
Demostración
Tenemos del cual . Decimos que . Elegimos un
(contradicción) (contradicción) .
Realizado por: Jean Carlo Cruz Venegas (discusión) 08:20 29 nov 2012 (CST)
1.19 Sea . Demuestre que:
(a) es abierto si y sólo si .
(b) es cerrado si y sólo si .
Inciso a
(a) Si es abierto, entonces para cada z ∈ existe un tal que . Vemos que la unión de todas las bolas es . Además, esta unión es igual al interior de a saber, , puesto que para cualquier subconjunto abierto de se tiene que $ A \subset \bigcup \left \{ B(x,\epsilon) : x ∈ A \right \} $ Luego .
Por otro lado, si , entonces es abierto por que es abierto.
Inciso b
(b) Si es cerrado, entonces , por que es el super conjunto cerrado más pequeño de .
Por otra parte, si entonces es cerrado debido a que es cerrado por definición.
Realizado por: Belen (discusión) 21:11 30 oct 2012 (UTC)
1.20 Sea . Demuestre que:
(a) .
(b) .
(c) $ ∂ \Omega = \Omega^{-} - \Omega ^{0} $.
(d) $ ∂ \Omega = \Omega^{-} \bigcap ( \mathbb{C} - \Omega ) ^{-} $.
Inciso a
(a)
- P.D.
Sabemos que
Entonces y es abierto, puesto que la cerradura es un conjunto cerrado y el complemento de un conjunto cerrado es abierto.
De manera que , pues el interior de un conjunto () es el mayor abierto contenido en ese conjunto ()
- P.D.
Sea $x \in (\mathbb{C} - \Omega )^{-}$, entonces $x \in \mathbb{C} - \Omega$ por que $\mathbb{C} - \Omega \subseteq ( \mathbb{C} - \Omega )^{-}$.
Como $ x ∈ \mathbb{C} - \Omega $, se tiene que $ x ∉ \Omega $ y también que $ x ∉ \Omega ^{0}$ ya que $\Omega ^{0} \subseteq \Omega $.
Puesto que $x \notin \Omega^{0} \Rightarrow x \in \mathbb{C} - \Omega ^{0}$, es decir, al complemento del interior de $\Omega$.
Tenemos entonces que , de donde .
- Ya que y , podemos decir que .
Inciso b
(b)
Sabemos que .
Ahora, del inciso anterior, , si . Sea ,
entonces: .
Y así .
Inciso c
(c)
Tenemos que .
(puesto que )
y
y (por el inciso anterior)
.
Inciso d
(d)
Veamos a la frontera como el conjunto de puntos que NO están en el interior ni en el exterior (la unión de todos los abiertos ajenos con , es decir, la unión de todos los abiertos contenidos en ). El exterior de es el interior de , o sea el conjunto .
Así,
Sabemos del inciso (a) que y del inciso (b) que .
De tal forma que .
Realizado por: Belen (discusión) 02:37 31 oct 2012 (UTC)
1.21 Sea . Demuestre que:
Inciso a
(a) si y sólo si existe tal que .
Si entonces existe un tal que , por que es abierto. Como , resulta que . En la otra dirección, si para algún , entonces por ser un conjunto abierto, se tiene que , por que es la unión de todos los subconjuntos abiertos de
Inciso b
(b) si y sólo si para todo se tiene que
Supóngase que , por 1.20 (b) y de este modo . Con esto y por el inciso anterior, se obtiene que para cada , . De esta forma, para cada hay un punto que no pertenece a , con lo cual , y así . Ahora supóngase que , entonces , y por el inciso anterior existe un tal que . De esto se obtiene que .
Realizado por: Ricardo velasco bazán (discusión) 02:41 6 nov 2012 (UTC)
1.22 Sea cualquier conjunto muestre que:
Ejercicio 1
Inciso a
es abierto relativo en .
Puesto que dice que puede ser cualquier conjunto, lo escogemos abierto, entonces será abierto relativo tal que exista un , tal que
Dado que contiene a , entonces cumple con la primera parte del parrafo 1 del texto en la pagina 17.
Inciso b
Si ,....., son abiertos relativos, es abierto relativo.
Veamos, por el inciso, hemos dicho que , tal que , esto quiere decir que podemos tomar , tal que , por lo cual se sigue cumpliendo que esa intersección de conjuntos abiertos generan a un abierto relativo.
Inciso c
Si es cualquier familia de subconjuntos de que son abiertos relativos, entonces también es abierto relativo.
Hemos mostrado en que , y es abierto relativo por , ahora tenemos , tal que por ser abiertos y su unión es , lo cual sigue generando a nuestro abierto relativo.
Ejercicio 2
Inciso a
es cerrados relativo en .
Puesto que dice que puede ser cualquier conjunto, lo escogemos cerrado, entonces será cerrado relativo tal que exista un , tal que
Inciso b
Si ,....., son cerrados relativos, es cerrado relativo.
Entonces, por el inciso, hemos dicho que , tal que , esto quiere decir que podemos tomar , tal que , por lo cual se sigue cumpliendo que esa unión de conjuntos cerrados generan a un cerrado relativo.
Inciso c
Si es cualquier familia de subconjuntos de que son cerrados relativos, entonces también es cerrado relativo.
Hemos mostrado en que , y es cerrado relativo por , ahora tenemos , tal que por ser cerrados y su unión es , lo cual sigue generando a nuestro cerrado relativo.
Realizado por: Luis Antonio (discusión) 16:39 5 dic 2012 (CST)
1.23 Si es abierto relativo, demuestre que es cerrado relativo. Demuestre también que si es cerrado relativo, entonces es abierto relativo
* Se dice que un subconjunto abierto es abierto relativo en si existe un conjunto abierto tal que .
* Se dice que un subconjunto cerrado es cerrado relativo en si existe un conjunto cerrado tal que .
Lo anterior es por el ejercicio 1.22
Podemos imaginar el analisis como el conjunto es abierto relativo, su será cerrado relativo, esto por que podrá tocar sus puntos frontera. De manera similar si es cerrado relativo, por entonces sus complemento , será abierto relativo por que no podrá tocar su frontera.
Entonces se concluye lo que nos pide demostrar el enunciado enuciado.
Realizado por: Luis Antonio (discusión) 18:08 5 dic 2012 (CST)
1.24 Demuestre que es conexo si y sólo si es un intervalo.
Sea , y sea un subconjunto abierto de tal que y (como , no es abierto en , pero si en , es decir, es abierto relativo a ). Si se prueba que no es también cerrado, entonces se habrá probado que es conexo.
Puesto que es abierto, existe un tal que . Sea el mayor para el cual , es decir . De este modo se tiene que , pero , por que de lo contrario, puesto que es abierto, habría un tal que , contradiciendo la definición de . Luego , y por tanto . Si es también cerrado, entonces es abierto, y por tanto se puede encontrar un tal que , lo cual contradice el hecho de que . Por lo tanto, no puede ser cerrado.
Ahora supóngase que no es un intervalo, entonces existen dos puntos , tal que (un teorema afirma que es un intervalo si y sólo si para cualquier par de puntos , con se tiene que ). Entonces, existe un punto tal que . Como y se tiene que , donde y son conjuntos disjuntos no vacíos. Por lo tanto, no es conexo.
Realizado por: Ricardo velasco bazán (discusión) 03:18 6 nov 2012 (UTC)
1.25 Un subconjunto se dice que es convexo si para cualquiera dos puntos se tiene que el segmento .
- (1) Demuestre que cualquier disco abierto o cerrado es convexo.
- (2) Demuestre que cualquier semiplano abierto o cerrado es convexo.
- (3) Demuestre que la intersección de cualquier familia de subconjuntos convexos es convexa.
- Demostración
Inciso 1
(1) Por definición {}
Sean , entonces ;.......................(*)
Sea arbitrario, pero fijo definido por , así todo punto del segmento [z,w] esta representado por .
- Por otra parte
al sumar y restar se tiene que agrupando y factorizando
aplicando la desigualdad del triángiulo
n Como , entonces y de las propiedades del valor absoluto tenemos que aplicando (*)
por lo que Como fue arbitrario, entonces
Así, hemos dado dos elementos cuyo segmento
Por lo tanto, un disco abierto es convexo
Para un disco cerrado solo se reemplazan la desigualdad estricta de (*) por una desigualdad.
Sean con un semiplano abierto generado por , luego & (**)
Sea arbitrario, entonces
Como y de (**) se tiene que , como fue arbitrario, entonces
Por lo tanto un semiplano abierto es convexo.
Para el caso del semiplano cerrado basta con cambiar la condición (**).
Realizado por: Pérez Córdoba Sabino (discusión) 19:17 22 nov 2012 (CST)
1.27 Si es abierto, demuestre que sus componentes conexas son abiertas también.
Tomemos una componente y un punto , como y es abierto, existe un disco . Recordando que un subconjunto no vacío, se puede descomponer como la unión de subconjuntos conexos (proposición 1.8),tenemos que la unión es conexa; y por el hecho de que un conjunto se puede llenar por subconjuntos y los intersticios que hay entre ellos se llenan con conjuntos más pequeños, debe ser igual a . Con esto se entiende que y por tanto es abierto.
Realizado por: Ignacio Peralta Martínez (discusión) 19:02 6 nov 2012 (UTC)
FUENTES (INFORMACIÓN ADICIONAL):







![u=\displaystyle{\sqrt[n]{1}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0bee50a989c38da767fcb71ac5d4a36ef6c49389)








































![\Omega^{-} = [\mathbb{C} - ( \mathbb {C} - \Omega ) ] ^{-}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1279895ddb03c3e8fd235b12c6208ec2a41b1a5c)



![[\mathbb{C} - ( \mathbb {C} - \Omega ) ] ^{-} = \mathbb{C} - (\mathbb{C} - \Omega) ^{0}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/bca850d56921e316fdcba71f427639eb39c41eec)
![{\displaystyle x\in \partial \ \Omega \Leftrightarrow x\in [\Omega \cap (\mathbb {C} -\Omega )]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/76ae3ce4b398ed95d69339ad8a798ed44480246c)
![{\displaystyle \Leftrightarrow x\in [\Omega ^{-}\cap (\mathbb {C} -\Omega )^{-}]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/e2cef5bbc36fab63d7a686b1c799f1ea308e4253)








![{\displaystyle \partial \Omega =\mathbb {C} -[\Omega ^{0}\cup (\mathbb {C} -\Omega )^{0}]=\mathbb {C} -\Omega ^{0}\cap \mathbb {C} -(\mathbb {C} -\Omega )^{0}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/47dcdffb8bac183f8331f40a8e72dc0370defd7c)



























































![I = [a,b], a,b \in \mathbb{R}, a < b](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4dc586451814d452d6c25abaa0f7fa1cb02ecf17)




























![[z,w]\subseteq](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/c73b89b4ecbfcc4b203eb0a2ce0d46f6faa3f33c)
![[z,w]:=](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/23f29c30fc0263283349c24de1046c77c2574852)

















![[z,w]\subseteq B(x,r)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8f6e41e92495b3e8eaa7f8ff01b9e6149794d272)

![[z,w]\in B(x,r)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4d01317c96326be3cacab1a4dca89f1a6dffebf7)





![z_t\in[x,y]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/eb290cc604cfe09c6b9c7d64746eb13cff635cbc)














