SECCION 1.3.1
1. Sea  . ¿Cuál es la imagen de A bajo la exponencial?.
. ¿Cuál es la imagen de A bajo la exponencial?.
La imagen de la recta horizontal  bajo esta función
bajo esta función
es la semilinea que surge del origen con argumento  ,
,
entonces lo que pasa por el punto

De igual forma para 

Por otra parte tenemos  , entonces la linea vertical
, entonces la linea vertical 
se transforma en el circulo de radio

De igual forma para  , se transforma en el circulo de radio
, se transforma en el circulo de radio

--Ralf Gutierrez 03:11 22 nov 2009 (UTC)
2.- Exprese  , en la forma
, en la forma  .
.
por propiedades de la exponencial sabemos que:

y que 
entonces la exprecion completa seria:


 .
.
--Josua Da Vinci 18:19 17 nov 2009 (UTC)
3.- Demuestre que la funcion exponencial compleja no está acotada en ninguna semirrecta por el origen. Describa la imagen.
Para realizar esta demostracion tomamos la función exponencial compleja de la siguiente manera:
![\exp\left[iy\right]=\lim_{n\to\infty}\left(1+\frac{iy}{n}\right)^{n}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/dce42377d9f468b21a893bd715db24fe3066bd4f)
Recordando que la exponencial se puede escribir de la siguiente manera

Ahora tomando la norma al cuadrado en ambos lados

Despejando  y elevando a la
y elevando a la  , tenemos la siguiente expresion:
, tenemos la siguiente expresion:

Tomando el 

Hacemos el cambio de variable  y tomamos el limite
y tomamos el limite


Para  tenemos que
tenemos que  ,
haciendo
,
haciendo  ,
,  .
.

![\exp\left[iy\right]=\lim_{n\rightarrow\infty}\left(1+\frac{iy}{n}\right)^{n}=\cos y+i\sin y](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f4ec12b9f230754910f73845f7fae3430dfe1205) .
.
Con esto queda demostrado que la exponencial compleja no está acotada
por ninguna semirrecta.
La imagen se transforman en un rayo con ángulo  , que parte del
origen y que va creciendo conforme crece la
, que parte del
origen y que va creciendo conforme crece la  .
.
--Oscar Adrian 04:19 2 dic 2009 (UTC)
4.-Demuestre que bajo la accion de la función exponencial, dos líneas horizontales, símetricas con respecto al eje  , se transforman en dos semirrectas por el origen que son conjugadas una de otra.
, se transforman en dos semirrectas por el origen que son conjugadas una de otra.
Solución.
Basta con demostrar que

Sea

Si tomamos el conjugado de la última expresión tenemos que:



Debemos tener en cuenta que  es un punto y que para tener una recta o un segmento de ella debemos incluir
es un punto y que para tener una recta o un segmento de ella debemos incluir  .
.
--Dali 04:12 15 nov 2009 (UTC)
5 ¿Que puntos del plano complejo cumplen  ?
?
Solución:
Sea  y
y 
Entonces


(Recordemos que:  y
y 
Por lo tanto

--Dali 07:12 7 dic 2009 (UTC)
SECCION 1.3.2
2 Calcule todos los valores que toman las distintas ramas del logaritmo de  .
.
Solución.
Expresemos  en su forma polar
en su forma polar


Ahora recordemos que

Si tomamos los valores encontrados para  y
y  la ultima expresion toma la forma
la ultima expresion toma la forma

De donde el valor principal se obtiene haciendo  .
.
--Dali 07:21 7 dic 2009 (UTC)
SECCION 1.3.3
1.Calcule todos los valores 


recordando
 ,
,  y
y 
 =
= 


sustituyendo 
 Nota: encontrando todos los posibles valores proponemos
Nota: encontrando todos los posibles valores proponemos 



donde
 y
y  valen 1
valen 1  los valores encontrados seran multiplos de
los valores encontrados seran multiplos de 

 donde k pertenece a los numeros naturales.
donde k pertenece a los numeros naturales.
ahora encontrando los valores 
 donde
donde  Nota: encontrando todos los posibles valores proponemos
Nota: encontrando todos los posibles valores proponemos 

 para cualquier w
para cualquier w
finalmente calculando los valores 


 para cualquier z
para cualquier z
--Karla 19:18 7 nov 2009 (UTC)Karla.
3.- Demuestre que si  , entonces
, entonces  .
.
Solución.
Sea 
Entonces

pues

como

si tomamos el cambio  obtenemos que
obtenemos que

Pues  .
.
--Dali 02:23 15 nov 2009 (UTC)
4. Exhiba  para las cuales no se cumpla
para las cuales no se cumpla  .
.
Sean  de la forma
de la forma 

como  se cumple
se cumple 
desarrollamos: 




Esta igualdad se cumple para  con
con 
por lo tanto  no se cumple para
no se cumple para  con
con  --Gabita 20:22 12 nov 2009 (UTC)
--Gabita 20:22 12 nov 2009 (UTC)
SECCION 1.3.4
1. Pruebe la identidad  .
.
Sabemos que


Entonces



--Ralf Gutierrez 19:16 10 nov 2009 (UTC)
2. Pruebe que el minimo periodo de las funciones  y
y  es
es  .
.



y  para
para  con
con 

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle sen{z + 2\pi} = sen{z + 2\pin}}
con 
entonces el minimo periodo de  es
es  .
.



y  para
para  con
con 
Error al representar (función desconocida «\pin»): {\displaystyle cos{z} = cos{z + 0} = cos{z + 2\pi} = sen{z + 2\pin}}
con 
entonces el minimo periodo de  es
es  .
.
3. Pruebe el tercer inciso de la Proposición 1.3.9.
Dadas  , se cumple la siguiente igualdad
, se cumple la siguiente igualdad
 .
.
Sabemos que


Entonces

![=\frac{1}{4}\left [e^{i(z+w)}+e^{-i(z+w)}+e^{i(z-w)}+e^{-i(z-w)}\right ]+\frac{1}{4}\left [e^{i(z+w)}+e^{-i(z+w)}-e^{i(z-w)}-e^{-i(z-w)}\right ]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0c47f8a288526a5e21d6f20ac1a72c9a659a64fa)
![=\frac{1}{2}\left [e^{i(z+w)}+e^{-i(z+w)}\right ]=cos(z+w)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/05abccbbe9c58ad657889e8ada094dfcff7902b2)


--Ralf Gutierrez 19:18 10 nov 2009 (UTC)
4.- Resuelva  ,
,  y
y  .
.
Sabemos que

Y queremos reolver

Entonces igualando estas dos ecuaciones tenemos lo siguiente:

Haciendo un poco de algebra que a continuación se muestra, despejamos  , que es el valor del numero que queremos encontrar
, que es el valor del numero que queremos encontrar

Multiplicando lo anterior por 

Que esta ya es facil de resolver a partir de

Entonces tetenemos que

Y tomando el logaritmo en ambos lados


 para
para  , tenemos que
, tenemos que

Y para


Ahora haciendo el mismo procedimiento para  , tenemos que
, tenemos que

 para
para  , tenemos que
, tenemos que

--Oscar Adrian 06:05 4 dic 2009 (UTC)
5. Demuestre la identidad 
partiendo de que puedo expresar:

y
 .
.
entonces en terminos de las exponenciales obtengo.
 .
.
resolviendo el producto y simplificando, obtengo:


--Josua Da Vinci 18:08 1 dic 2009 (UTC)
KARLA: yo hago los dos ejercicios que faltan en esta sección, creo que son el 2 y 4, es asi? atte. Gaby Durán
por cierto no he asistido a clase por problemas familiares, pero estoy trabajando.
--Karla 19:21 7 nov 2009 (UTC)Karla
9.- Describa la geometría de  en la región
en la región  .
Sugerencia: Usar (1.8).
.
Sugerencia: Usar (1.8).
Para describir la geometría de esta función tomamos la siguiente igualdad

Que esto nos dice que nuestra nueva grafica sera la del seno pero desfasada 
Asi mismo tomando como referencia la figura 1.23 de la pagina 44 del
libro de texto nuestro resultado geometrico es el siguiente:
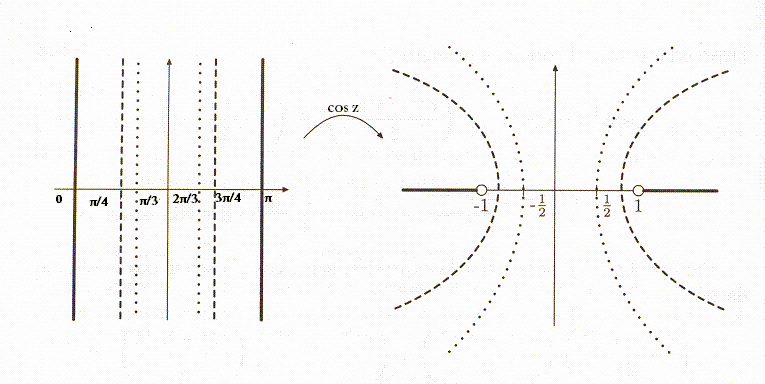
--Oscar Adrian 05:09 2 dic 2009 (UTC)
Compleja:ej-cap1.1
Compleja:ej-cap1.2
Compleja:ej-cap1.4


















![\exp\left[iy\right]=\lim_{n\to\infty}\left(1+\frac{iy}{n}\right)^{n}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/dce42377d9f468b21a893bd715db24fe3066bd4f)














![\exp\left[iy\right]=\lim_{n\rightarrow\infty}\left(1+\frac{iy}{n}\right)^{n}=\cos y+i\sin y](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/f4ec12b9f230754910f73845f7fae3430dfe1205)


































































































![=\frac{1}{4}\left [e^{i(z+w)}+e^{-i(z+w)}+e^{i(z-w)}+e^{-i(z-w)}\right ]+\frac{1}{4}\left [e^{i(z+w)}+e^{-i(z+w)}-e^{i(z-w)}-e^{-i(z-w)}\right ]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/0c47f8a288526a5e21d6f20ac1a72c9a659a64fa)
![=\frac{1}{2}\left [e^{i(z+w)}+e^{-i(z+w)}\right ]=cos(z+w)](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/05abccbbe9c58ad657889e8ada094dfcff7902b2)































