EJERCICIOS 1.2.1
1. Demuestre que una una funcion  es continua en
es continua en  si y soló si para toda sucesión
si y soló si para toda sucesión  tal que
tal que  cuando
cuando  se tiene
se tiene  cuando
cuando 
DEMO:
Supongamos que  es continua en
es continua en  , es decir:
, es decir:
$\forall \epsilon > 0,\quad\exists \delta = \delta(\epsilon)> 0 $
tal que 
y supongamos que  es una sucesión en
es una sucesión en  tal que
tal que 
P.D.


como  es continua en
es continua en 





--Luis Antelmo 23:52 10 oct 2009 (UTC)
2. Demuestre que una sucesión  en
en  es de Cauchy si y sólo es convergente.
es de Cauchy si y sólo es convergente.
DEMO:
Una sucesión en  se dice que es de Cauchy si para todo
se dice que es de Cauchy si para todo  tal que
tal que  .
.
P.D.
Si la sucesión es convergente, esto es si 
tal que 
 si
si  se tiene que
se tiene que


--Luis Antelmo 23:52 10 oct 2009 (UTC)
EJERCICIOS 1.2.2
REVISADO
1. Demuestre que la funcion estereográfica  de la esfera de Riemann en el plano complejo extendido es suprayectiva.
de la esfera de Riemann en el plano complejo extendido es suprayectiva.
Definicion: Una funcion es suprayectiva si a un punto en la esfera le corresponde uno(s) puntos dentro del plano complejo
le corresponde uno(s) puntos dentro del plano complejo 
Una función es sobre si para toda y pertenece al Codominio  ,existe x pertenece al Dominio de
,existe x pertenece al Dominio de
 tal que
tal que 
Notaciòn (para la demostraciòn): S= Esfera, C= punto en el plano proyectado por la esfera.
Dominio y el Codominio
y el Codominio y tambièn
y tambièn


Suponga  S donde
S donde 
Condicion de la esfera  donde
donde  pertenece a i
pertenece a i
Ahora bien sabemos que la magnitud cuadrática  es 1
es 1
 Codominio de (f)
Codominio de (f)
Sea y que pertenece al Codominio de (f) donde : 
Sea  y
y 
tomando en cuenta que 
de esta manera 
--Karla 03:09 21 oct 2009 (UTC)Sanchez
REVISADO
2. Demuestre que si  cuando
cuando  , entonces
, entonces  cuando
cuando 
Como 

Recordando la definiciòn del limite dado un  nos aproximamos.
nos aproximamos.
 por hipótesis.
por hipótesis.
P.D.  , asi como también
, asi como también 
Ahora usando la definiciòn del limite dentro de la mètrica cordal tenemos un  donde limite se aproxima a cero cuando
donde limite se aproxima a cero cuando 
P.D.
P.D.
Usando la definición de la distancia cordal entre dos puntos

P.D.
Tomamos el lìmite descrito anteriomente.
Por hipótesis  tal que
tal que 
Sea  como antes por la continuidad de
como antes por la continuidad de 
Finalmente usando la definiciòn de metrica cordal.
Si 
--Karla 04:20 21 oct 2009 (UTC)Sanchez
3. Las transformaciones de Möbius definidas en (1.4) se extienden a la esfera de Riemann  como sigue: si
como sigue: si  , y si
, y si  y
y  .Demuestre que estas funciones son continuas en dicha esfera con la metrica cordal.
.Demuestre que estas funciones son continuas en dicha esfera con la metrica cordal.
Transformaciones de Möbius complejas.(1.4)

Se define la metrica cordal en el plano complejo extendido de la sig. manera.


para los casos extremos.
si 
si 
si 
generalizando, para  , (arbitrarias).
, (arbitrarias).
por hip.
 .
.

tal que si
 .
.
entonces
 .
.

por 

ahora si y
y  donde
donde 
con la metrica cordal.



ya q se mostro que 
es continua, se puede probar lo mismo para
 .
.
por teo. de continuidad si

son continuas, tambien
 , es continua.
, es continua.

es continua si

--Josua Da Vinci 00:42 21 oct 2009 (UTC)
4.Demuestre que si AB son matrices que representan (de la manera obvia) dos transformaciones de Möbius f,g, respectivamente, entonces la matriz BA representa la composicion gf, que también es de Möbius.Concluya mostrando que estas transformaciones son funciones bicontinuas de la esfera en sí misma, y que ademas constituyen un grupo.
SOLUCION:
tenemos que  son transformaciones de Möbius
son transformaciones de Möbius

sean  las representaciones matriciales de
las representaciones matriciales de  respectivamente
respectivamente

entonces

entonces

los elementos de la matriz BA son elementos de funciones biyectivas, entonces dicha matriz también es biyectiva, y por lo tanto gf es biyectiva y de Möbius.
Por ser de Möbius es meromorfa, ahora notemos que gf es continua y que

tambien es continua por lo que concluimos que es bicontinua.
--Wendy 04:26 18 oct 2009 (UTC)
5.Demuestre que las transformaciones de Möbius son transitivas en ternas de puntos de la esfera de Riemann. Sugerencia: Dada una terna, encuentre una función de Möbius que la mande en 1, 0 e 
Sea 
Sea 
con 
y  ;
; 
entonces 

Sea 
con 


Sea 
con 
entonces 
6.Pruebe que las transformaciones de Möbius son composición de algunas de las siguientes funciones: rotaciones, traslaciones, homotecias, y  . Concluya mostrando que las transformaciones de Möbius preservan la familia de circulos y rectas.
. Concluya mostrando que las transformaciones de Möbius preservan la familia de circulos y rectas.
Considere la Transformación de Möbius.

Sea  se tiene:
se tiene:
 entonces
entonces  es una traslación.
es una traslación.
Sea  se tiene:
se tiene:
 entonces T(z) es una rotación por arg(a) y por una amplificación
entonces T(z) es una rotación por arg(a) y por una amplificación  .
.
Sea  se tiene:
se tiene:
 entonces T(z) es una inversión.
entonces T(z) es una inversión.
Las transformaciones de MÖebius preservan la familia de circulos y rectas:
Las traslaciones, homotecias y rotaciones transforman lineas en lineas y circulos en circulos, vamos a verificar si las inversiones preservan la familia de circulos y rectas.
Una linea o un circulo esta determinado por la ecuacion 1:
 ...(1)
...(1)
Sea  con
con 
y sea 



de modo que


Reacomodamos la ecuacion 1
![\Big ( \frac{1}{x^2 + y^2}\Big )\Big [A x + B y + C (x^2 + y^2)\Big ] = D \Big ( \frac{1}{x^2 + y^2}\Big )](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/53c4c390072d1286e8ab62af99266b947d7eaabe)



que tambien es un circulo o una recta.
--Gabita 23:28 26 nov 2009 (UTC)
7. Demuestre que las transformaciones de Möbius son transitivas en la familia de círculos y rectas.
Puesto que una transformación del tipo  aplica en circunferencias y rectas, y como las rotaciones, los cambios de escala y las translaciones preservan rectas y circunferencias. Dicha transformación bilineal o de Möbius aplica en círculos y rectas.
aplica en circunferencias y rectas, y como las rotaciones, los cambios de escala y las translaciones preservan rectas y circunferencias. Dicha transformación bilineal o de Möbius aplica en círculos y rectas.
Un círculo en  es la intersección de un plano con la esfera, por lo cual satiface la siguiente ecuación:
es la intersección de un plano con la esfera, por lo cual satiface la siguiente ecuación:

Tenemos que



Por lo tanto, este círculo es la imagen bajo la proyección esterografica, cuyos puntos satisfacen la siguiente ecuación en el plano:

Escribiendo  , se tiene
, se tiene





finalmente se tiene que
 ,
,
que biene siendo la ecuación de una recta o un círculo, dependiendo si  , o si
, o si  .
.
7. Demuestre que las transformaciones de Möbius son transitivas en la familia de círculos y rectas.
Puesto que una transformación del tipo  aplica en circunferencias y rectas, y como las rotaciones, los cambios de escala y las translaciones preservan rectas y circunferencias. Dicha transformación bilineal o de Möbius aplica en círculos y rectas.
aplica en circunferencias y rectas, y como las rotaciones, los cambios de escala y las translaciones preservan rectas y circunferencias. Dicha transformación bilineal o de Möbius aplica en círculos y rectas.
Puesto que 


Por tanto, la imagen de  es
es
 .
.
Sabemos que el lugar geométrico de toda sección cónica viene dado por

Esta ecuación representa una sircunferencia si  y
y 
Entonces

representa una recta si  y una circunferencia si
y una circunferencia si  . Su imagen es
. Su imagen es

o
 .
.
--Ralf Gutierrez 16:08 22 oct 2009 (UTC)
8.- Demuestre de dos maneras que el lugar de los puntos que cumplen la ecuación 
 constituye una recta o un círculo (llamado de Apolonio).
constituye una recta o un círculo (llamado de Apolonio).
Solución
Sea

Entonces





Si agrupamos esta expresión se tiene:

Si  se tiene la ecuación de una recta, es decir:
se tiene la ecuación de una recta, es decir:

Ahora para  la ecuación
la ecuación  al multiplicarla por
al multiplicarla por
 toma la forma:
toma la forma:

Si completamos los cuadrados (más un poco de álgebra) de esta ultima expresión se obtiene lo
siguiente


lo cual es la ecuación de un círculo con centro
 y cuyo radio es
y cuyo radio es
 .
.
Otro método.



agrupando tenemos


si tomamos el cambio , la anterior ecuación se escribe como
, la anterior ecuación se escribe como

si  (entonces
(entonces  ) se tiene la ecución de una recta, si
) se tiene la ecución de una recta, si  es distinto
de cero (entonces k es distinto de 1) y se tiene la ecuación de una
circunferencia.
es distinto
de cero (entonces k es distinto de 1) y se tiene la ecuación de una
circunferencia.
--Dali 01:46 15 nov 2009 (UTC)
9.- Sean  complejos, tal que no son ambos nulos, probar que
complejos, tal que no son ambos nulos, probar que
 , si
, si  .
Interpretar geometricamente.
.
Interpretar geometricamente.
Sean  .
Entonces sustituyendo esto se tiene la siguiente expresión:
.
Entonces sustituyendo esto se tiene la siguiente expresión:

Por propiedades de la norma se sigue que

Y multiplicando ambos lados por el denominador llegamos a que

Desarrollando los producto y las operaciones para poder agrupar terminos se llega a

Elevando al cuadrado para tener el cuadrado de la norma tenemos que

Donde es inmediato lo siguiente

Y despues de expander los polinomios


Donde 

O tambien

Que era lo que se queria mostrar.
Ahora geometricamente esto nos dice que la magnitud de la suma de
dos numeros complejos es igual a la magnitud de la suma de sus conjugados.
En las siguientes imagenes se muestra graficamente la interpretacion
geometrica, el vector de color naranja es  y el azul y verde
y el azul y verde  respectivamente.
respectivamente.
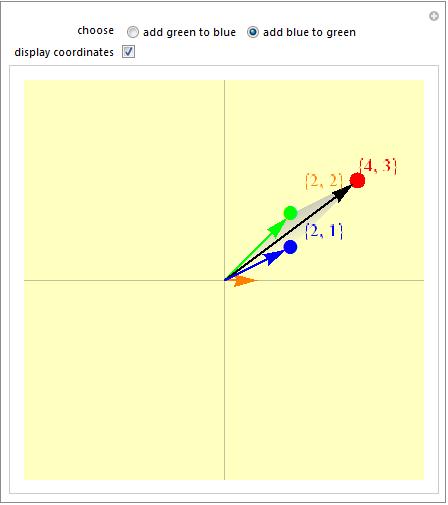
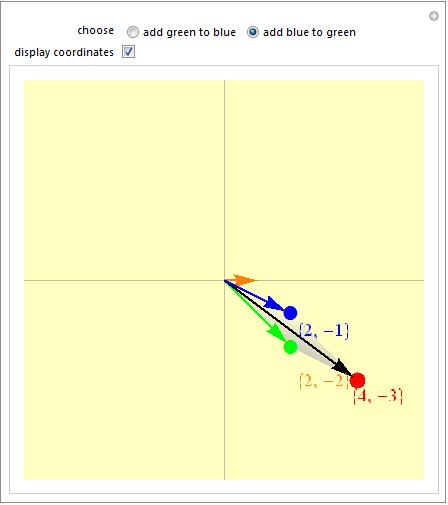
--Oscar Adrian 14:12 9 dic 2009 (UTC)
--Oscar Adrian 19:42 21 nov 2009 (UTC)
10.- Probar que la funcion  es una rotacion de
es una rotacion de  radianes en la esfera de Riemann alrededor del eje x.
radianes en la esfera de Riemann alrededor del eje x.
Las componentes del punto  en la esfera unitaria asociado a z son:
en la esfera unitaria asociado a z son:

Sea  y tomando en cuenta que
y tomando en cuenta que  , entonces, las componentes del punto
, entonces, las componentes del punto  de la esfera unitaria asociado a
de la esfera unitaria asociado a  son:
son:


 ...
...
--Luis Nava 00:03 9 nov 2009 (UTC)
11. Probar que dados dos puntos  se tiene que sus proyecciones en la esfera de Riemann son antípodas si y solo si
se tiene que sus proyecciones en la esfera de Riemann son antípodas si y solo si 
SOLUCION.
Sea 
se pasa del plano complejo a la esfera de Riemann.


Si  es el punto P en la esfera de Riemann.
es el punto P en la esfera de Riemann.
con este punto P y el centro C de la esfera se construye una recta que pase por estos puntos:
Sea  donde
donde  es el vector director que va de P a C esto es
es el vector director que va de P a C esto es

nuestra ecuacion de la recta queda de la siguiente manera:

Cuando  tenemos a
tenemos a  en la esfera.
en la esfera.
cuando  tenemos el centro
tenemos el centro  de la esfera de Riemann.
de la esfera de Riemann.
cuando  tenemos al punto
tenemos al punto  que es la antipoda de
que es la antipoda de 

teniendo a  sobre la esfera de Riemann volvemos al plano complejo mediante la siguiente tranformacion:
sobre la esfera de Riemann volvemos al plano complejo mediante la siguiente tranformacion:

 , que nos da un punto
, que nos da un punto 


Como la proyeccion en la esfera de Riemann de  es la antipoda de
es la antipoda de  se debe de cumplir que
se debe de cumplir que 
Sea 


 son antipodas si y solo si
son antipodas si y solo si 
--Luis Antelmo 15:11 21 oct 2009 (UTC)
12.¿Cuál es la imagen de una recta por el origen bajo la funcion  ?
?
SOLUCIÓN:
para la imagen notemos que  es continua exepto cuando
es continua exepto cuando  , por lo que su imagen es todo el plano complejo exepto el origen.
, por lo que su imagen es todo el plano complejo exepto el origen.
--Wendy 04:26 18 oct 2009 (UTC)
Compleja:ej-cap1.1
Compleja:ej-cap1.2
Compleja:ej-cap1.3
Compleja:ej-cap1.4
Compleja:ej-cap2.1
Compleja:ej-cap2.2
Compleja:ej-cap2.3
Compleja:ej-cap2.4
Compleja:ej-cap2.5
Compleja:ej-cap3.1
Compleja:ej-cap3.2
Compleja:ej-cap3.3
Compleja:ej-cap3.4
Compleja:ej-cap1.1




































































































































![\Big ( \frac{1}{x^2 + y^2}\Big )\Big [A x + B y + C (x^2 + y^2)\Big ] = D \Big ( \frac{1}{x^2 + y^2}\Big )](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/53c4c390072d1286e8ab62af99266b947d7eaabe)




















































































































