Compleja:ej-cap1.1.3

SECCION 1.1.3

1. Calcule las raíces cuadradas de $3+4i$ y de $1+2i$.

Aplicando la formula para calcular raíces cuadradas de números complejos.

$\pm \left({\sqrt {\frac {a+{\sqrt {a^{2}+b^{2}}}}{2}}}+i{\sqrt {\frac {-a+{\sqrt {a^{2}+b^{2}}}}{2}}}\right)$ si $\quad b>0$

Por lo tanto las raices de $3+4i$, son:

$=\pm \left({\sqrt {\frac {3+{\sqrt {25}}}{2}}}+i{\sqrt {\frac {-3+{\sqrt {25}}}{2}}}\right)$

$=\pm \left({\sqrt {\frac {8}{2}}}+i{\sqrt {1}}\right)$

$=\pm \left(2+i\right)$

y para $1+2i$, son:

$=\pm \left({\sqrt {\frac {1+{\sqrt {5}}}{2}}}+i{\sqrt {\frac {-1+{\sqrt {5}}}{2}}}\right)$

$=\pm \left({\sqrt {1.61}}+i{\sqrt {0.61}}\right)$

$=\pm \left(1.27+i0.78\right).$

---

Realizado por: Josua Da Vinci 23:44 30 sep 2009 (UTC)

---

REVISADO

2.- Calcule las raíces sextas de -64 y las raíces cubicas de 8i

Tenemos que $cos{\boldsymbol {\theta }}+isen{\boldsymbol {\theta }}=-64$ definicion en forma polar

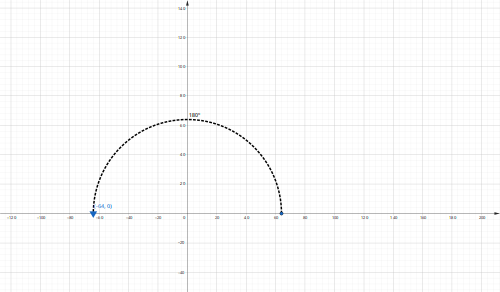
r=64

n=6 porque nos piden las raíces sextas

Entonces el argumento ${\boldsymbol {\theta }}=\pi$

Si $x+iy=re^{i{\boldsymbol {\theta }}}$

Entonces utilizando la Fórmula de Moivre para obtener las raíces

$(ge^{i{\boldsymbol {\phi }}n})=re^{i{\boldsymbol {\theta }}}$

Ahora tenemos

$g^{n}=r$ y g= raíz enesima ${\sqrt {64}}$= = 2

y ${\boldsymbol {\phi }}n={\boldsymbol {\theta }}+2k\pi$ los $2\pi$ es porque tomamos en cuenta la periodicidad de la funció n y k son todos los múltiplos de $2\pi$ entonces sacando las raíces

${\boldsymbol {\theta }}=\pi /6$ k=0

${\boldsymbol {\theta }}=\pi /6+2\pi /6=3\pi /6$ k=1

${\boldsymbol {\theta }}=\pi /6+2(2)\pi /6=5\pi /6$ k=2

${\boldsymbol {\theta }}=\pi /6+(3)2\pi /6=7\pi /6$ k=3

${\boldsymbol {\theta }}=\pi /6+2(4)\pi /6=9\pi /6$ k=4

${\boldsymbol {\theta }}=\pi /6+2(5)\pi /6=11\pi /6$ k=5

Las soluciones son

r1= 2 $e^{i(\pi /6)}$

r2= 2 $e^{i(3\pi /6)}$

r3= 2 $e^{i(5\pi /6)}$

r4= 2 $e^{i(7\pi /6)}$

r5= 2 $e^{i(9\pi /6)}$

r6= 2 $e^{i(11\pi /6)}$

Graficando en coordenadas polares nos queda:

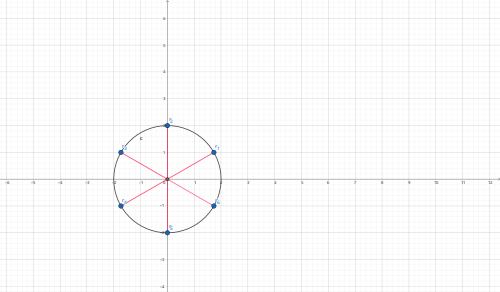
Haciendo algo similar para el 8i Tenemos

$cos{\boldsymbol {\theta }}+isen{\boldsymbol {\theta }}=8i$

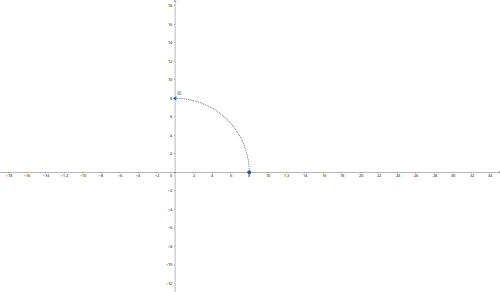
El argumento ${\boldsymbol {\theta }}=\pi /2$

r= 8

n=3 porque nos piden las raíces cubicas

$g^{n}=r$ y g= raíz enesima ${\sqrt {8}}$= = 2

${\boldsymbol {\phi }}n={\boldsymbol {\theta }}+2k\pi$

${\boldsymbol {\phi }}={\boldsymbol {\theta }}+2k\pi =\pi /6$ k=0

${\boldsymbol {\phi }}=\pi /6+2\pi /3=5\pi /6$ k=1

${\boldsymbol {\phi }}==\pi /6+2(2)\pi /3=9\pi /6$ k=2

r1= 2 $e^{i(\pi /6)}$

r2= 2 $e^{i(5\pi /6)}$

r3= 2 $e^{i(9\pi /6)}$

Gráficando en coordenadas polares tenemos

---

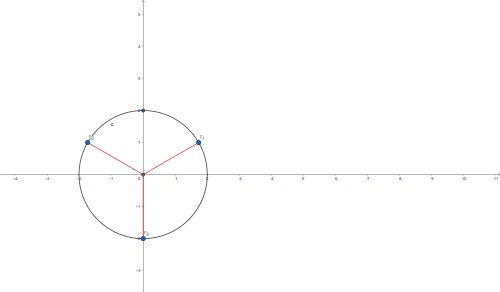
Realizado por: Karla 21:35 4 oct 2009 (UTC)Sanchez

---

2.- Calcule las raíces sextas de -64 y las raíces cubicas de 8i

Sea $z=-64=64(cos\pi +isen\pi )\,$

Por la Fórmula de Moivre

$z^{1/6}=64^{1/6}(cos\pi +sen\pi )^{1/6}=2(cos({\frac {\pi +2k\pi }{6}})+isen({\frac {\pi +2k\pi }{6}}))$ para k = 0,1,2,3,4,5

Evaluando k se obtiene

con k = 0

$w_{0}=2(cos({\frac {\pi }{6}})+isen({\frac {\pi }{6}}))={\sqrt {3}}+i$

con k = 1

$w_{1}=2(cos({\frac {\pi +2\pi }{6}})+isen({\frac {\pi +2\pi }{6}}))=2(cos({\frac {\pi }{2}})+isen({\frac {\pi }{2}}))=2i$

con k = 2

$w_{2}=2(cos({\frac {\pi +4\pi }{6}})+isen({\frac {\pi +4\pi }{6}}))=2(cos({\frac {5\pi }{6}})+isen({\frac {5\pi }{6}}))=-{\sqrt {3}}+i$

con k = 3

$w_{3}=2(cos({\frac {\pi +6\pi }{6}})+isen({\frac {\pi +6\pi }{6}}))=2(cos({\frac {7\pi }{6}})+isen({\frac {7\pi }{6}}))=-{\sqrt {3}}-i$

con k = 4

$w_{4}=2(cos({\frac {\pi +8\pi }{6}})+isen({\frac {\pi +8\pi }{6}}))=2(cos({\frac {3\pi }{2}})+isen({\frac {3\pi }{2}}))=-2i$

con k = 5

$w_{5}=2(cos({\frac {\pi +10\pi }{6}})+isen({\frac {\pi +10\pi }{6}}))=2(cos({\frac {11\pi }{6}})+isen({\frac {11\pi }{6}}))={\sqrt {3}}-i$

..............

Sea $z=8i=8(cos({\frac {\pi }{2}})+sen({\frac {\pi }{2}})\,$

$z^{1/3}=8^{1/3}(cos({\frac {\pi }{2}})+isen({\frac {\pi }{2}}))^{1/3}=2(cos({\frac {{\frac {\pi }{2}}+2k\pi }{3}})+isen({\frac {{\frac {\pi }{2}}+2k\pi }{3}}))$ para k = 0,1,2

Evaluando a k se obtiene

con k = 0

$w_{0}=2(cos({\frac {\pi }{6}})+isen({\frac {\pi }{6}})={\sqrt {3}}+i$

con k = 1

$w_{1}=2(cos({\frac {{\frac {\pi }{2}}+2\pi }{3}})+isen({\frac {{\frac {\pi }{2}}+2\pi }{3}}))=2(cos({\frac {5\pi }{6}})+isen({\frac {5\pi }{6}})=-{\sqrt {3}}+i$

con k = 2

$w_{2}=2(cos({\frac {{\frac {\pi }{2}}+4\pi }{3}})+isen({\frac {{\frac {\pi }{2}}+4\pi }{3}}))=2(cos({\frac {3\pi }{2}})+isen({\frac {3\pi }{2}}))=-2i$

---

Realizado por: Luis Nava 21:07 3 oct 2009 (UTC)

---

3. Demuestre que $\ 1+Z+Z^{2}+...+Z^{n-1}=0$ donde z es una raíz n-ésima de la unidad, $z\neq 1$

Sea $\ S=1+Z+Z^{2}+...+Z^{n-1}$

Ahora multiplicamos ambos lados por Z

$\ ZS=Z+Z^{2}+Z^{3}+...+Z^{n-1}+Z^{n}$

Restando la segunda ecuación de la primera

$\ {(s=1+z+z^{2}+...+z^{n-1})-(zs=z+^{2}+z^{3}+...+z^{n-1}+z^{n})}$

Tenemos que

$\ {s-zs=1-z^{n}}$

entonces

$\ {s(1-z)=1-z^{n}}$

De donde

$s={\frac {1-z^{n}}{1-z}}$

Como z es una raíz enesima de la unidad

$0={\frac {1-z^{n}}{1-z}}$

$\ {1-z^{n}=0}$

$\ {z^{n}=1}$

Entonces

$\ {z^{n}=1}$

y

${1-z}\neq {0}$

porque

${z}\neq {1}$

Por lo tanto

${s=0}$

---

Realizado por: Ralf Gutierrez 22:00 2 oct 2009 (UTC)

---

4. Demuestre que:

${\frac {n}{2^{n-1}}}=\prod _{k=1}^{n-1}\sin {\frac {\pi }{k}}$

Sugerencia: Factoriza la expresión $1+z+z^{2}+\cdots +z^{n}$ usando las raíces n-ésimas de la unidad, posteriormente evalue en $z=1$.

Solución:

Las raices de $z^{m}=1$ son

$z=1,e^{\frac {2\pi i}{m}},e^{\frac {4\pi i}{m}},\dots ,e^{\frac {(2m-1)\pi i}{m}}$

entonces podemos escribir

$z^{m-1}=(z-e^{\frac {2\pi i}{m}})(z-e^{\frac {4\pi i}{m}})\cdots (z-e^{\frac {(2m-1)\pi i}{m}})$

dividiendo ambos lados por $z-1$ y haciendo $z=1$:

${\frac {z^{m-1}}{z-1}}=1+z+z^{2}+\cdots +z^{m-1}$

de aqui hallamos que

$m=(1-e^{\frac {2\pi i}{m}})(1-e^{\frac {4\pi i}{m}})\cdots (1-e^{\frac {(2m-1)\pi i}{m}})\qquad (1)$

tomando el conjugado complejo de ambos lados de (1)

$m=(1-e^{\frac {-2\pi i}{m}})(1-e^{\frac {-4\pi i}{m}})\cdots (1-e^{\frac {-(2m-1)\pi i}{m}})\qquad (2)$

Multiplicando la ecuación (1) por la (2) y aplicando que

$1-(1-e^{\frac {2k\pi i}{m}})(1-e^{\frac {2k\pi i}{m}})=2-2\cos {\frac {2k\pi }{m}}$

tenemos

$m^{2}=2^{m-1}(1-\cos {\frac {2\pi }{m}})(1-\cos {\frac {4\pi }{m}})\cdots (1-\cos {\frac {2(m-1)\pi }{m}})$

puesto que

$1-\cos {\frac {2k\pi }{m}}=2\sin ^{2}{\frac {k\pi }{m}}$

la ecuación anterior se transforma en

$m^{2}=2^{2m-2}(\sin ^{2}{\frac {\pi }{m}})(\sin ^{2}{\frac {2\pi }{m}})\cdots (\sin ^{2}{\frac {(m-1)\pi }{m}})$

despejando y sacando la raíz en ambos lados de la expresión:

${\frac {m}{2^{m-1}}}=(\sin {\frac {\pi }{m}})(\sin {\frac {2\pi }{m}})\cdots (\sin {\frac {(m-1)\pi }{m}})$

lo que queda demostrada la igualdad.

---

Realizado por:Wendy 23:10 4 oct 2009 (UTC)

---

5. Demuestre que

$1+cos\phi +cos2\phi +...............+cosn\phi ={\frac {1}{2}}+{\frac {sen\left(n\phi +{\frac {\phi }{2}}\right)}{2sen\left({\frac {\phi }{2}}\right)}}$,

donde $\phi$ no es un multiplo par de $\pi$.

Esta identidad se le atribuye a Lagrange.

Sugerencia: calcular la parte real de

$1+z+z^{2}+..........+z^{n}$, donde $z=cos\phi +isen\phi$.

Solucion.

Sea

$S=1+z+z^{2}+.......+z^{n}$ si multiplicamos por $z$ a $S$ se tiene que

$zS=z+z^{2}+z^{3}+......+z^{n}+z^{n+1}$ ahora restemos estas dos ultimas expresiones

$\left(S-zS\right)=\left(1-z\right)S=1-z^{n+1}$ de lo que se obtiene que

$S={\frac {1-z^{n+1}}{1-z}}$

Si en esta última expresion utilizamos $z=cos\phi +isen\phi$ entonces

$S={\frac {1-z^{n+1}}{1-z}}$

toma la siguiente forma

$1+\left(cos\phi +isen\phi \right)+\left(cos\phi +isen\phi \right)^{2}+........+\left(cos\phi +isen\phi \right)^{n}={\frac {1-\left(cos\phi +isen\phi \right)^{n+1}}{1-\left(cos\phi +isen\phi \right)}}$

que es equivalente a esta

$1+\left(cos\phi +isen\phi \right)+\left(cos2\phi +isen2\phi \right)+........+\left(cosn\phi +isen\left(n\phi \right)\right)={\frac {1-\left(cos\left(n+1\right)\phi +isen\left(n+1\right)\phi \right)}{1-\left(cos\phi +isen\phi \right)}}$

Tomando el lado derecho de esta ultima expresión y llevar a cabo el producto con su conjugado , es decir:

$\left({\frac {1-cos\left(n\phi +\phi \right)-isen\left(n\phi +\phi \right)}{1-cos\phi -isen\phi }}\right)\star \left({\frac {1-cos\phi +isen\phi }{1-cos\phi +isen\phi }}\right)$

Se obtiene del numerador lo siguiente

$1-cos\phi +isen\phi -cosn\left(n\phi +\phi \right)+cos\phi cos\left(n\phi +\phi \right)-isen\phi cos\left(n\phi +\phi \right)-isen\left(n\phi +\phi \right)+icos\phi sen\left(n\phi +\phi \right)+sen\phi sen\left(n\phi +\phi \right)$

si tomamos solo la parte real se tiene que

$1-cos\phi -cos\left(n\phi +\phi \right)+cos\phi cos\left(n\phi +\phi \right)+sen\phi sen\left(n\phi +\phi \right)=$

$1-cos\phi +cos\left(n\phi -\phi \right)-cos\left(n\phi +\phi \right)$$=$ $1-cos\phi +2sen\phi sen\phi$

por otra parte para el denominador se tiene:

$\left(1-cos\phi \right)^{2}+sen^{2}\phi =$

$1-2cos\phi +sen^{2}\phi +cos^{2}\phi =$ $2\left(1-cos\phi \right)$

al tomar la parte real de

$1+\left(cos\phi +isen\phi \right)+\left(cos2\phi +isen2\phi \right)+........+\left(cosn\phi +isenn\phi \right)={\frac {1-\left(cos\left(n+1\right)\phi +isen\left(n+1\right)\phi \right)}{1-\left(cos\phi +isen\phi \right)}}$,

sustituir lo encontrado para el numerador (parte real) y el denominador , y utilizar la siguiente identidad

$sen\left({\frac {\phi }{2}}\right)={\sqrt {\frac {1-cos\phi }{2}}}$

tenemos lo siguiente:

$1+cos\phi +cos2\phi +...............+cosn\phi ={\frac {2sen\left({\frac {\phi }{2}}\right)+sen\phi sen\left(n\phi \right)}{2\left(2sen\left({\frac {\phi }{2}}\right)\right)}}={\frac {1}{2}}+{\frac {sen\phi sen\left(n\phi \right)}{2sen\left({\frac {\phi }{2}}\right)}}$

Lo cual es casi a lo que se queria llegar.

---

Realizado por: Dali 00:01 5 oct 2009 (UTC)

---

OTRA DEMOSTRACION DEL EJERCICIO1.1.3 NUMERO 5: 5. Demuestre que

$1+cos\phi +cos2\phi +...............+cosn\phi ={\frac {1}{2}}+{\frac {sen\left(n\phi +{\frac {\phi }{2}}\right)}{2sen\left({\frac {\phi }{2}}\right)}}$,

donde $\phi$ no es un multiplo par de $\pi$.

Esta identidad se le atribuye a Lagrange.

Sugerencia: calcular la parte real de

$1+z+z^{2}+..........+z^{n}$, donde $z=cos\phi +isen\phi$.

Solucion.

Sea $\left(1-Z\right){\displaystyle {\scriptscriptstyle {\displaystyle \sum _{K=0}^{n}z^{k}=}}\sum _{k=0}^{n}z^{k}-\sum _{k=0}^{n}z^{k+1}=1+\sum _{k=1}^{n}z^{k}-\sum _{k=1}^{n}z^{k}-z^{n+1}=1-z^{n+1}}$

y como $z\neq 1$..............& y por ser una serie geometrica la podemos escribir de la siguiente manera

${\displaystyle \sum _{k=0}^{n}z^{k}={\dfrac {1-z^{n+1}}{1-z}}}$

Sea $\theta \in \left(0,2\Pi \right)$, aplicando & con $z=e^{i\theta }\in c/\{1\}$ se tiene lo siguiente

${\displaystyle \sum _{k=0}^{n}e^{ik\theta }={\dfrac {1-e^{i\left(n+1\right)\theta }}{1-e^{i\theta }}}}$

y tomamos partes reales obtenemos ${\displaystyle \sum _{k=0}^{n}\cos k\theta =Re{\dfrac {1-e^{i\left(n+1\right)\theta }}{1-e^{i\theta }}}}$ .............%

desarrolandola se tiene :

${\displaystyle \sum _{k=0}^{n}\cos k\theta =Re{\dfrac {\left[1-e^{i\left(n+1\right)\theta }\right]\left[1-e^{-i\theta }\right]}{\left[1-e^{i\theta }\right]\left[1-e^{-i\theta }\right]}}}$=${\dfrac {1-\cos \theta +\cos n\theta -\cos \left[\left(n+1\right)\theta \right]}{2\left(1-cos\theta \right)}}$ =${\dfrac {1}{2}}+{\dfrac {\cos n\theta -\cos \left[\left(n+1\right)\theta \right]}{2\left(1-\cos \theta \right)}}$.

Con lo cual solo basta probar que

${\dfrac {\cos n\theta -\cos \left[\left(n+1\right)\theta \right]}{2\left(1-\cos \theta \right)}}={\dfrac {\sin \left[\left(n+{\frac {1}{2}}\right)\theta \right]}{2\sin {\frac {\theta }{2}}}}$

Veamos la demostracion

${\dfrac {\cos n\theta -\cos \left[\left(n+1\right)\theta \right]}{2\left(1-\cos \theta \right)}}={\dfrac {\sin \left[\left(n+{\frac {1}{2}}\right)\theta \right]}{2\sin {\frac {\theta }{2}}}}\Longleftrightarrow$

$\left(\cos n\theta -\cos \left[\left(n+1\right)\theta \right]\right)\sin {\frac {\theta }{2}}=\left(1-\cos \theta \right)\sin \left[\left(n+{\frac {1}{2}}\right)\theta \right]\Longleftrightarrow$

$\left(\cos n\theta -\cos n\theta \cos \theta +\sin n\theta \sin \theta \right)\sin {\frac {\theta }{2}}=\left(1-\cos \theta \right)\left(\sin n\theta \cos {\frac {\theta }{2}}+\cos n\theta \sin {\theta \atop 2}\right)\Longleftrightarrow$

$\sin n\theta \sin \theta \sin {\frac {\theta }{2}}=\sin n\theta \cos {\frac {\theta }{2}}-\sin n\theta \cos {\frac {\theta }{2}}\cos \theta$..............#

Si ${\displaystyle \sin n\theta =0}$ la igualdad # es cierta. Si no, es equivalente a

${\displaystyle \cos {\frac {\theta }{2}}\cos \theta +}\sin \theta \sin {\frac {\theta }{2}}=\cos {\frac {\theta }{2}}$.

Lo cual es cierto por la formula de coseno diferencial . Por lo tanto queda demostrado que

${\displaystyle 1+\cos \theta +....................+\cos n\theta ={\dfrac {1}{2}}+{\dfrac {\sin \left(n\theta +{\frac {\theta }{2}}\right)}{2\sin \left({\frac {\theta }{2}}\right)}}}$.

---

Realizado por:Diana Rodriguez Almaraz. 04:47 15 oct 2010 (UTC)

---

DEMOSTRACION ALTERNATIVA DEL EJERCICIO 5 CAP 1.1.3: 5. Demuestre que

$1+cos\theta +cos2\theta +.....+cosn\theta ={\dfrac {1}{2}}+{\dfrac {sen\left(n\theta +{\dfrac {\theta }{2}}\right)}{2sen\left({\dfrac {\theta }{2}}\right)}}$,

donde $\theta$ no es un multiplo par de $\pi$.

Sea $z=\cos \theta +i\sin \theta =e^{i\theta }$

La expresión $1+\cos \theta +...+\cos n\theta$ la podemos expresar como una suma geométrica

${\displaystyle {\scriptscriptstyle {\displaystyle \sum _{K=0}^{n}z^{k}=\sum _{K=0}^{n}\cos k\theta +i\sin k\theta }}}$

Esta serie converge a la expresión:

$i\sin k\theta +\cos {\dfrac {n\theta }{2}}\csc {\dfrac {\theta }{2}}\sin[{\dfrac {\theta (1+n)}{2}}]$

Como nos interesa solamente la parte real de la expresíon omitimos la parte imaginaria.

$Re[i\sin k\theta +\cos {\dfrac {n\theta }{2}}\csc {\dfrac {\theta }{2}}\sin[{\dfrac {\theta (1+n)}{2}}]=\cos {\dfrac {n\theta }{2}}+\csc {\dfrac {\theta }{2}}\sin[{\dfrac {\theta (1+n)}{2}}]$

Reescribiendo la parte real y sabiendo que $\csc x={\dfrac {1}{\sin x}}$

$\cos {\dfrac {n\theta }{2}}\csc {\dfrac {\theta }{2}}\sin[{\dfrac {\theta (1+n)}{2}}]={\dfrac {\cos {\dfrac {n\theta }{2}}+\sin[{\dfrac {\theta (1+n)}{2}}]}{\sin {\dfrac {\theta }{2}}}}$

Ahora bien, por la identidad

$\sin[a]\cos[b]={\dfrac {1}{2}}[\sin[a+b]+\sin[a-b]]$ Con$a={\dfrac {\theta }{2}}+{\dfrac {n\theta }{2}}$ $b={\dfrac {n\theta }{2}}$

Podemos reescrbir la expresión, para la sumas de senos y cosenos del numerador como:

${\dfrac {1}{2}}[\sin[{\dfrac {\theta }{2}}+n\theta ]+\sin {\dfrac {\theta }{2}}]$

Por último simplificando términos y reacomodando, llegamos al resultado

${\dfrac {{\dfrac {1}{2}}\sin[{\dfrac {\theta }{2}}+n\theta ]+\sin {\dfrac {\theta }{2}}}{\sin {\dfrac {\theta }{2}}}}={\dfrac {1}{2}}+{\dfrac {\sin[{\dfrac {\theta }{2}}+n\theta ]}{2\sin {\frac {\theta }{2}}}}$

---

Realizado por: Carlos López Cobá 06:20 26 oct 2010 (UTC)

---

Compleja:ej-cap1.1

esta seccion ej-cap1.1.3

Compleja:ej-cap1.1.4

Compleja:ej-cap1.2

Compleja:ej-cap1.3

Compleja:ej-cap1.4