1. Demuestre que el producto de números complejos cumple con la ley asociativa
Sean  con
con 
Por demostrar 
 = [(ac - bd) + i (bc + ad)](e + i f)\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/37f3be00e91ee5a30f511759482f1ab22d28ee06)
![=[e(ac - bd) - f(bc + ad)] + i [e(bc + ad) + f(ac - bd) = (ace - bde - bcf - adf) + i (bce + ade + acf - bdf)\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/038908935a9fb979e6f1674d75951dd96500012b)
Por otra parte
![z(ws) = (a + i b)[(c + i d)(e + i f)] = (a + i b)[(ce - df) + i (de + cf)]\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ba8441315ba75b800615685131333b9d58e300d2)
![=[a(ce - df) - b(de + cf)] + i [b(ce - df) + a(de + cf)] = (ace - bde - bcf - adf) + i (bce + ade + acf - bdf)\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/108b538ec9ff64dad223e7b48a68abec1981e025)
Entonces se cumple  .
.
--Gabita 22:15 28 sep 2009 (UTC)
1.1.2
1. Demuestre que 
Sean 


![=\frac{1}{c^2 + d^2}\sqrt{a^2 c^2 + a^2 d^2 + b^2 c^2 + b^2 d^2
} = \sqrt{\Bigg [\frac{a^2 (c^2 + d^2)}{(c^2 + d^2)^2}\Bigg ] + \Bigg [\frac{b^2 (c^2 + d^2)}{(c^2 + d^2)^2}\Bigg ]
} = \sqrt{\frac{a^2 + b^2}{c^2 + d^2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4033a07c9b3adb4dd112e1a3bad547e4af5f20a2)
Por otra parte

--Gabita 22:15 28 sep 2009 (UTC)
2. Exprese  de la forma
de la forma 
Por las propiedades  ,
, 

Simplificando, se obtiene:

Resolviendo la divicion de números complejos, de la forma:
 :
:

= .
.
--Josua Da Vinci 23:00 28 sep 2009 (UTC)
5. Sean  tales que cumplen
tales que cumplen  , demuestre que estos tres puntos determinan un triángulo equilátero.
, demuestre que estos tres puntos determinan un triángulo equilátero.
Tenemos que

y, por lo tanto,

De la Figura 1, vemos que cada una de esas normas de números complejos son exactamente los segmentos de recta que constituyen el triángulo ABC, a saber:

De (2) y (3) tenemos que:

Por triángulos semejantes, se tiene que el ángulo  es igual al ángulo
es igual al ángulo  y éste a su vez al ángulo
y éste a su vez al ángulo  , es decir,
, es decir,

== 1.1.7 == Demuestre que en un paralelogramo la suma de los cuadrados de las diagonales es la suma de los cuadrados de los lados.
Recordando Pitágoras c^2 = a^2 + b^2 (para magnitudes reales)
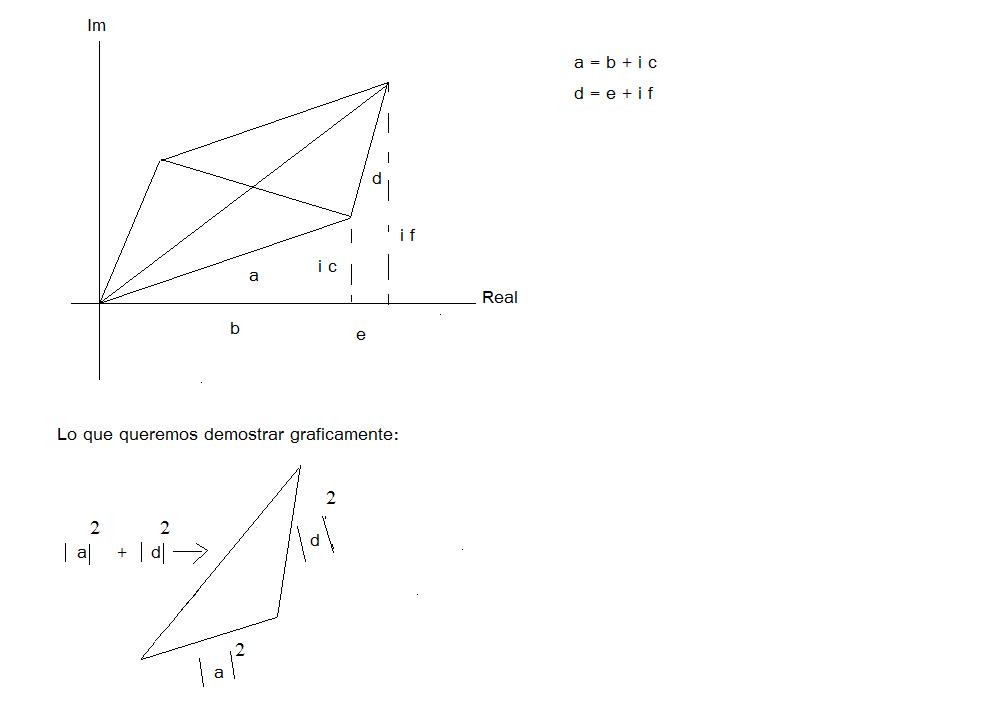
Tomamos dos numeros complejos
a = b + ic
d = e + if
Para poder demostrar que la suma de los cuadrados de los lados sea igual a la suma del cuadrado de las diagonales necesitamos obtener la magnitud de los numeros complejos anteriores "a" y "d".
|a| =  que corresponde a la norma de "a".
|d| =
que corresponde a la norma de "a".
|d| =  que corresponde a la norma de "d".
que corresponde a la norma de "d".
si |a|^2 = b^2 + c^2 y |d|^2 = e^2 + f^2
Ahora definimos la diagonal como |h| con componentes |a| y|d| obtenemos la magnitud de |h| y tenemos
|h|= 
reacomodando.
|h|^2 = |a|^2 + |d|^2 lo que queriamos demostrar.
Por lo tanto tenemos que en un paralelogramo que la suma de los cuadrados de las diagonales son la suma de los cuadrados de los lados.
Con lo anterior hemos concluido nuestra demostración.
--Karla 02:17 29 sep 2009 (UTC)Sanchez
--mfg-wiki 21:27 25 sep 2009 (UTC)
1.1.3
1.1.4
--mfg-wiki 21:27 25 sep 2009 (UTC)




 = [(ac - bd) + i (bc + ad)](e + i f)\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/37f3be00e91ee5a30f511759482f1ab22d28ee06)
![=[e(ac - bd) - f(bc + ad)] + i [e(bc + ad) + f(ac - bd) = (ace - bde - bcf - adf) + i (bce + ade + acf - bdf)\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/038908935a9fb979e6f1674d75951dd96500012b)
![z(ws) = (a + i b)[(c + i d)(e + i f)] = (a + i b)[(ce - df) + i (de + cf)]\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ba8441315ba75b800615685131333b9d58e300d2)
![=[a(ce - df) - b(de + cf)] + i [b(ce - df) + a(de + cf)] = (ace - bde - bcf - adf) + i (bce + ade + acf - bdf)\,](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/108b538ec9ff64dad223e7b48a68abec1981e025)




![=\frac{1}{c^2 + d^2}\sqrt{a^2 c^2 + a^2 d^2 + b^2 c^2 + b^2 d^2
} = \sqrt{\Bigg [\frac{a^2 (c^2 + d^2)}{(c^2 + d^2)^2}\Bigg ] + \Bigg [\frac{b^2 (c^2 + d^2)}{(c^2 + d^2)^2}\Bigg ]
} = \sqrt{\frac{a^2 + b^2}{c^2 + d^2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/4033a07c9b3adb4dd112e1a3bad547e4af5f20a2)






















