Compleja:ej-cap1.1

1.1.1

1. Demuestre que el producto de números complejos cumple con la ley asociativa

Sean $z=a+ib,\quad w=c+id,\quad s=e+if\,\quad$ con $\quad a,b,c,d,e,f\in {\mbox{R}}$

Por demostrar $(zw)s=z(ws)\,$

$(zw)s=[(a+ib)(c+id)](e+if)=[(ac-bd)+i(bc+ad)](e+if)\,$

$=[e(ac-bd)-f(bc+ad)]+i[e(bc+ad)+f(ac-bd)=(ace-bde-bcf-adf)+i(bce+ade+acf-bdf)\,$

Por otra parte

$z(ws)=(a+ib)[(c+id)(e+if)]=(a+ib)[(ce-df)+i(de+cf)]\,$

$=[a(ce-df)-b(de+cf)]+i[b(ce-df)+a(de+cf)]=(ace-bde-bcf-adf)+i(bce+ade+acf-bdf)\,$

Entonces se cumple $(zw)s=z(ws)\,$.

1.1.2

1. Demuestre que $\left|{\frac {z}{w}}\right|={\frac {\left|z\right|}{\left|w\right|}}$

Sean $z=a+ib\quad y\quad w=c+id\,$

$\left|{\frac {z}{w}}\right|=\left|{\frac {a+ib}{c+id}}\right|=\left|{\frac {(a+ib)(c-id)}{(c+id)(c-id)}}\right|$

$=\left|{\frac {(ac+bd)+i(bc-ad)}{c^{2}+d^{2}}}\right|={\sqrt {{\bigg (}{\frac {ac+bd}{c^{2}+d^{2}}}{\bigg )}^{2}+{\bigg (}{\frac {bc-ad}{c^{2}+d^{2}}}{\bigg )}^{2}}}={\frac {1}{c^{2}+d^{2}}}{\sqrt {(ac+bd)^{2}+(bc-ad)^{2}}}$

$={\frac {1}{c^{2}+d^{2}}}{\sqrt {a^{2}c^{2}+a^{2}d^{2}+b^{2}c^{2}+b^{2}d^{2}}}={\sqrt {{\Bigg [}{\frac {a^{2}(c^{2}+d^{2})}{(c^{2}+d^{2})^{2}}}{\Bigg ]}+{\Bigg [}{\frac {b^{2}(c^{2}+d^{2})}{(c^{2}+d^{2})^{2}}}{\Bigg ]}}}={\sqrt {\frac {a^{2}+b^{2}}{c^{2}+d^{2}}}}$

Por otra parte

${\frac {\left|z\right|}{\left|w\right|}}={\frac {\left|a+ib\right|}{\left|c+id\right|}}={\sqrt {\frac {a^{2}+b^{2}}{c^{2}+d^{2}}}}=\left|{\frac {z}{w}}\right|$

---

2. Exprese ${\overline {\left({\frac {\left(2+3i\right)^{2}}{4+i}}\right)}}$de la forma $x+iy$

aqui ya comienza su demostración ...

---

5. Sean $z_{1},z_{2},z_{3}\in \mathbb {C}$ tales que cumplen ${\frac {z_{2}-z_{1}}{z_{3}-z_{1}}}={\frac {z_{1}-z_{3}}{z_{2}-z_{3}}}$, demuestre que estos tres puntos determinan un triángulo equilátero.

Archivo:Comp triang eq2.jpg

Figura 1

Tenemos que

$\left|{\frac {z_{2}-z_{1}}{z_{3}-z_{1}}}\right|=\left|{\frac {z_{1}-z_{3}}{z_{2}-z_{3}}}\right|,\qquad (1)$

y, por lo tanto,

${\frac {|z_{2}-z_{1}|}{|z_{3}-z_{1}|}}={\frac {|z_{1}-z_{3}|}{|z_{2}-z_{3}|}}.\qquad (2)$

De la Figura 1, vemos que cada una de esas normas de números complejos son exactamente los segmentos de recta que constituyen el triángulo ABC, a saber:

$\left.{\begin{matrix}|z_{2}-z_{1}|=A\\|z_{3}-z_{1}|=B=|z_{1}-z_{3}|\\|z_{2}-z_{3}|=C\\\end{matrix}}\right\}\qquad (3)$

De (2) y (3) tenemos que:

${\frac {A}{B}}={\frac {B}{C}}.\qquad (4)$

Por triángulos semejantes, se tiene que el ángulo $\beta$ es igual al ángulo $\gamma$ y éste a su vez al ángulo $\alpha$, es decir,

$\alpha =\beta =\gamma .\qquad (5)$

== 1.1.7 == Demuestre que en un paralelogramo la suma de los cuadrados de las diagonales es la suma de los cuadrados de los lados.

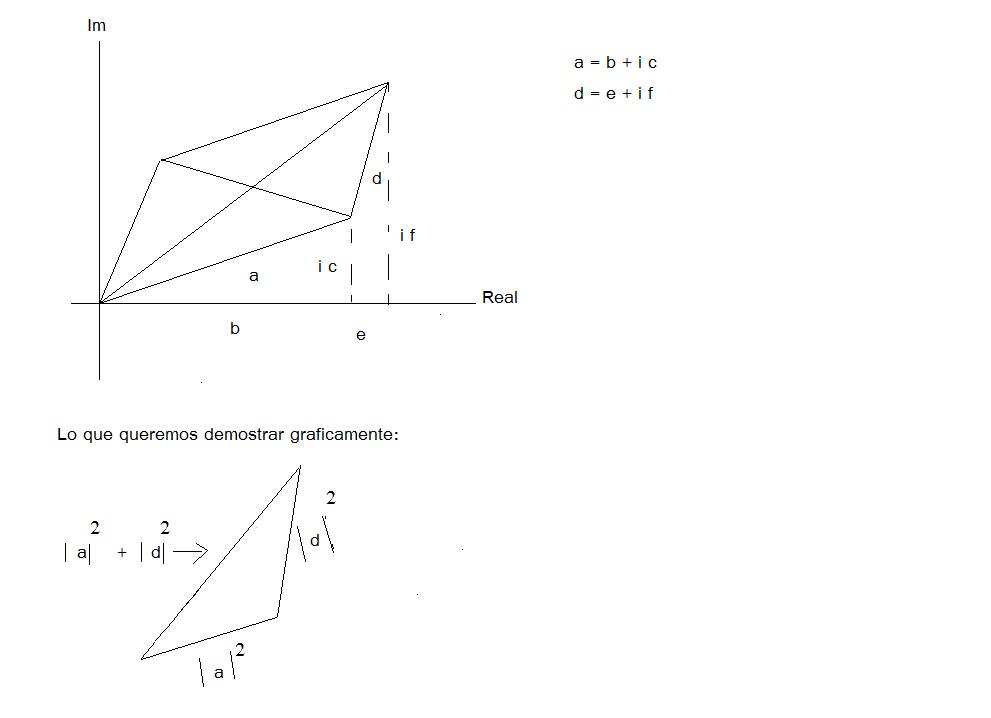
Tomamos dos numeros complejos

a = b + ic d = e + if

Para poder demostrar que la suma de los cuadrados de los lados sea igual a la suma del cuadrado de las diagonales necesitamos obtener la magnitud de los numeros complejos anteriores "a" y "d".

|a|= ${\sqrt {b^{2}+c^{2}}}$ que corresponde a la norma de "a". |d|= ${\sqrt {e^{2}+f^{2}}}$ que corresponde a la norma de "d".

Ahora sumamos el cuadrado de los lados y tenemos

( ${\sqrt {b^{2}+c^{2}}}$ )^2 + ( ${\sqrt {e^{2}+f^{2}}}$ )^2

Haciendo algebra tenemos

e^2+ f^2 + b^2 +c^2

Ahora desarrollamos a^2 + d^2 ( es la suma de los cuadrados de las diagonales)

donde a^2 = (${\sqrt {b^{2}+c^{2}}}$)^2

d^2= (${\sqrt {b^{2}+c^{2}}}$)^2

y a^2 + d^2 = b^2 + c^2 + e^2 + f^2 Suma de los cuadrados de la diagonal

Por otro lado la suma de los cuadrados de los lados b^2+ c^2+ e^2 + f^2 por lo tanto podemos decir que ha quedado demostrado que la suma de los cuadrados de la diagonal es igual a la suma de los cuadrados de los lados.

--mfg-wiki 21:27 25 sep 2009 (UTC)

1.1.4

--mfg-wiki 21:27 25 sep 2009 (UTC)