Compleja:Zill-Cap5.4

Ejercicios del capítulo 5, sección 4 del libro, A First Course in Complex Analysis with Applications de Zill y Shanahan.

---

Sección 5.4

Ejercicio 1

Evalúe la integral de ccontorno C dada en la figura usando una trayectoria alternativa de integración y el teorema fundametal del cálculo para integrales de contorno.

\[ \int_{C} \!(4z-1)\, dz \]

La ruta alternativa es la dibujada en azul que se parametriza del siguiente modo: \[ z(t)=it \;\;\;\;\; -1 \leq t \leq 1 \] \[ dz=i\,dt \]

Que transforma la integral en: \[ \int_{C} \!(4z-1)\, dz = \int_{-1}^{1} \!\left[4(it)-1\right]\, (i)\,dt= \int_{-1}^{1} \!-4t-i\,dt=-4(1-1)/2-i(1--1)=-2i \]

Por el teorema \[ \int_{C} \!(4z-1)\, dz = \frac {4 z^2}{2}-z= 2z^2-z=[2(i)^2-i]-[2(-i)^2--i]=-2-i-(-2+i)=-2-i+2-i=-2i \]

donde se ve que son equivalentes --Tlacaelel Cruz (discusión) 23:39 18 jun 2015 (CDT)

---

Ejercicio 2

In Problems 1 and 2, evaluate the given integral, where the contour C is given in the figure, (a) by using an alternative path of integration and (b) by using Theorem 5.7.

traduccion:

En los problemas 1 y 2 , evaluar la integral dada, donde se da el contorno C en la figura, ( a) mediante el uso de un camino alternativo de integración y ( b ) utilizando el teorema 5.7 .

$\int_{c}e^{z}dz$ donde c esta dada entre los puntos $z0=0$ y $z1=3+i$

insiso a:

para el insiso a necesitamos crear una paremetrisacion de esa curva c

la parametricacion queda:

$z\left(t\right)=3t+i\left(t\right)$ $0\leq t\geq1$

haora con al paremetrisacion podemos calcular al integral de la manera siguiente:

$\int_{c}f\left(z\right)dz=\int_{a}^{b}f\left(z\left(t\right)\right)z^{\prime}\left(t\right)dt$

entonces tenemos

$f\left(z\left(t\right)\right)=e^{3t+it}$

$z\left(t\right)=3t+it$

$z^{\prime}\left(t\right)=3+i$

usando estos resultados podemos escribir la integral de este modo:

$\int_{a}^{b}f\left(z\left(t\right)\right)z^{\prime}\left(t\right)dt=\int_{0}^{1}\left(e^{3t+it}\right)\left(3+i\right)dt$ como el exponente es z y lo que multiplica a la exponencial es z$^{\prime}$ la integral queda $\int e^{z}dz=e^{z}$y regresamos a z en funcion de t y evaluamos

$\int_{c}e^{z}dz=\left[e^{3t+it}\right]_{0}^{1}=\left[e^{3t}e^{it}\right]_{0}^{1}=\left(e^{3}\left(cos\left(1\right)+isen\left(1\right)\right)\right)-\left(1\right)$

insiso b:

para el insiso b necesitamos tener en cuenta el teorema 5.7

el teorema dice lo siguiente:

Supongamos que una función f es continua en un dominio D y F es una primitiva de f en D. Entonces, para cualquier contorno C en D con el punto inicial z0 y punto z1 termina tenemos:

$\int_{c}f\left(z\right)dz=F\left(z_{1}\right)-F\left(z_{0}\right)$

esto funciona para una funcion $f\left(z\right)$que sea analitica

entonces resolvamos la integral de ejercicio mediante este teorema:

$\int_{c}e^{z}dz$ donde $z0=0$ y $z1=3+i$ tenemos una exponencial compleja la cual es entera y analitica en todo el plano complejo por tanto podemos aplicar el teorema 5.7

$f\left(z\right)=e^{z}$ entonces $F\left(z\right)=e^{z}$

entonces usando el teorema tenemos

$\int_{c}e^{z}dz=e^{3+i}-e^{0}=\left(e^{3}\left(cos\left(1\right)+isen\left(1\right)\right)\right)-\left(1\right)$

hemos terminado la integral mediante ytrayectoria y mediante el teorema y llegamos al mismo resultado por lo cual comprovamos que el teorema es sierto si una funcion es analitica y la evaluamos en un segmento podemos calcular solo los puntos final e inicial del segmento si importar la trayectoria

--Martin Flores Molina (discusión) 13:05 15 mayo 2015 (CDT) ----

Ejercicio 3

Evalúa la integral en en el contorno indicado.

$\int_C 2zdz$

$z(t)=2t^3+i(t^4-4t^3+2$

$ -1\leq t\leq1 $

Derivo $z$

$dz=6t^2+i(4t^3-12t^2)$

Sustituyo

$2z= 4t^3+i(2t^4-8t^3+4)$

$2zdz= [4t^3+i(2t^4-8t^3+4)][6t^2+i(4t^3-12t^2] = (-8t^7+56t^6-72t^5-16t^3+48t^2)+i(28t^6-96t^5+24t^2)$

$\int_C 2zdz=\int_{-1}^{1}[(-8t^7+56t^6-72t^5-16t^3+48t^2)+i(28t^6-96t^5+24t^2)]dt = 48+24i$

Nancy Martínez Durán (discusión) 10:56 18 jun 2015 (CDT)

---

Ejercicio 4

Evalúe la integral a lo largo del contorno indicado C

4.- $\intop_{c}2zdz$ , donde C es $z(t)=2cos^{3}\pi t-isen^{2}\frac{\pi}{4}t$ con $0\leqslant t\leqslant2$

Como ya tenemos parametrizada la funcion C en t, solo sustituimos y resolvemos:

$\intop_{0}^{2}2[2cos^{3}\pi t-isen^{2}\frac{\pi}{4}t]dt=4\intop_{0}^{2}cos^{3}\pi tdt-2i\intop_{0}^{2}sen^{2}\frac{\pi}{4}tdt$

Por un lado tenemos

$4\intop_{0}^{2}cos^{3}\pi tdt=4\frac{9sen(\pi t)+sen(3\pi t)}{12\pi}|_{0}^{2}=\frac{9sen(\pi t)+sen(3\pi t)}{3\pi}|_{0}^{2}=\frac{9sen(\pi2)+sen(6\pi)}{3\pi}-\frac{9sen(\pi0)+sen(3\pi0)}{3\pi}=0$

Y que:

$2\intop_{0}^{2}sen^{2}\frac{\pi}{4}tdt=2[\frac{t}{2}-\frac{sen[\pi t/2]}{\pi}]_{0}^{2}=2[\frac{2}{2}-\frac{sen[\pi]}{\pi}]=2$

Finalmente

\[ \intop_{0}^{2}2[2cos^{3}\pi t-isen^{2}\frac{\pi}{4}t]dt=-2i \]

--Fernando Vazquez V. (discusión) 00:12 21 jun 2015 (CDT)

---

Ejercicio 5

Evalue la integral dada

$\int_{0}^{3+i} z^{2}dz$

Aplicaremos el teorema

$\int_{C} f(z)dz = F(z_{1})-F(z_{0})$

Donde

$\int_{0}^{3+i} z^{2}dz=\frac{z^{3}}{3}\mid_{0}^{3+i}$

$\int_{0}^{3+i} z^{2}dz=\frac{(3+i)^{3}}{3}=\frac{18+26i}{3}$

$\int_{0}^{3+i} z^{2}dz=\frac{(3+i)^{3}}{3}=6+\frac{26i}{3}$

Miguel Medina Armendariz (discusión) 17:51 19 jun 2015 (CDT)

---

Ejercicio 6

Evalúa la integral dada $\int_{-2i}^{1} (3z^2 - 4z + 5i)dz$

Separando la integral tenemos:

$= \int_{-2i}^{1} 3z^2 dz - \int_{-2i}^{1} 4z dz + \int_{-2i}^{1} 5i dz$

$= [z^3]_{-2i}^{1} - 2[z^2]_{-2i}^{1} + 5i[z]_{-2i}^{1}$

$= 1 - (-2i)^3 - 2(1 + 4) + 5i (1 + 2i)$

$= 1 - 8i - 10 + 5i - 10$

$= 1 - 20 - 3i = -19 - 3i$

Siendo este nuestro resultado de la forma $a + ib$

Angelina Nohemi Mendoza Tavera (discusión) 14:46 20 jun 2015 (CDT)

---

Ejercicio 7

Ejercicio 7

$\int_{\frac{i}{2}}^{i}=e^{\pi z}dz$

Por cambio de variable $u=\pi z$ , $du=\pi dz$

Por lo que:

$\int_{\frac{i}{2}}^{i}e^{\pi z}dz=\frac{1}{\pi}\int_{\frac{i}{2}}^{i}e^{u}du=\frac{1}{\pi}e^{\pi z}\mid_{\frac{i}{2}}^{i}=\frac{1}{\pi}\left(e^{\pi i}-e^{\frac{\pi i}{2}}\right)$

$=\frac{1}{\pi}\left(\cos\pi+i\sin\pi-\cos\left(\frac{\pi}{2}\right)-\sin\left(\frac{\pi}{2}\right)\right)$

$=\frac{1}{\pi}\left(-1+i0-0-i\right)=-\frac{1}{\pi}-\frac{i}{\pi}$

Entonces:

$\int_{\frac{i}{2}}^{i}e^{\pi z}dz=-\frac{1}{\pi}-\frac{i}{\pi}$

Resuelto por:

Alejandro Juárez Toribio (discusión) 15:57 18 jun 2015 (CDT)

---

Ejercicio 8

Utilizar el teorema 5.4.2 para evaluar la integral dada y ponerla de la forma a+bi

$\int_{-3}^{2i}\left(z^{3}-z\right)dz$

Solución:

Separamos la integral y evaluamos por el Teorema fundamental del calculo para integrales de contorno y así tenemos lo siguiente:

$\int_{-3i}^{2i}z^{3}dz-\int_{-3i}^{2i}zdz$ ... (1)

Primero hacemos la integral de la izquierda, luego la de la derecha de (1) y al final sumaremos para dejarlo de la forma deseada

Recordando que $i^{4}=1$ y que $i^{2}=-1$ lo cual no servirá para cada integral.

$\int_{-3i}^{2i}z^{3}dz=\frac{z^{4}}{4}\mid_{-3i}^{2i}=\frac{1}{4}\left[\left(2i\right)^{4}-\left(-3i\right)^{4}\right]=\frac{1}{4}\left[\left(16\right)-\left(81\right)\right]=\frac{1}{4}\left[16-81\right]=\frac{1}{4}\left[-65\right]=-\frac{65}{4}$ ... (2)

Ahora la segunda integral

$\int_{-3i}^{2i}zdz=\frac{z^{2}}{2}\mid_{-3i}^{2i}=\frac{1}{2}\left[\left(2i\right)^{2}-\left(-3i\right)^{2}\right]=\frac{1}{2}\left[\left(-4\right)-\left(-9\right)\right]=\frac{1}{2}\left[-4+9\right]=\frac{1}{2}\left[5\right]=\frac{5}{2}=\frac{10}{4}$ ...(3)

Recordando que para resolver la segunda integral lo debemos multiplicar por un signo menos por (1)

Ahora solamente sumamos (2) y (3) para dejar lo de la forma a+bi y así obtener el resultado deseado

$-\frac{65}{4}-\frac{10}{4}=\frac{-65-10}{4}=-\frac{75}{4}$

Por lo tanto:

$\int_{-3i}^{2i}\left(z^{3}-z\right)dz=-\frac{75}{4}+0i$

Resuelto por Luis Enrique Martínez Valverde (discusión) 09:52 21 jun 2015 (CDT)

---

Ejercicio 9

Utilice el teorema 5.4.2 para evaluar la integral $\int_{-i/2}^{1-i} \! (2z+1)^2 \,dz$. Escriba la respuesta en la forma $a+ib$.

Teorema fundamental del cálculo para integrales de contorno.

Suponga que una función $f$ es continua en un dominio $D$ y $F$ es una antiderivada de $f$ en $D$.

Entonces, para cualquier contorno $C$ en $D$ con punto inicial $z_{0}$ y punto final $z_{1}$,

\[ \int_{C} \! f(z) \,dz = F(z_{1})-F(z_{0}) \]

$Solución : $

\[ \int_{-i/2}^{1-i} \! (2z+1)^2 \,dz= \int_{-i/2}^{1-i} \! \left( 4z^{2}+4z+1 \right) \,dz = 4 \int_{-i/2}^{1-i} \! z^{2} \,dz + 4 \int_{-i/2}^{1-i} \! z \,dz + \int_{-i/2}^{1-i} \! 1 \,dz \]

Tengo que:

$F(z)= \frac{z^{3}}{3}$ es una antiderivada de $f(z)= z^2$ ya que $F'(z)= z^2$

$F(z)= \frac{z^{2}}{2}$ es una antiderivada de $f(z)= z$ ya que $F'(z)= z$

$F(z)= z $ es una antiderivada de $f(z)= 1$ ya que $F'(z)= 1$

Por tanto; del terorema 5.4.2 tenemos:

\[ 4 \int_{-i/2}^{1-i} \! z^{2} \,dz + 4 \int_{-i/2}^{1-i} \! z \,dz + \int_{-i/2}^{1-i} \! 1 \,dz= 4 \frac{z^{3}}{3} \Big ]_{-i/2}^{1-i} + 4 \frac{z^{2}}{2} \Big ]_{-i/2}^{1-i} + z \Big ]_{-i/2}^{1-i} = \]

\[ \frac{4}{3} \left(-2 -\frac{17}{8} i\right) + 2 \left(-2i +\frac{1}{4} \right) +1 - \frac{i}{2}= \]

\[ - \left( \frac{8}{3} - \frac{17}{6} i \right) - 4i + \frac{1}{2} +1 - \frac{i}{2}= \left( - \frac{8}{3} + \frac{3}{2} \right) + i \left(- \frac{17}{6} - \frac{9}{2} \right) = - \frac{7}{6} - i \frac{22}{3} \]

Finalmente la respuesta en la forma $a+ib$ es:

\[ - \frac{7}{6} - i \frac{22}{3} \]

--Emmanuell Castro Flores (discusión) 21:55 19 jun 2015 (CDT)

---

Ejercicio 13

Utilice el teorema 5.4.2 para evaluar la integral dada.

\[ {\displaystyle \int_{\pi}^{\pi+2i}\sin(\frac{z}{2})dz} \]

Integrando la funcion tenemos que

\[ {\displaystyle \int\sin(\frac{z}{2})dz=2cos(\frac{z}{2})}+c \]

Pero por el teorema 5.4.2

\[ {\displaystyle \int_{\pi}^{\pi+2i}\sin(\frac{z}{2})dz=2\cos(\frac{\pi+2i}{2})-2\cos(\frac{\pi}{2})} \]

Sabemos que $i$ tambien representa una rotacion de $\frac{\pi}{2}$, por lo tanto podemos escribir lo anterior de la siguiente manera

\[ {\displaystyle \int_{\pi}^{\pi+2i}\sin(\frac{z}{2})dz=2\cos(\frac{2\pi}{2})-2\cos(\frac{\pi}{2})=-2} \]

\[ \therefore{\displaystyle \int_{\pi}^{\pi+2i}\sin(\frac{z}{2})dz=-2+i0} \]

Jose Emmanuel Flores Calderón (discusión) 22:08 21 jun 2015 (CDT)

---

Ejercicio 14

utilice el teorema 5.4.2 para evaluar la integral dada . escriba cada respuesta de la forma a+ib

$\intop_{1-2i}^{\pi i}cos(z)dz$

$\intop_{1-2i}^{\pi i}cos(z)dz=sin(z)|_{1-2i}^{\pi i}=sin(\pi i)-sin(1-2i)$

pero lo queremos de la foma a+ib, por lo tanto haremos lo siguiente

$sin(\pi i)=\frac{e^{i(\pi i)}-e^{-i(\pi i)}}{2i}=\frac{e^{-\pi}-e^{\pi}}{2i}=\frac{\frac{1}{e^{\pi}}-e\pi}{2i}=\frac{1-e^{2\pi}}{2ie^{\pi}}=\frac{-(1-e^{2\pi})i}{2e^{\pi}}$

$sin(1-2i)=\frac{e^{i(1-2i)}-e^{-i(1-2i)}}{2i}=\frac{e^{2+i}-e^{-2-i}}{2i}=\frac{e^{2}\left(cos(1)+isin(1)-e^{-2}(cos(-1)-isin(-1)\right)}{2i}=\frac{-e^{2}cos(1)i}{2}+\frac{e^{-2}cos(-1)i}{2}+\frac{e^{2}sin(1)}{2}+\frac{e^{-2}sin(-1)}{2}$

por lo tanto tenemos que el resultado de nuestra integral es

$\intop_{1-2i}^{\pi i}cos(z)dz=sin(z)|_{1-2i}^{\pi i}=sin(\pi i)-sin(1-2i)=\left[\frac{-(1-e^{2\pi})i}{2e^{\pi}}\right]-\left[\frac{-e^{2}cos(1)i}{2}+\frac{e^{-2}cos(-1)i}{2}+\frac{e^{2}sin(1)}{2}+\frac{e^{-2}sin(-1)}{2}\right]=\left[-\frac{e^{2}sin(1)}{2}-\frac{e^{-2}sin(-1)}{2}\right]+i\left[\frac{e^{2}cos(1)}{2}-\frac{e^{-2}cos(-1)}{2}-\frac{(1-e^{2\pi})}{2e^{\pi}}\right]$

--Juan Daniel Rivera Bautista (discusión) 20:52 21 jun 2015 (CDT)

---

Ejercicio 15

Utilize el teorema para evaluar la integral dada.Escriba la respuesta en la forma $a+ib$.

Teorema fundamental del cálculo para integrales de contorno. Suponga que una función $f$ es continua en un dominio $D$ y $F$ es una antiderivada de $f$ en $D$.Entonces , para cualquier contorno $C$ en $D$ con un punto inicial $z_{0}$ y un punto final $z_{1}$.

$\int _{C}f(z)dz=F(z_{1})-F(z_{0})$.

Evaluar: $\int _{i\pi }^{2i\pi }cosh(z)dz$

Por definicion tenemos que: ${\frac {d}{dz}}senh(z)=cosh(z)$

por lo cual tenemos que: $\int _{i\pi }^{2i\pi }cosh(z)dz=senh(z)|_{i\pi }^{2i\pi }$

Ahora bien sabemos que: $senh(z)={\frac {e^{z}-e^{-z}}{2i}}$

sustituyendo : $senh(z)={\frac {e^{2i\pi }-e^{-2i\pi }}{2i}}-{\frac {e^{i\pi }-e^{-i\pi }}{2i}}$

y tomando en cuenta que $cos(-\alpha )=cos(\alpha )$

Evaluando: $e^{2i\pi }=cos(2\pi )+isen(2\pi )=1$

$e^{i\pi }=cos(2\pi )+isen(2\pi )=-1$

Sustituyendo: $senh(z)={\frac {1-1}{2i}}-{\frac {-1-(-1)}{2i}}$

${\frac {0}{2i}}-{\frac {0}{2i}}=0$

Por lo cual nuestra integral evaluada en esos puntos es igual a $0+0i$.

--Anahi Limas (discusión) 22:29 20 jun 2015 (CDT)

---

Ejercicio 19

Utilice el teorema 5.4.2 para evaluar la integral dada.

$\int _{-4i}^{+4i}{\frac {dz}{z^{2}}}$ , C es cualquier contorno que no pase por el origen

Escriba la respuesta en la forma a +ib

Solución

El teorema nos dice que para cualquier contorno C en D(dominio) con punto inicial $z_{0}$ y punto final $z_{1}$

$\int f(z)dz=F(z_{1})-f(z_{0})$

donde : $F(z)=-{\frac {1}{z}}$ es una antiderivada de $f(z)={\frac {1}{z^{2}}}$ ya que $F'(z)={\frac {1}{z^{2}}}=f(z)$

Entonces

$\int _{-4i}^{+4i}{\frac {1}{z^{2}}}dz=-{\frac {1}{z}}\mid _{-4i}^{+4i}=-\left[{\frac {1}{4i}}-\left\{{\frac {1}{-4i}}\right\}\right]=-{\frac {1}{4i}}-{\frac {1}{4i}}=-{\frac {2}{4i}}=-{\frac {1}{2i}}$

simplificando se tiene:

$\int _{-4i}^{+4i}{\frac {1}{z^{2}}}dz=-{\frac {1}{2i}}=-{\frac {1}{2i}}\left({\frac {i}{i}}\right)=-{\frac {i}{2i^{2}}}=-{\frac {i}{-2}}={\frac {i}{2}}$

por lo tanto

$\int _{-4i}^{+4i}{\frac {1}{z^{2}}}dz=0+{\frac {i}{2}}$

Elaborado por Ricardo García Hernández--Ricardo Garcia Hernandez (discusión) 23:30 20 jun 2015 (CDT)

---

Ejercicio 22

Utilizar integración por partes para evaluar la integral. Escribir cada respuesta en la forma $a+bi$

$\intop_{0}^{i}zsenzdz$

Por tanto, utilizando el teorema: $\int_{z_{0}}^{z_{1}}f(z)g'(z)dz=f(z)g'(z)|_{z_{0}}^{z_{1}}-\int_{z_{0}}^{z_{1}}f'(z)g(z)dz$ se puede evaluar la integral de la siguiente forma:

Primero escojemos nuestras funciones $g(z)$ y $f(z)$ de la mejor manera. En este caso conviene usar:

$f(z)=z$ ; $f'(z)=1dz$

$g(z)=-cosz$ ; $g'(z)=senz$

Ahora podemos escribir entonces:

$\intop_{0}^{i}zsenzdz=-zcosz+\intop_{0}^{i}coszdz=[-zcosz+senz]_{0}^{i}$

$=(-icosi+seni)-(-(0)cos0+sen0)=(-icosi+seni)$

Usamos las identidades exponenciades del sen y coseno y sustituimos

$=i(\frac{e^{ii}+e^{-ii}}{2})+(\frac{e^{ii}-e^{-ii}}{2i})$

$=i(\frac{e^{-1}+e^{1}}{2})+(\frac{e^{-1}-e^{1}}{2i})(\frac{-2i}{-2i})=i(\frac{e^{-1}+e^{1}}{2})+(\frac{-2ie^{-1}+2ie^{1}}{4})$

$=\frac{ie^{-1}}{2}+\frac{ie^{1}}{2}-\frac{2ie^{-1}}{4}+\frac{2ie^{1}}{4}$

$=\frac{ie^{-1}}{2}+\frac{ie^{1}}{2}-\frac{ie^{-1}}{2}+\frac{ie^{1}}{2}=\frac{ie^{-1}}{2}+\frac{ie^{1}}{2}-\frac{2ie^{-1}}{4}+\frac{2ie^{1}}{4}=-\frac{i}{e^{1}}+ie^{1}=i(-\frac{1}{e^{1}}+e^{1})=i2.350402$

Lo cual es un resultado de la forma $a+bi$ donde $a=0$

--A. Martín R. Rabelo (discusión) 20:14 21 jun 2015 (CDT)

---

Ejercicio 23

Utilice la integración por partes para evaluar la integral.

$\int _{i}^{1+i}ze^{z}dz$

Escriba la respuesta en la forma a +ib

Solución

$\int _{i}^{1+i}ze^{z}dz=ze^{z}\mid _{i}^{1+i}-\int _{i}^{1+i}e^{z}dz$

$\int _{i}^{1+i}ze^{z}dz=[\left[1+i\right]e^{1+i}-ie^{i}]-\int _{i}^{1+i}e^{z}dz$

$\int _{i}^{1+i}ze^{z}dz=[\left[1+i\right]e^{1+i}-ie^{i}]-\left[e^{1+i}-e^{i}\right]$

Simplificando se tiene:

$\int _{i}^{1+i}ze^{z}dz=[ie^{1+i}-ie^{i}+e^{i}]=-0.905582+1.76986i$

Este último resultado numerico irracional se obtuvo con el comando de programa de Mathematica : $N[ie^{1+i}-ie^{i}+e^{i}]$ entonces:

$\int _{i}^{1+i}ze^{z}dz=-0.905582+1.76986i$

Elaborado por Ricardo García Hernández--Ricardo Garcia Hernandez (discusión) 23:52 20 jun 2015 (CDT)

---

Ejercicio 25

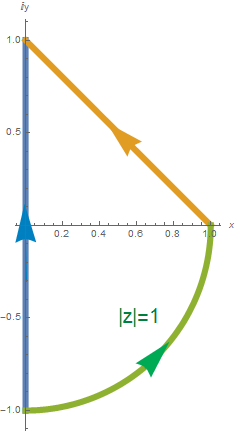
Utilizar el teorema 5.4.2 para evaluar la integral $\int_C \frac{1}{4 z^{1/2}}dz$ es la rama principal de la función raíz cuadrada, donde $C$ es el arco de la circunferencia $z=4e^{i\phi }$ con $\phi \epsilon [{\frac {-\pi }{2}},{\frac {\pi }{2}}]$. Escribir en forma $a+ib$.

Usando la parametrización dada por la circunferencia tenemos que $z=4e^{i\phi }$ y $dz=4ie^{i\phi }d\phi$

Por lo que si sustituimos este resultado en la integral tenemos que

$\int _{C}{\frac {1}{4z^{1/2}}}dz=\int _{C}{\frac {4ie^{i\phi }}{4(4ie^{i\phi })^{\frac {1}{2}}}}d\phi =\int _{C}i{\frac {e^{\frac {i\phi }{2}}}{2}}d\phi$

Por lo que cuando resolvemos la integral, sabiendo que es continua en el dominio aseguramos que por el teorema fundamental del cálculo para integrales de contorno que

$\int f(z)dz=F(z_{1})-F(z_{2})$

por lo que tenemos que tenemos que

${\frac {i}{2}}\int _{C}e^{\frac {i\phi }{2}}d\phi =({\frac {i}{2}})({\frac {1}{\frac {i}{2}}})e^{\frac {i\phi }{2}}|_{\frac {-\pi }{2}}^{\frac {\pi }{2}}=e^{\frac {i\pi }{4}}-e^{\frac {-i\pi }{4}}$

Escribiendo el resultado de la forma a+bi observamos que la solución anterior tiene la forma de un seno en función de exponentes multiplicado por un 2i, es decir que

$e^{\frac {i\pi }{4}}-e^{\frac {-i\pi }{4}}=2isen({\frac {\pi }{4}})=2i{\frac {\sqrt {2}}{2}}={\sqrt {2}}i$

Por lo que $\int_C \frac{1}{4 z^{1/2}}dz$ para el arco de la circunferencia $z=4e^{i\phi }$ con $\phi \epsilon [{\frac {-\pi }{2}},{\frac {\pi }{2}}]$.

$\int_C \frac{1}{4 z^{1/2}}dz=\sqrt{2}i$

--Pablo (discusión) 11:18 21 jun 2015 (CDT)

---

Ejercicio 26

Utilizar el teorema 5.4.2 para evaluar la integral $\int_C3z^{1/2}dz$, donde $C$ es el segmento de recta entre $z_0=1$ y $z_1=9i$. $z^{1/2}$ es la rama principal de la función raíz cuadrada. Escribir en forma $a+ib$.

Sol. Buscamos una antiderivada $F(z)$ de la función $f(z)$ tal que $F'(z)=f(z)$. Proponemos $F(z)=2z^{3/2}$ y comprobamos derivando

$\dfrac{d}{dz}F(z)=\dfrac{d}{dz}2z^{3/2}=2\frac{3}{2}z^{3/2-1}=3z^{1/2}$

Así, procedemos hacer uso del Teorema fundamental de cálculo para integrales de contorno:

$\int_C3z^{1/2}dz=F(z)|_{z_0}^{z_1}=F(z_1)-F(z_0)=2z_1^{3/2}-2z_0^{3/2}=2(9i)^{3/2}-2(1)^{3/2}=2(9i)^{3/2}-2$

Para $(9i)^{3/2}$ utilizamos la fórmula multivaluada para las potencias y elegimos a $k=0$ para escoger la rama principal.

$w_k=^n\sqrt{r}[\cos (\dfrac{\theta +2k\pi}{n})+i\sin (\dfrac{\theta +2k\pi}{n})]$

Con $n=3/2$, $r=9$, $\theta =\dfrac{\pi}{2}$ y $k=0$

$w_0=9^{3/4}[\cos (\dfrac{\pi /2}{3/2})+i\sin (\dfrac{\pi /2}{3/2})]\approx 5.2(\cos \frac{\pi}{3}+i\sin \frac{\pi}{3})\approx 5.2(\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2})\approx 2.6+i4.5$

Sustituyendo

$\int_C3z^{1/2}dz\approx 2(2.6+i4.5)-2=5.2+i9-2=3.2+i9$

$\int_C3z^{1/2}dz\approx 3.2+i9$

Oscar Javier Gutierrez Varela (discusión) 22:11 18 jun 2015 (CDT)

---

Ejercicio 29

teorema:

suponga que una función $f$es continua en un dominio $D$ y $F$ es anti-derivada de $f$ en $D$.Entonces, para cualquier contorno$C$en $D$ con punto inicial $z_{0}$y un punto final $z_{1}$

$\int_{C}f(z)dz=F(z_{1})-F(z_{0}).$

sea $\alpha=a+ib$ una constante compleja.

a) aplique el teorema para evaluar $\int_{x_{0}}^{x}e^{\alpha z}dz$ donde $x_{0}$ y $x$ son los valores reales.

b)Explique como el inciso a) y el teorema con la parametrizacion $z(t)=t,\;x_{0}\leq t\leq x$ se puede usar para deducir la formula integral (real)

$\int e^{ax}\cos bxdx=\frac{e^{ax}(a\cos bx+b\sin bx}{a^{2}+b^{^{2}}}+C$

sea $f(z)=e^{\alpha z}$ entonces su anti derivada es$F(z)=\frac{1}{\alpha}e^{\alpha z}$ ya que $F'(z)=e^{\alpha z}=f(z)$

así por el teorema tenemos:

$\int_{C}f(z)dz=\int_{x_{0}}^{x}e^{\alpha z}dz=F(x)-F(x_{0})=\frac{1}{\alpha}[e^{\alpha x}-e^{\alpha x_{0}}]=\frac{1}{a+ib}[e^{x(a+ib)}-e^{x_{0}(a+ib)}]=\frac{1}{a+ib}[e^{ax}e^{ibx}-e^{ax_{0}}e^{ibx_{0}}]$

multiplicando por el conjugado de $\alpha$ tenemos $(\alpha^{c}=a-ib)$

$\frac{a-ib}{(a+ib)(a-ib)}[e^{ax}e^{ibx}-e^{ax_{0}}e^{ibx_{0}}]=\frac{a-ib}{a^{^{2}}+b^{2}}[e^{ax}e^{ibx}-e^{ax_{0}}e^{ibx_{0}}]=\frac{a-ib}{a^{2}+b^{2}}\{e^{ax}[\cos bx+i\sin bx]-e^{ax_{0}}[\cos bx_{0}+i\sin bx_{0}]\}$

desarrollando la multiplicación de los denominadores tenemos:

$\frac{1}{a^{2}+b^{2}}\{e^{ax}[a\cos bx+ia\sin bx]-e^{ax_{0}}[a\cos bx_{0}+ia\sin bx_{0}+e^{ax}[-ib\cos bx-i^{2}b\sin bx]+e^{ax_{0}}[ib\cos bx_{0}+i^{2}b\sin bx_{0}]\}$

distinguiendo términos reales e imaginarios, y desarrollando:

$\frac{1}{a^{2}+b^{2}}\{e^{ax}[a\cos bx+b\sin bx]+e^{ax}[-ib\cos bx+ia\sin bx]-e^{ax_{0}}[a\cos bx_{0}+b\sin bx_{0}]+e^{ax_{0}}[-ia\sin bx_{0}+ib\cos bx_{0}]\}$

$\frac{1}{a^{2}+b^{2}}\{e^{ax}[(a\cos bx+b\sin bx)+(ia\sin bx-ib\cos bx)]-e^{ax_{0}}[(a\cos bx_{0}+b\sin bx_{0})+(ia\sin bx_{0}-ib\cos bx_{0})]\}$

así:

$\int_{x_{0}}^{x}e^{\alpha z}dz=\frac{1}{a^{2}+b^{2}}\{e^{ax}[(a\cos bx+b\sin bx)+(ia\sin bx-ib\cos bx)]-e^{ax_{0}}[(a\cos bx_{0}+b\sin bx_{0})+(ia\sin bx_{0}-ib\cos bx_{0})]\}$

podemos ver que:

la parte Real de $\int_{x_{0}}^{x}e^{\alpha z}dz$ es:

$\frac{1}{a^{2}+b^{2}}\{e^{ax}(a\cos bx+b\sin bx)-e^{ax_{0}}(a\cos bx_{0}+b\sin bx_{0})\}$

la parte imaginaria de $\int_{x_{0}}^{x}e^{\alpha z}dz$ es:

$\frac{i}{a^{2}+b^{2}}\{e^{ax}(a\sin bx-b\cos bx-e^{ax_{0}}(a\sin bx_{0}-b\cos bx_{0})\}$

si tomamos la parametrizacion $z(t)=t,\;x_{0}\leq t\leq x$ entonces

$z'(t)=1dt$

$\Longrightarrow\int e^{\alpha z}dz=\int_{x_{0}}^{x}e^{\alpha t}dt=\int_{x_{0}}^{x}e^{(a+ib)t}dt=\int_{x_{0}}^{x}e^{at}e^{ibt}dt=\int_{x_{0}}^{x}e^{at}(\cos bt+i\sin bt)dt$

pero:

$\int_{x_{0}}^{x}e^{at}(\cos bt+i\sin bt)dt=\int_{x_{0}}^{x}e^{at}(\cos bt)dt+\int_{x_{0}}^{x}e^{at}i(\sin bt)dt$

y tomando solo la integral real:

$\int_{x_{0}}^{x}e^{at}(\cos bt)dt$ y por el resultado anterior:

$\int_{x_{0}}^{x}e^{at}(\cos bt)dt=\frac{1}{a^{2}+b^{2}}\{e^{ax}(a\cos bx+b\sin bx)-e^{ax_{0}}(a\cos bx_{0}+b\sin bx_{0})\}$

de aqui que:

$\int e^{ax}(\cos bx)dx=\frac{1}{a^{2}+b^{2}}\{e^{ax}(a\cos bx+b\sin bx)\}+C$

--Francisco Medina Albino (discusión) 23:30 18 jun 2015 (CDT)

---

Ejercicio 30

Encuentre a $\int e^{ax}\sin bx dx$

\[ \int e^{(a + bi)x} dx =\dfrac{e^{(a + bi)x}}{a+bi}\]

o bien

\[ \int e^{ax}(\cos bx + i \sin bx) dx = \dfrac {e^{ax}(cos bx + i \sin bx)}{a + ib}= \dfrac {e^{ax}(cos bx + i \sin bx)(a - i b)}{a^{2} + b^{2}}\]

Entonces

\[ \int e^{ax}\sin bx dx= \dfrac {e^{ax}(cos bx + i \sin bx)(a - i b)}{a^{2} + b^{2}}\]

--Esther Sarai (discusión) 23:20 20 jun 2015 (CDT)Esther Sarai