Diferencia entre revisiones de «Análisis de Fourier, pulsos en una cuerda»
Sin resumen de edición |
Sin resumen de edición |
||
| (No se muestran 11 ediciones intermedias de 2 usuarios) | |||
| Línea 1: | Línea 1: | ||
== Jean-Baptiste Joseph Fourier. == | == Jean-Baptiste Joseph Fourier. == | ||
Jean-Baptiste Joseph Fourier (Auxerre, Francia, 21 de marzo de 1768 - París, 16 de mayo de 1830), matemático y físico francés conocido por sus trabajos sobre la descomposición de funciones periódicas en series trigonométricas convergentes llamadas Series de Fourier, método con el cual consiguió resolver la ecuación del calor. La transformada de Fourier recibe su nombre en su honor. Fue el primero en dar una explicación científica al efecto invernadero en un tratado. En su honor un asteroide que fue descubierto en 1992 por el astrónomo belga Eric Walter Elst fue designado como Fourier .<ref>http://matematicos.matem.unam.mx/otras-efemerides-de-todo-el-mes-de-marzo/1270-21-de-marzo-natalicio-de-jean-baptiste-joseph-fourier</ref> | Jean-Baptiste Joseph Fourier (Auxerre, Francia, 21 de marzo de 1768 - París, 16 de mayo de 1830), matemático y físico francés conocido por sus trabajos sobre la descomposición de funciones periódicas en series trigonométricas convergentes llamadas Series de Fourier, método con el cual consiguió resolver la ecuación del calor. La transformada de Fourier recibe su nombre en su honor. Fue el primero en dar una explicación científica al efecto invernadero en un tratado. En su honor un asteroide que fue descubierto en 1992 por el astrónomo belga Eric Walter Elst fue designado como Fourier .<ref>http://matematicos.matem.unam.mx/otras-efemerides-de-todo-el-mes-de-marzo/1270-21-de-marzo-natalicio-de-jean-baptiste-joseph-fourier</ref> | ||
[[Archivo:Joseph Fourier.png.jpg|miniaturadeimagen|centro|Conquístame con unas series que ni Netflix tenga: Joseph Fourier.]] | [[Archivo:Joseph Fourier.png.jpg|miniaturadeimagen|centro|Figura1: Conquístame con unas series que ni Netflix tenga: Joseph Fourier.]] | ||
== Formalismo General del Análisis de Fourier. == | |||
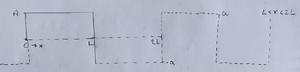
== Análisis de Fourier | [[Archivo:Cuuerda1.png|miniaturadeimagen|derecha|Figura2:Cuerda fijada en ambos extremos.]] | ||
[[Archivo:Cuuerda1.png|miniaturadeimagen|derecha|Cuerda fijada en ambos extremos.]] | |||
Supongamos que tenemos una cuerda de longitud L fija en sus dos extremos. Entonces, sabemos | Supongamos que tenemos una cuerda de longitud L fija en sus dos extremos. Entonces, sabemos | ||
por lo que hemos aprendido, que comenzará a oscilar en un número infinito de modos normales, que son ondas estacionarias. Permitiendo la elección tanto de la amplitud como de fase de un | por lo que hemos aprendido, que comenzará a oscilar en un número infinito de modos normales, que son ondas estacionarias. Permitiendo la elección tanto de la amplitud como de fase de un | ||
| Línea 11: | Línea 10: | ||
La ecuación es: | La ecuación es: | ||
\begin{equation} | \begin{equation} | ||
y(x,t)= \sum_{n=1}^{\infty} B_{n} \sin(\kappa_{n}x) \cos(\omega_{n} t) | y(x,t)= \sum_{n=1}^{\infty} B_{n} \sin(\kappa_{n}x) \cos(\omega_{n} t) | ||
\end{equation} | \end{equation} | ||
| Línea 31: | Línea 30: | ||
\underbrace{\sum_{1}^{\infty} B_{m} \sin(mx)}_{3c} | \underbrace{\sum_{1}^{\infty} B_{m} \sin(mx)}_{3c} | ||
\end{equation} | \end{equation} | ||
Cabe resaltar que esta | Cabe resaltar que esta $x$ está en radianes. | ||
Así que nuestra tarea ahora es encontrar los valores de $A$ y $B$ si conoce la función $ | Así que nuestra tarea ahora es encontrar los valores de $A$ y $B$ si conoce la función $ | ||
f(x) $ y construiremos la ''receta'' que nos permite calcular los valores de $A$ y los valores de $B$. | f(x) $ y construiremos la ''receta'' que nos permite calcular los valores de $A$ y los valores de $B$. | ||
Lo primero que hacemos para encontrar $A_{0}$ es tomar la integral $ \int_{-\pi}^{\pi} $ y veremos que para $( | Lo primero que hacemos para encontrar $A_{0}$ es tomar la integral $ \int_{-\pi}^{\pi} $ y veremos que para $(3b)$ y $(3c)$ son cero. | ||
Por lo que nos queda de la siguiente forma el primer término de $(3)$ | Por lo que nos queda de la siguiente forma el primer término de $(3)$ | ||
| Línea 48: | Línea 47: | ||
¿Cómo vamos a calcular los otros valores para $A$? Lo que hacemos es tomar la integral, con los mismos intervalos que hace un momento, de $ \int_{-\pi}^{\pi} $ y veremos que para $(3a)$ y $(3c)$ son cero, también será cero para $(3b)$ excepto cuando $m=n$. | ¿Cómo vamos a calcular los otros valores para $A$? Lo que hacemos es tomar la integral, con los mismos intervalos que hace un momento, de $ \int_{-\pi}^{\pi} $ y veremos que para $(3a)$ y $(3c)$ son cero, también será cero para $(3b)$ excepto cuando $m=n$. | ||
Entonces, | Entonces, | ||
\ | \[ | ||
\int_{-\pi}^{\pi} \cos(nx) dx | \int_{-\pi}^{\pi} \cos(nx) dx | ||
\ | \] | ||
Para $ n=1,2,3... $ | Para $ n=1,2,3... $ | ||
Si nos fijamos | Si nos fijamos en el término de $(3b)$, nos daremos cuenta que es $0$ excepto cuando $m=n$ (como lo mencionamos anteriormente). Cuando $m=n$, obtenemos | ||
\begin{equation} | \begin{equation} | ||
\int_{-\pi}^{\pi} \cos^{2}(mx)dx=\pi | \int_{-\pi}^{\pi} \cos^{2}(mx)dx=\pi | ||
| Línea 63: | Línea 62: | ||
Ya sabemos cómo calcular $A_{0}$ y sabemos cómo calcular los valores para $A_{m}$. | Ya sabemos cómo calcular $A_{0}$ y sabemos cómo calcular los valores para $A_{m}$. | ||
Ahora, encontraremos valores para $B$. Integraremos ambos lados de la integral entre $-\pi$ y $\pi$ multiplicado por el $\sin(nx)dx$ y cuando lo hagamos, veremos exactamente lo mismo que teníamos en $(3)$, veremos que $(3a)$ será 0 al igual que $(3b)$, $(3c)$ siempre será 0 excepto cuando $m=n$, entonces en $(3c)$ obtendremos el cuadrado del seno, y la integral del $\sin^{2}$ será $\pi$ casi igual que la integral ( | Ahora, encontraremos valores para $B$. Integraremos ambos lados de la integral entre $-\pi$ y $\pi$ multiplicado por el $\sin(nx)dx$ y cuando lo hagamos, veremos exactamente lo mismo que teníamos en $(3)$, veremos que $(3a)$ será $0$ al igual que $(3b)$, $(3c)$ siempre será $0$ excepto cuando $m=n$, entonces en $(3c)$ obtendremos el cuadrado del seno, y la integral del $\sin^{2}$ será $\pi$ casi igual que la integral $(6)$. Entonces, vemos que también tenemos la ''receta'' para encontrar todos los valores de $B_{m}$ | ||
\begin{equation} | \begin{equation} | ||
\boxed{ B_{m}= \int_{-\pi}^{\pi} f(x) \sin(mx) dx } | \boxed{ B_{m}= \int_{-\pi}^{\pi} f(x) \sin(mx) dx } | ||
| Línea 72: | Línea 71: | ||
Hay que tener en cuenta que siempre que tengamos una integral de $-\pi$ a $\pi$, le podemos cambiar lo límites de integración, si se prefiere, de $0$ a $2\pi $, porque la función es periódica. | Hay que tener en cuenta que siempre que tengamos una integral de $-\pi$ a $\pi$, le podemos cambiar lo límites de integración, si se prefiere, de $0$ a $2\pi $, porque la función es periódica. | ||
Si observamos estas tres recetas: $(5),( | Si observamos estas tres recetas: $(5),(7),(8)$, podemos eliminar $(5)$ porque si hacemos que $m=0$ en $(7)$ ($m$ va de $1,2,3,4,5$), si también incluimos $m=0$ en $(7)$, obtendremos exactamente lo mismo que tenemos en $(5)$ porque cuando $m=0$, el coseno es uno, entonces $(5)$ y $(7)$ son idénticos. | ||
Esa es la única razón por la que llamamos al término $( | Esa es la única razón por la que llamamos al término $(3a)$ constante que es $\frac{A_{0}}{2}$, podríamos haberlo llamado $C$ porque después de todo una constante es una constante; esta constante es el valor promedio de la función, entonces necesitaríamos esta $C$ en $(5)$ y tendríamos $\frac{1}{2 \pi}$ y, por lo tanto, necesitaríamos 3 recetas para hacer el ''análisis de Fourier'', mientras que si definimos esta constante como $\frac{A_{0}}{2}$, solo necesitamos 2, pero $\frac{A_{0}}{2}$ es una constante y es el valor promedio de la función sobre el periodo. | ||
Todo esto nos puede parecer un poco opaco por ahora y espero que quede claro en este trabajo cuando pongamos a trabajar este análisis de Fourier. | Todo esto nos puede parecer un poco opaco por ahora y espero que quede claro en este trabajo cuando pongamos a trabajar este análisis de Fourier. | ||
Lo que hemos visto aquí (y así es como quiero que lo veas), | Lo que hemos visto hasta aquí (y así es como quiero que lo veas), es simplemente una receta y cuando usemos esta receta, la ejecutamos y no siempre nos preguntamos por qué la receta es así, al contrario, usamos las recetas (una analogía en la cocina) para cocinar una deliciosa comida, agua y/o postres. | ||
== Análisis de Fourier para una cuerda pulsada. == | |||
Así que ahora me gustaría volver a la cuerda pulsada, pero primero quiero echarle un vistazo de cerca en el momento $t=0$, y lo que voy a hacer es puntearla de una manera muy inusual. Hay una razón por la cual lo hago de manera tan inusual, porque es factible hacer el ''análisis de Fourier'', así que ahora tengo una cuerda que está fija entre $0$ y $L$ y la voy a acoplar de una manera ''extraña'', es decir, | Así que ahora me gustaría volver a la cuerda pulsada, pero primero quiero echarle un vistazo de cerca en el momento $t=0$, y lo que voy a hacer es puntearla de una manera muy inusual. Hay una razón por la cual lo hago de manera tan inusual, porque es factible hacer el ''análisis de Fourier'', así que ahora tengo una cuerda que está fija entre $0$ y $L$ y la voy a acoplar de una manera ''extraña'', es decir, | ||
[[Archivo:Cuerda2.png| | [[Archivo:Cuerda2.png|miniaturadeimagen|centro|Figura 3.]] | ||
Lo estoy forzando a un cuadrado para la cuerda, si quiero usar el ''análisis de Fourier'' y verán cómo lo voy a hacer porque necesito una función periódica y la que aparece en la imagen de aquí arriba no es periódica, así que la haré periódica. La forma para hacerla periódica es la siguiente: supongo que la función es realmente así, | Lo estoy forzando a un cuadrado para la cuerda, si quiero usar el ''análisis de Fourier'' y verán cómo lo voy a hacer porque necesito una función periódica y la que aparece en la imagen de aquí arriba no es periódica, así que la haré periódica. La forma para hacerla periódica es la siguiente: supongo que la función es realmente así, | ||
[[Archivo:Cuerda2.1.png|miniaturadeimagen|centro|Función periódica.]] | [[Archivo:Cuerda2.1.png|miniaturadeimagen|centro|Figura 4:Función periódica.]] | ||
Agregué esto: llegué a $2L$ pero voy mucho más allá, así que lo vuelvo a definir entre $0$ y $2L$ y eso ya periódico. Hay que notar que el patrón hacia arriba y hacia abajo es periódico, por lo que significa que mi periodo es $2L$ y al hacerlo, vemos que $\frac{A_{0}}{2}=0$ porque el valor promedio de esta función, que ahora está definido entre $0$ y $2 L$ y mucho más allá de $2L$ y por debajo de $0$, tiene un valor promedio de $0$ y, por lo tanto, mi función $f (x)$ puede escribirse como una función $y(x)$. | Agregué esto: llegué a $2L$ pero voy mucho más allá, así que lo vuelvo a definir entre $0$ y $2L$ y eso ya periódico. Hay que notar que el patrón hacia arriba y hacia abajo es periódico, por lo que significa que mi periodo es $2L$ y al hacerlo, vemos que $\frac{A_{0}}{2}=0$ porque el valor promedio de esta función, que ahora está definido entre $0$ y $2 L$ y mucho más allá de $2L$ y por debajo de $0$, tiene un valor promedio de $0$ y, por lo tanto, mi función $f (x)$ puede escribirse como una función $y(x)$. | ||
Ahora, quiero expresar esta forma en series de Fourier, pero antes de poder hacer eso, tengo que hacer algunos cambios en nuestra ''receta'' porque en la ''receta'' tenemos radianes en $(3)$ y los radianes son ''manzanas'' y en la imagen con la función periódica tenemos $x$, pero no está en radianes, es decir, metros y los metros son ''peras''. | Ahora, quiero expresar esta forma en series de Fourier, pero antes de poder hacer eso, tengo que hacer algunos cambios en nuestra ''receta'' porque en la ''receta'' tenemos ''radianes'' en $(3)$ y los ''radianes'' son ''manzanas'' y en la imagen con la función periódica (Figura 4) tenemos $x$, pero no está en ''radianes'', es decir, ''metros'' y los ''metros'' son ''peras''. | ||
Dicho esto, los ''radianes'' son ''manzanas'' y los ''metros'' son ''peras'', pero ¿qué debo hacer para convertir las peras en manzanas? Tengo que tomar la antigua $x$ que estaba en ''radianes'', que es la que tengo en (6) y esa es la que tengo en $(3b)$, voy a reemplazar eso en ese formalismo de la vieja $ x (radianes) \Rightarrow \frac{x \pi}{L}(metros) $. | |||
Y esta última $x$ ya está en metros. Podemos ver que, si mi $x$ ahora se convierte en $2L$, entonces esto se ha movido a $\pi$ radianes. | Y esta última $x$ ya está en $metros^{-1}$. Podemos ver que, si mi $x$ ahora se convierte en $2L$, entonces esto se ha movido a $\pi$ radianes. | ||
Con todo esto, ya podemos manejarlo de la misma manera porque ya tenemos ''manzanas'' en la imagen con función periódica y tenemos ''manzanas'' en las demás ecuaciones, eso significa que ahora mi serie de Fourier se va a parecer mucho a lo que tenemos en $(3)$, pero prefiero escribirlo nuevamente, nos queda | Con todo esto, ya podemos manejarlo de la misma manera porque ya tenemos ''manzanas'' en la imagen con función periódica y tenemos ''manzanas'' en las demás ecuaciones, eso significa que ahora mi serie de Fourier se va a parecer mucho a lo que tenemos en $(3)$, pero prefiero escribirlo nuevamente, nos queda | ||
| Línea 102: | Línea 102: | ||
\frac{1}{\pi} \int_{-\pi}^{\pi} \hspace{0.3cm}; \int_{0}^{2L} \hspace{0.3cm}; \int_{-L}^{L} | \frac{1}{\pi} \int_{-\pi}^{\pi} \hspace{0.3cm}; \int_{0}^{2L} \hspace{0.3cm}; \int_{-L}^{L} | ||
\end{equation} | \end{equation} | ||
Lo podemos expresar como cualquiera de las integrales de $( | Lo podemos expresar como cualquiera de las integrales de $(10)$. | ||
Tengo que cambiar este $\frac{1}{\pi}$ que tenemos al frente de $( | Tengo que cambiar este $\frac{1}{\pi}$ que tenemos al frente de $(10)$ porque eso fue el resultado de la integral $(6)$ y si hacemos la integral, habremos encontrado $L$ y no $\pi$, esto es la mitad del periodo y la mitad del periodo de nuestra función es $L$, por lo que debe cambiarse a | ||
\begin{equation} | \begin{equation} | ||
\frac{1}{\pi} \rightarrow \frac{1}{L} \int_{0}^{2L} | \frac{1}{\pi} \rightarrow \frac{1}{L} \int_{0}^{2L} | ||
| Línea 119: | Línea 119: | ||
Y así no hemos cambiado nada en cuanto al formalismo del ''análisis de Fourier'', pero hemos adaptado la receta. | Y así no hemos cambiado nada en cuanto al formalismo del ''análisis de Fourier'', pero hemos adaptado la receta. | ||
Ya tenemos una nueva serie escrita en términos de nuestra nueva $x$ y tenemos la nueva receta para calcular los valores de $A$ en términos de nuestra nueva $x$ y en términos del nuevo periodo que ahora es $2L$ (ECNS $ | Ya tenemos una nueva serie escrita en términos de nuestra nueva $x$ y tenemos la nueva receta para calcular los valores de $A$ en términos de nuestra nueva $x$ y en términos del nuevo periodo que ahora es $2L$ (ECNS $9$, $12$, $13$). | ||
== Visualización para la Amplitud $A$. == | |||
Podemos pensar que nos podremos sumergir aún más en las matemáticas y comenzar a ejecutarlas, pero aún no lo voy a hacer. Primero, me gustaría echar un vistazo a los valores de $A$ (que ya estamos de acuerdo en que $A_{0}=0$), así que eso ya no es un problema, pero, por ejemplo, | Podemos pensar que nos podremos sumergir aún más en las matemáticas y comenzar a ejecutarlas, pero aún no lo voy a hacer. Primero, me gustaría echar un vistazo a los valores de $A$ (que ya estamos de acuerdo en que $A_{0}=0$), así que eso ya no es un problema, pero, por ejemplo, | ||
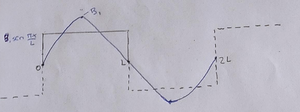
[[Archivo:Cuerda3.png|miniaturadeimagen|centro|La función (roja) $A_{1} \cos(\pi x/L)$, que sería el primer término de la serie del coseno y el segundo término sería 2 veces el $\cos(2\pi x/L)$]] | [[Archivo:Cuerda3.png|miniaturadeimagen|centro|Figura 5:La función (roja) $A_{1} \cos(\pi x/L)$, que sería el primer término de la serie del coseno y el segundo término sería 2 veces el $\cos(2\pi x/L)$]] | ||
Supongamos que encontramos el valor de $A_{1}$, pero eso es inaceptable ¿por qué es inaceptable? Miremos la función (cuadrada) y luego miremos la curva roja que es mi función | Supongamos que encontramos el valor de $A_{1}$ (Figura 5), pero eso es inaceptable ¿por qué es inaceptable? Miremos la función (cuadrada) y luego miremos la curva roja que es mi función | ||
$A_{1}$, se supone que la curva roja ayuda a construir la función cuadrada (gráfica | $A_{1}$, se supone que la curva roja ayuda a construir la función cuadrada (gráfica | ||
cuadrada), por lo que $A_{1}$, fuera de la pregunta, nunca puede contribuir a mi función (grafica cuadrada), pero no solo $A_{1}$ no puede contribuir, sino que cualquier función de | cuadrada), por lo que $A_{1}$, fuera de la pregunta, nunca puede contribuir a mi función (grafica cuadrada), pero no solo $A_{1}$ '''no''' puede contribuir, sino que cualquier función de | ||
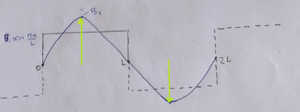
[[Archivo:Cuerda3.1.2.png| | [[Archivo:Cuerda3.1.2.png|miniaturadeimagen|derecha|Figura 6.]] | ||
$coseno$ que dibuje siempre será positiva en ambos lados (COLOR ANARANJADO), y exigiré que tenga que ser positiva arriba y, negativa debajo de cero, de lo contrario nunca podré construir esta función. | $coseno$ que dibuje siempre será positiva en ambos lados (COLOR ANARANJADO de la Figura 6), y exigiré que tenga que ser positiva arriba y, negativa debajo de cero, de lo contrario nunca podré construir esta función. | ||
Para ponerla de una manera más elegante, una función $coseno$ es una función par, lo que significa que | Para ponerla de una manera más elegante, una función $coseno$ es una función par, lo que significa que | ||
| Línea 141: | Línea 142: | ||
Para decirlo en pocas palabras, nunca se puede ajustar una función impar con funciones pares en Fourier, ni tampoco se puede ajustar una función par con funciones impares, por lo que quizás sea una mejor manera de verlo. | Para decirlo en pocas palabras, nunca se puede ajustar una función impar con funciones pares en Fourier, ni tampoco se puede ajustar una función par con funciones impares, por lo que quizás sea una mejor manera de verlo. | ||
== Visualización para la Amplitud $B$. == | |||
Ahora, echemos un vistazo a los valores para $B$, así que tengamos en cuenta que para $B$ las funciones serán sinusoidales, por lo que $A_{0}=0$, todos los valores para $A$ son $0$. Pasemos a los valores de $B$, así que voy a dibujar la función nuevamente. | Ahora, echemos un vistazo a los valores para $B$, así que tengamos en cuenta que para $B$ las funciones serán sinusoidales, por lo que $A_{0}=0$, todos los valores para $A$ son $0$. Pasemos a los valores de $B$, así que voy a dibujar la función nuevamente. | ||
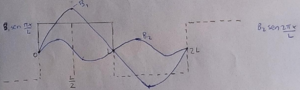
[[Archivo:Cuerda4.png|miniaturadeimagen|centro|$B_{1} sin(\pi x/L)$]] | [[Archivo:Cuerda4.png|miniaturadeimagen|centro|Figura 7:$B_{1} sin(\pi x/L)$]] | ||
Este $B_{1}$ es el primero en la serie de $B's$, que es lo que queremos exactamente, que esta función sinusoidal que tiene una la amplitud $B_{1}$, no podría ser mejor porque hay una montaña y un valle ( | Este $B_{1}$ (Figura 7) es el primero en la serie de $B's$, que es lo que queremos exactamente, que esta función sinusoidal que tiene una la amplitud $B_{1}$, no podría ser mejor porque hay una montaña y un valle (FLECHAS VERDES de la Figura 8). | ||
[[Archivo:Cuerda4.1.png|miniaturadeimagen|izquierda]] | [[Archivo:Cuerda4.1.png|miniaturadeimagen|izquierda|Figura 8.]] | ||
No es de extrañar porque la función asignada es una función impar y nuestra función es impar, así que claramente las funciones impares lo harán muy bien. | No es de extrañar porque la función asignada es una función impar y nuestra función es impar, así que claramente las funciones impares lo harán muy bien. | ||
Echemos ahora un vistazo a $B_{2}$ en la misma gráfica | Echemos ahora un vistazo a $B_{2}$ en la misma gráfica | ||
[[Archivo:Cuerda4.2.png|miniaturadeimagen|centro|$B_{2} sin(2\pi x/L)$]] | [[Archivo:Cuerda4.2.png|miniaturadeimagen|centro|Figura 9:$B_{2} sin(2\pi x/L)$]] | ||
No hay forma de que $B_{2}$ pueda hacerme algún bien, ¿por qué? | No hay forma de que $B_{2}$ pueda hacerme algún bien, ¿por qué? | ||
Una forma de verlo es que todo tiene que ser simétrico con respecto a la línea $L | Una forma de verlo es que todo tiene que ser simétrico con respecto a la línea $\frac{L}{2}$ si $B_{2}$ se va para arriba, la otra parte también tiene que irse para arriba y no está haciendo eso. | ||
Por lo tanto, podemos concluir que $B_{2}$ debe convertirse en $0$ y, por analogía, todos los valores pares de $m$ serán $0$, esta es una predicción que hago. No hemos hecho ningún ''análisis de Fourier'' elegante. Ya hemos concluido que, para nuestra función específica, para nuestra cuerda específica que se fija en ambos extremos, todos los valores para $A$ serán $0$ y que sólo los valores impares para $B$, para los cuales el valor $m$ es impar, obtendremos respuestas que no sean $0$. | Por lo tanto, podemos concluir que $B_{2}$ debe convertirse en $0$ y, por analogía, todos los valores pares de $m$ serán $0$, esta es una predicción que hago. No hemos hecho ningún ''análisis de Fourier'' elegante. Ya hemos concluido que, para nuestra función específica, para nuestra cuerda específica que se fija en ambos extremos, todos los valores para $A$ serán $0$ y que sólo los valores impares para $B$, para los cuales el valor $m$ es impar, obtendremos respuestas que no sean $0$. | ||
| Línea 159: | Línea 162: | ||
¡Redoble de tambores! Ya estamos listos para ejecutar la ''receta'' de Fourier (si quieres puedes hacer todas las $A's$ y verás que todas son $0$, lo dejo a disposición de los lectores que lo vean y quieran hacerlo), pero seguro que haré las $B´s$. | ¡Redoble de tambores! Ya estamos listos para ejecutar la ''receta'' de Fourier (si quieres puedes hacer todas las $A's$ y verás que todas son $0$, lo dejo a disposición de los lectores que lo vean y quieran hacerlo), pero seguro que haré las $B´s$. | ||
Ahora ejecutamos nuestra ''receta'' y de ( | Ahora ejecutamos nuestra ''receta'' y de $(13)$, obtendremos esa $B_{m}$ | ||
\begin{equation} | \begin{equation} | ||
B_{m}=\underbrace{\frac{A}{L} \int_{0}^{L} \sin \left( \frac{m \pi x}{L} \right) dx}_{ | B_{m}=\underbrace{\frac{A}{L} \int_{0}^{L} \sin \left( \frac{m \pi x}{L} \right) dx}_{16a} - \underbrace{\frac{A}{L} \int_{0}^{2L} \sin \left( \frac{m \pi x}{L} \right) dx}_{16b} | ||
\end{equation} | \end{equation} | ||
Hay ''análisis de Fourier'' cuando la función viene en más de dos partes, este es un caso fácil, por eso lo elegí. Esta integral $( | Hay ''análisis de Fourier'' cuando la función viene en más de dos partes, este es un caso fácil, por eso lo elegí. Esta integral $(16)$ es trivial, por supuesto, si hacemos la integral, obtenemos | ||
\begin{equation} | \begin{equation} | ||
\underbrace{ -\left[ \frac{A L}{L m \pi} \cos \left( \frac{m \pi x}{L} \right) \right]_{0}^{L}}_{ | \underbrace{ -\left[ \frac{A L}{L m \pi} \cos \left( \frac{m \pi x}{L} \right) \right]_{0}^{L}}_{17a} + \underbrace{\left[ \frac{A L}{L m \pi} \cos \left( \frac{m \pi x}{L} \right) \right]_{0}^{2L}}_{17b} | ||
\end{equation} | \end{equation} | ||
Cuando $m$ es impar, $( | Cuando $m$ es impar, $(17a)=-2$ ; $(17b)=2$. | ||
pero si $m$ es par, $ ( | pero si $m$ es par, $ (17a)=0=(17b) $. | ||
Por lo tanto, lo que sale es exactamente lo que predijimos: todos los valores pares de $m$ darán valores $0$ para $B$ y que sólo los valores impares me darán valores que no son $0$. | Por lo tanto, lo que sale es exactamente lo que predijimos: todos los valores pares de $m$ darán valores $0$ para $B$ y que sólo los valores impares me darán valores que no son $0$. | ||
Antes de escribir esto en una forma completa de Fourier, debe apreciar el hecho de que esta integral de $( | Antes de escribir esto en una forma completa de Fourier, debe apreciar el hecho de que esta integral de $(16a)$ me da exactamente la misma respuesta que esta integral $(16b)$. | ||
Siempre se da el caso que cuando se tiene una cuerda que está fija en ambos extremos y la integral de $0$ a $L$ siempre da la misma respuesta que la integral de $L$ a $2L$ que se introdujo para hacer la función periódica. | Siempre se da el caso que cuando se tiene una cuerda que está fija en ambos extremos y la integral de $0$ a $L$ siempre da la misma respuesta que la integral de $L$ a $2L$ que se introdujo para hacer la función periódica. | ||
Es por eso y sólo por esa razón que en libro de ''Anthony French''<ref>A.P.French. Vibrations and Waves, 3rd edition,Cap 6, 1970.</ref> da una forma mucho más fácil de calcular las componentes de Fourier en cuerdas y dice que todo lo que tienes que hacer es decir que $B_{m}$ es $\frac{2}{L}$, multiplicó nuestra ''receta'' por $2$, así que en lugar de tener$\frac{1}{L}$, dice que no, realmente deberíamos tener | Es por eso y sólo por esa razón que en libro de ''Anthony French''<ref>A.P.French. Vibrations and Waves, 3rd edition,Cap 6, 1970.</ref> da una forma mucho más fácil de calcular las componentes de Fourier en cuerdas y dice que todo lo que tienes que hacer es decir que $B_{m}$ es $\frac{2}{L}$, multiplicó nuestra ''receta'' por $2$, así que en lugar de tener$\frac{1}{L}$, dice que no, realmente deberíamos tener | ||
\begin{equation} | \begin{equation} | ||
| Línea 184: | Línea 188: | ||
Esta es la ecuación $(6.32)$ del libro de French, si eso es todo lo que supiéramos sobre el ''análisis de Fourier'', tendríamos una imagen muy estrecha de porqué es un caso extremadamente especial, pero es cierto que siempre que tengamos una cuerda que esté fija en ambos extremos, esto servirá. | Esta es la ecuación $(6.32)$ del libro de French, si eso es todo lo que supiéramos sobre el ''análisis de Fourier'', tendríamos una imagen muy estrecha de porqué es un caso extremadamente especial, pero es cierto que siempre que tengamos una cuerda que esté fija en ambos extremos, esto servirá. | ||
Sentí la obligación de mostrarles el formalismo de Fourier, por lo que ahora estamos listos para escribir la serie completa de Fourier, hay que observar que la suma de $( | == Serie completa de Fourier. == | ||
Sentí la obligación de mostrarles el formalismo de Fourier, por lo que ahora estamos listos para escribir la serie completa de Fourier, hay que observar que la suma de $(17)$ se convierte en | |||
\begin{equation} | \begin{equation} | ||
B_{m}=4\frac{A}{m \pi} | B_{m}=4\frac{A}{m \pi} | ||
| Línea 191: | Línea 196: | ||
pero $m$ es solo impar y, con eso en mente, puedo escribir la función, que fue uno de nuestros grandes pasos, en $t=0$, se puede escribir | pero $m$ es solo impar y, con eso en mente, puedo escribir la función, que fue uno de nuestros grandes pasos, en $t=0$, se puede escribir | ||
\begin{equation} | \begin{equation} | ||
y(x,0)=4\frac{A}{m \pi} \left[ \sin\left( \frac{\pi x}{L} \right) + \frac{1}{3} \sin\left( \frac{3 \pi x}{L}\right) + \frac{1}{5}\sin\left( \frac{5 \pi x}{L}\right) + ... \right] | \boxed{ y(x,0)=4\frac{A}{m \pi} \left[ \sin\left( \frac{\pi x}{L} \right) + \frac{1}{3} \sin\left( \frac{3 \pi x}{L}\right) + \frac{1}{5}\sin\left( \frac{5 \pi x}{L}\right) + ... \right] } | ||
\end{equation} | \end{equation} | ||
== Referencias. == | |||
[[categoría:Ondas]] | |||
[[Categoría: Investigación]] | |||
[[ | |||
[[ | |||
Revisión actual - 16:55 30 sep 2023
Jean-Baptiste Joseph Fourier.
Jean-Baptiste Joseph Fourier (Auxerre, Francia, 21 de marzo de 1768 - París, 16 de mayo de 1830), matemático y físico francés conocido por sus trabajos sobre la descomposición de funciones periódicas en series trigonométricas convergentes llamadas Series de Fourier, método con el cual consiguió resolver la ecuación del calor. La transformada de Fourier recibe su nombre en su honor. Fue el primero en dar una explicación científica al efecto invernadero en un tratado. En su honor un asteroide que fue descubierto en 1992 por el astrónomo belga Eric Walter Elst fue designado como Fourier .[1]
Formalismo General del Análisis de Fourier.
Supongamos que tenemos una cuerda de longitud L fija en sus dos extremos. Entonces, sabemos por lo que hemos aprendido, que comenzará a oscilar en un número infinito de modos normales, que son ondas estacionarias. Permitiendo la elección tanto de la amplitud como de fase de un modo dado, por lo que la pregunta de cien millones de pesos de hoy es: ¿en qué modos oscilará y cuáles son las amplitudes de esos modos si escribe y como una función de x y t?
La ecuación es: \begin{equation} y(x,t)= \sum_{n=1}^{\infty} B_{n} \sin(\kappa_{n}x) \cos(\omega_{n} t) \end{equation} donde $ \kappa_{n}=\frac{n \pi}{L} $ ; $ \omega_{n}=v \kappa_{n} $.
Sabemos que esto no es nada nuevo, así que también puedo mencionar que $t=0$ y puedo escribir esta forma en términos de una serie de senos,
\begin{equation}
t=0, \hspace{0.2cm} y(x,0)= B_{1} \sin(\frac{\pi x}{L})+ B_{2} \sin(\frac{2\pi x}{L})+ B_{3}...
\end{equation}
Y nuestra tarea es ver qué valores de n son necesarios para hacer ese pulso y cuáles son entonces las amplitudes B que tenemos aquí y de eso se trata el análisis de Fourier. Primero le daremos el enfoque general y luego, volveremos a este caso especial de una cuerda que se fija en ambos extremos, pero realmente creo que debemos ver el formato general. El procedimiento general, por lo que la idea detrás de Fourier es que cualquier función periódica, de valor único con un período de $2 \pi$ radianes, se puede representar mediante una serie de Fourier y escribiremos esta serie de Fourier, \begin{equation} f(x)= \underbrace{\frac{A_{0}}{2}}_{3a}+ \underbrace{\sum_{1}^{\infty} A_{m} \cos(mx)}_{3b}+ \underbrace{\sum_{1}^{\infty} B_{m} \sin(mx)}_{3c} \end{equation} Cabe resaltar que esta $x$ está en radianes.
Así que nuestra tarea ahora es encontrar los valores de $A$ y $B$ si conoce la función $ f(x) $ y construiremos la receta que nos permite calcular los valores de $A$ y los valores de $B$. Lo primero que hacemos para encontrar $A_{0}$ es tomar la integral $ \int_{-\pi}^{\pi} $ y veremos que para $(3b)$ y $(3c)$ son cero.
Por lo que nos queda de la siguiente forma el primer término de $(3)$ \begin{equation} \int_{-\pi}^{\pi} f(x)dx= \int_{-\pi}^{\pi} \frac{A_{0}}{2}dx =\pi A_{0} \end{equation} Si utilizo este resultado no es más que \begin{equation} \boxed{ A_{0}=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x)dx } \end{equation} Hay que tener en cuenta que $\frac{A_{0}}{2}$ no es más que el valor promedio de la función durante el periodo $2\pi$ y lo veremos más adelante. ¿Cómo vamos a calcular los otros valores para $A$? Lo que hacemos es tomar la integral, con los mismos intervalos que hace un momento, de $ \int_{-\pi}^{\pi} $ y veremos que para $(3a)$ y $(3c)$ son cero, también será cero para $(3b)$ excepto cuando $m=n$. Entonces, \[ \int_{-\pi}^{\pi} \cos(nx) dx \] Para $ n=1,2,3... $
Si nos fijamos en el término de $(3b)$, nos daremos cuenta que es $0$ excepto cuando $m=n$ (como lo mencionamos anteriormente). Cuando $m=n$, obtenemos \begin{equation} \int_{-\pi}^{\pi} \cos^{2}(mx)dx=\pi \end{equation} Así que ya tenemos una receta para $A_{m}$ que es \begin{equation} \boxed{ A_{m}= \int_{-\pi}^{\pi} f(x) \cos(mx) dx } \end{equation} Ya sabemos cómo calcular $A_{0}$ y sabemos cómo calcular los valores para $A_{m}$.
Ahora, encontraremos valores para $B$. Integraremos ambos lados de la integral entre $-\pi$ y $\pi$ multiplicado por el $\sin(nx)dx$ y cuando lo hagamos, veremos exactamente lo mismo que teníamos en $(3)$, veremos que $(3a)$ será $0$ al igual que $(3b)$, $(3c)$ siempre será $0$ excepto cuando $m=n$, entonces en $(3c)$ obtendremos el cuadrado del seno, y la integral del $\sin^{2}$ será $\pi$ casi igual que la integral $(6)$. Entonces, vemos que también tenemos la receta para encontrar todos los valores de $B_{m}$ \begin{equation} \boxed{ B_{m}= \int_{-\pi}^{\pi} f(x) \sin(mx) dx } \end{equation}
Podemos ver, en su forma más general, el formalismo del análisis de Fourier.
Hay que tener en cuenta que siempre que tengamos una integral de $-\pi$ a $\pi$, le podemos cambiar lo límites de integración, si se prefiere, de $0$ a $2\pi $, porque la función es periódica.
Si observamos estas tres recetas: $(5),(7),(8)$, podemos eliminar $(5)$ porque si hacemos que $m=0$ en $(7)$ ($m$ va de $1,2,3,4,5$), si también incluimos $m=0$ en $(7)$, obtendremos exactamente lo mismo que tenemos en $(5)$ porque cuando $m=0$, el coseno es uno, entonces $(5)$ y $(7)$ son idénticos.
Esa es la única razón por la que llamamos al término $(3a)$ constante que es $\frac{A_{0}}{2}$, podríamos haberlo llamado $C$ porque después de todo una constante es una constante; esta constante es el valor promedio de la función, entonces necesitaríamos esta $C$ en $(5)$ y tendríamos $\frac{1}{2 \pi}$ y, por lo tanto, necesitaríamos 3 recetas para hacer el análisis de Fourier, mientras que si definimos esta constante como $\frac{A_{0}}{2}$, solo necesitamos 2, pero $\frac{A_{0}}{2}$ es una constante y es el valor promedio de la función sobre el periodo.
Todo esto nos puede parecer un poco opaco por ahora y espero que quede claro en este trabajo cuando pongamos a trabajar este análisis de Fourier.
Lo que hemos visto hasta aquí (y así es como quiero que lo veas), es simplemente una receta y cuando usemos esta receta, la ejecutamos y no siempre nos preguntamos por qué la receta es así, al contrario, usamos las recetas (una analogía en la cocina) para cocinar una deliciosa comida, agua y/o postres.
Análisis de Fourier para una cuerda pulsada.
Así que ahora me gustaría volver a la cuerda pulsada, pero primero quiero echarle un vistazo de cerca en el momento $t=0$, y lo que voy a hacer es puntearla de una manera muy inusual. Hay una razón por la cual lo hago de manera tan inusual, porque es factible hacer el análisis de Fourier, así que ahora tengo una cuerda que está fija entre $0$ y $L$ y la voy a acoplar de una manera extraña, es decir,
Lo estoy forzando a un cuadrado para la cuerda, si quiero usar el análisis de Fourier y verán cómo lo voy a hacer porque necesito una función periódica y la que aparece en la imagen de aquí arriba no es periódica, así que la haré periódica. La forma para hacerla periódica es la siguiente: supongo que la función es realmente así,
Agregué esto: llegué a $2L$ pero voy mucho más allá, así que lo vuelvo a definir entre $0$ y $2L$ y eso ya periódico. Hay que notar que el patrón hacia arriba y hacia abajo es periódico, por lo que significa que mi periodo es $2L$ y al hacerlo, vemos que $\frac{A_{0}}{2}=0$ porque el valor promedio de esta función, que ahora está definido entre $0$ y $2 L$ y mucho más allá de $2L$ y por debajo de $0$, tiene un valor promedio de $0$ y, por lo tanto, mi función $f (x)$ puede escribirse como una función $y(x)$.
Ahora, quiero expresar esta forma en series de Fourier, pero antes de poder hacer eso, tengo que hacer algunos cambios en nuestra receta porque en la receta tenemos radianes en $(3)$ y los radianes son manzanas y en la imagen con la función periódica (Figura 4) tenemos $x$, pero no está en radianes, es decir, metros y los metros son peras.
Dicho esto, los radianes son manzanas y los metros son peras, pero ¿qué debo hacer para convertir las peras en manzanas? Tengo que tomar la antigua $x$ que estaba en radianes, que es la que tengo en (6) y esa es la que tengo en $(3b)$, voy a reemplazar eso en ese formalismo de la vieja $ x (radianes) \Rightarrow \frac{x \pi}{L}(metros) $.
Y esta última $x$ ya está en $metros^{-1}$. Podemos ver que, si mi $x$ ahora se convierte en $2L$, entonces esto se ha movido a $\pi$ radianes.
Con todo esto, ya podemos manejarlo de la misma manera porque ya tenemos manzanas en la imagen con función periódica y tenemos manzanas en las demás ecuaciones, eso significa que ahora mi serie de Fourier se va a parecer mucho a lo que tenemos en $(3)$, pero prefiero escribirlo nuevamente, nos queda \begin{equation} \boxed{ y(x)=f(x)=\frac{A_{0}}{2}+ \sum_{1}^{\infty}A_{m} \cos \left(\frac{m \pi x}{L}\right)+ \sum_{1}^{\infty}B_{m} \sin \left(\frac{m \pi x}{L}\right) } \end{equation} Hemos hecho una modificación a la idea general que está en radianes $(3)$ para que sea aplicable a un caso en el que no tenemos radianes. Antes de que podamos ejecutar el análisis de Fourier, también tengo que cambiar la receta en términos de $A_{m}$ y $B_{m}$.
En primer lugar, no tengo una integral durante un periodo de $2\pi$, pero tengo que hacer una integral de $0$ a $2L$ o de $-L$ a $L$, por lo que antes tenía \begin{equation} \frac{1}{\pi} \int_{-\pi}^{\pi} \hspace{0.3cm}; \int_{0}^{2L} \hspace{0.3cm}; \int_{-L}^{L} \end{equation} Lo podemos expresar como cualquiera de las integrales de $(10)$.
Tengo que cambiar este $\frac{1}{\pi}$ que tenemos al frente de $(10)$ porque eso fue el resultado de la integral $(6)$ y si hacemos la integral, habremos encontrado $L$ y no $\pi$, esto es la mitad del periodo y la mitad del periodo de nuestra función es $L$, por lo que debe cambiarse a \begin{equation} \frac{1}{\pi} \rightarrow \frac{1}{L} \int_{0}^{2L} \end{equation}
Y, por lo tanto, para asegurarme de que no se confunda, voy a reescribir la receta de la siguiente manera \begin{equation} \boxed{ A_{m}=\frac{1}{L} \int_{0}^{2L} f(x) \cos \left( \frac{m \pi x}{L} \right) dx } \end{equation} Y $B_{m}$ es entonces \begin{equation} \boxed{ B_{m}=\frac{1}{L} \int_{0}^{2L} f(x) \sin \left( \frac{m \pi x}{L} \right) dx } \end{equation} Y así no hemos cambiado nada en cuanto al formalismo del análisis de Fourier, pero hemos adaptado la receta.
Ya tenemos una nueva serie escrita en términos de nuestra nueva $x$ y tenemos la nueva receta para calcular los valores de $A$ en términos de nuestra nueva $x$ y en términos del nuevo periodo que ahora es $2L$ (ECNS $9$, $12$, $13$).
Visualización para la Amplitud $A$.
Podemos pensar que nos podremos sumergir aún más en las matemáticas y comenzar a ejecutarlas, pero aún no lo voy a hacer. Primero, me gustaría echar un vistazo a los valores de $A$ (que ya estamos de acuerdo en que $A_{0}=0$), así que eso ya no es un problema, pero, por ejemplo,
Supongamos que encontramos el valor de $A_{1}$ (Figura 5), pero eso es inaceptable ¿por qué es inaceptable? Miremos la función (cuadrada) y luego miremos la curva roja que es mi función $A_{1}$, se supone que la curva roja ayuda a construir la función cuadrada (gráfica cuadrada), por lo que $A_{1}$, fuera de la pregunta, nunca puede contribuir a mi función (grafica cuadrada), pero no solo $A_{1}$ no puede contribuir, sino que cualquier función de
$coseno$ que dibuje siempre será positiva en ambos lados (COLOR ANARANJADO de la Figura 6), y exigiré que tenga que ser positiva arriba y, negativa debajo de cero, de lo contrario nunca podré construir esta función.
Para ponerla de una manera más elegante, una función $coseno$ es una función par, lo que significa que \begin{equation} f(x)=f(-x) \end{equation}
Pero nuestra función, de la forma en que la definimos, es impar y una función impar \begin{equation} f(x)=-f(-x) \end{equation}
Para decirlo en pocas palabras, nunca se puede ajustar una función impar con funciones pares en Fourier, ni tampoco se puede ajustar una función par con funciones impares, por lo que quizás sea una mejor manera de verlo.
Visualización para la Amplitud $B$.
Ahora, echemos un vistazo a los valores para $B$, así que tengamos en cuenta que para $B$ las funciones serán sinusoidales, por lo que $A_{0}=0$, todos los valores para $A$ son $0$. Pasemos a los valores de $B$, así que voy a dibujar la función nuevamente.
Este $B_{1}$ (Figura 7) es el primero en la serie de $B's$, que es lo que queremos exactamente, que esta función sinusoidal que tiene una la amplitud $B_{1}$, no podría ser mejor porque hay una montaña y un valle (FLECHAS VERDES de la Figura 8).
No es de extrañar porque la función asignada es una función impar y nuestra función es impar, así que claramente las funciones impares lo harán muy bien.
Echemos ahora un vistazo a $B_{2}$ en la misma gráfica
No hay forma de que $B_{2}$ pueda hacerme algún bien, ¿por qué?
Una forma de verlo es que todo tiene que ser simétrico con respecto a la línea $\frac{L}{2}$ si $B_{2}$ se va para arriba, la otra parte también tiene que irse para arriba y no está haciendo eso.
Por lo tanto, podemos concluir que $B_{2}$ debe convertirse en $0$ y, por analogía, todos los valores pares de $m$ serán $0$, esta es una predicción que hago. No hemos hecho ningún análisis de Fourier elegante. Ya hemos concluido que, para nuestra función específica, para nuestra cuerda específica que se fija en ambos extremos, todos los valores para $A$ serán $0$ y que sólo los valores impares para $B$, para los cuales el valor $m$ es impar, obtendremos respuestas que no sean $0$.
¡Redoble de tambores! Ya estamos listos para ejecutar la receta de Fourier (si quieres puedes hacer todas las $A's$ y verás que todas son $0$, lo dejo a disposición de los lectores que lo vean y quieran hacerlo), pero seguro que haré las $B´s$.
Ahora ejecutamos nuestra receta y de $(13)$, obtendremos esa $B_{m}$ \begin{equation} B_{m}=\underbrace{\frac{A}{L} \int_{0}^{L} \sin \left( \frac{m \pi x}{L} \right) dx}_{16a} - \underbrace{\frac{A}{L} \int_{0}^{2L} \sin \left( \frac{m \pi x}{L} \right) dx}_{16b} \end{equation}
Hay análisis de Fourier cuando la función viene en más de dos partes, este es un caso fácil, por eso lo elegí. Esta integral $(16)$ es trivial, por supuesto, si hacemos la integral, obtenemos \begin{equation} \underbrace{ -\left[ \frac{A L}{L m \pi} \cos \left( \frac{m \pi x}{L} \right) \right]_{0}^{L}}_{17a} + \underbrace{\left[ \frac{A L}{L m \pi} \cos \left( \frac{m \pi x}{L} \right) \right]_{0}^{2L}}_{17b} \end{equation}
Cuando $m$ es impar, $(17a)=-2$ ; $(17b)=2$.
pero si $m$ es par, $ (17a)=0=(17b) $.
Por lo tanto, lo que sale es exactamente lo que predijimos: todos los valores pares de $m$ darán valores $0$ para $B$ y que sólo los valores impares me darán valores que no son $0$.
Antes de escribir esto en una forma completa de Fourier, debe apreciar el hecho de que esta integral de $(16a)$ me da exactamente la misma respuesta que esta integral $(16b)$. Siempre se da el caso que cuando se tiene una cuerda que está fija en ambos extremos y la integral de $0$ a $L$ siempre da la misma respuesta que la integral de $L$ a $2L$ que se introdujo para hacer la función periódica.
Es por eso y sólo por esa razón que en libro de Anthony French[2] da una forma mucho más fácil de calcular las componentes de Fourier en cuerdas y dice que todo lo que tienes que hacer es decir que $B_{m}$ es $\frac{2}{L}$, multiplicó nuestra receta por $2$, así que en lugar de tener$\frac{1}{L}$, dice que no, realmente deberíamos tener \begin{equation} B_{m}=\frac{2}{L} \int_{0}^{L} f(x) \sin \left( \frac{m \pi x}{L} \right) dx \end{equation}
Esta es la ecuación $(6.32)$ del libro de French, si eso es todo lo que supiéramos sobre el análisis de Fourier, tendríamos una imagen muy estrecha de porqué es un caso extremadamente especial, pero es cierto que siempre que tengamos una cuerda que esté fija en ambos extremos, esto servirá.
Serie completa de Fourier.
Sentí la obligación de mostrarles el formalismo de Fourier, por lo que ahora estamos listos para escribir la serie completa de Fourier, hay que observar que la suma de $(17)$ se convierte en \begin{equation} B_{m}=4\frac{A}{m \pi} \end{equation}
pero $m$ es solo impar y, con eso en mente, puedo escribir la función, que fue uno de nuestros grandes pasos, en $t=0$, se puede escribir \begin{equation} \boxed{ y(x,0)=4\frac{A}{m \pi} \left[ \sin\left( \frac{\pi x}{L} \right) + \frac{1}{3} \sin\left( \frac{3 \pi x}{L}\right) + \frac{1}{5}\sin\left( \frac{5 \pi x}{L}\right) + ... \right] } \end{equation}
Referencias.
- ↑ http://matematicos.matem.unam.mx/otras-efemerides-de-todo-el-mes-de-marzo/1270-21-de-marzo-natalicio-de-jean-baptiste-joseph-fourier
- ↑ A.P.French. Vibrations and Waves, 3rd edition,Cap 6, 1970.