Vibraciones en estructuras
Introducción
El estudio de las vibraciones en estructuras es de vital importancia para garantizar la seguridad de una edificación, este tipo de análisis comenzó a tomarse en serio cuando ocurrió un terremoto en Santa Barbara , California y causo múltiples daños a las estructuras de la localidad. Una de las razones principales de lo ocurrido fue que al realizar los cálculos para las cargas con las que interactúa la estructura nunca se considero una carga generada por un terremoto, en otras palabras, no se considero un análisis dinámico de la estructura.
Cuando se consideran problemas más realistas como los que involucran fuerzas de fricción debidas a superficies o debidas a un medio viscoso es frecuente que no se logre una solución analítica de problema sin embargo es posible una solución numérica que permitirá una conocer un comportamiento aproximado del problema. Existen numerosos métodos numéricos para distintos propósitos , un ejemplo de ello son los métodos para determinar integrales definidas (regla de Simpson y método del trapecio). Para brindar una solución numérica a las ecuaciones que involucran un análisis dinámico se requiere el método conocido como elemento finito o el método de diferencias finitas. En el presente escrito se utilizará el método se empleara el método del elemento finito para realizar un estudio de las vibraciones en estructuras.
Cuando se comenzó el desarrollo del análisis vibracional en estructuras y comenzó el uso de los métodos numéricos, los ingenieros estructuristas se percataron de lo complicado que pueden tornarse los cálculos por la gran cantidad de valores numéricos que se manejan. Este inconveniente dio pie al desarrollo de software especializado para poder facilitar los cálculos y posteriormente permitir una visualización y simulación computarizada de la estructura.
En la actualidad existen numeras empresas que ofrecen software para diseño mecánico y su posterior análisis.Un ejemplo de esto es el software ANSYS.
Par comenzar con el estudio se planteará primeramente un problema que involucra una vibración con varios grados de libertad y las ecuaciones involucradas en este problema, el propósito de esto tiene la finalidad de hacer una introducción a la notación y los objetos matemáticos empleados a lo largo del escrito.
Una vez familiarizados con la notación se procede a realizar un análisis a la ecuaciones de Lagrange, las cuales se emplearán en el planteamiento de la formulación de elemento finito para miembros axiales , conociendo esta formulación resulta inmediata la formulación para vigas y marcos.
Múltiples grados de libertad.
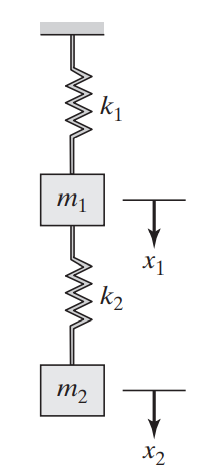
Como se explico anteriormente , el propósito de este primer apartado es hacer una introducción a la notación a emplear y a los métodos matemáticos involucrados. Consideremos la imagen mostrada a continuación.
De la imagen anterior y considerando un desplazamiento con la condición $ x_2 > x_1 $ , tenemos lo siguiente.
$ m_1 \ddot{x_1} + 2kx_1 -kx_2 = 0$
$ m_2 \ddot{x_2} -kx_1 + 2kx_2 = 0$
En forma matricial las ecuaciones anteriores se escriben de la forma expresada a continuación.
$ \left(\begin{smallmatrix} m_1 & 0 \\ 0 & m_2 \\ \end{smallmatrix}\right) $ $ \left(\begin{smallmatrix} \ddot{x_1} \\ \ddot{x_2} \\ \end{smallmatrix}\right) $ + $ \left(\begin{smallmatrix} 2k & -k \\ -k & 2k\\ \end{smallmatrix}\right) $ $ \left(\begin{smallmatrix} x_1 \\ x_2 \\ \end{smallmatrix}\right) $ = $ \left(\begin{smallmatrix} 0 \\ 0 \\ \end{smallmatrix}\right) $
La expresión anterior adquiere una forma mas compacta de la forma siguiente:
$[M] [\ddot{x} ] + [K][x]=0$
Debe notarse que el sistema de ecuaciones diferencias esta acoplado , es decir abas ecuaciones incluyen las variables $ x_1 , x_2$. Se procede a dividir el sistema de ecuaciones entre $ m_1$ y $m_2$ respectivamente para obtener la forma siguiente:
$[\ddot{x}] + [M]^{-1} [K][x] = 0$
A continuación se asumen soluciones de la forma $ x_1(t) = X_1 Cos(\omega t + \phi)$ y $ x_2(t) = X_2 Cos(\omega t + \phi)$ , o para expresar lo anterior de forma mas reducida se usa una forma matricial como la mostrada a continuación:
$[x] = [X] Sin(\omega t + \phi)$
Lo cual permite llegar al siguiente el resultado una ves simplificadas las funciones trigonométricas.
$-\omega^{2}$ $ \left(\begin{smallmatrix} X_1 \\ X_2 \\ \end{smallmatrix}\right) $ + $ \left(\begin{smallmatrix} 2k/m_1 & -k/m_1 \\ -k/m_2 & 2k/m_2 \\ \end{smallmatrix}\right) $ $ \left(\begin{smallmatrix} X_1 \\ X_2 \\ \end{smallmatrix}\right) $ = $ \left(\begin{smallmatrix} 0\\ 0 \\ \end{smallmatrix}\right) $
Reescribiendo la ecuación anterior obtenemos el resultado mostrado a continuación.
$ -\omega^{2}$ $ \left(\begin{smallmatrix} 1 & 0 \\ 0 & 1\\ \end{smallmatrix}\right) $ $ \left(\begin{smallmatrix} X_1\\ X_2\\ \end{smallmatrix}\right) $ + $ \left(\begin{smallmatrix} 1/m_1 & 0 \\ 0 & 1/m_2\\ \end{smallmatrix}\right) $ $ \left(\begin{smallmatrix} 2k & -k \\ -k & 2k\\ \end{smallmatrix}\right) $ $ \left(\begin{smallmatrix} X_1\\ X_2 \\ \end{smallmatrix}\right) $ = $ \left(\begin{smallmatrix} 0\\ 0\\ \end{smallmatrix}\right) $
Agrupando términos se llega al siguiente resultado.
$[ \left(\begin{smallmatrix} 2k/m_1 & -k/m_1 \\ -k/m_2 & 2k/m_2 \\ \end{smallmatrix}\right) $ $-\omega^{2}$ $ \left(\begin{smallmatrix} 1 & 0 \\ 0 & 1\\ \end{smallmatrix}\right)] $ $ \left(\begin{smallmatrix} X_1\\ X_2\\ \end{smallmatrix}\right) $ = $ \left(\begin{smallmatrix} 0\\ 0\\ \end{smallmatrix}\right) $
Realizando la operación entre matrices tenemos el resultado buscado.
$[ \left(\begin{smallmatrix} -\omega^{2} + 2k/m_1 & -k/m_1 \\ -k/m_2 & -\omega^{2} + 2k/m_2 \\ \end{smallmatrix}\right)] $ $ \left(\begin{smallmatrix} X_1\\ X_2\\ \end{smallmatrix}\right) $ = $ \left(\begin{smallmatrix} 0\\ 0\\ \end{smallmatrix}\right) $
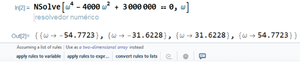
La expresión anterior tiene solución no trivial si y solo si el determinante de la matriz es cero, asignamos valores numéricos para poder obtener las frecuencias naturales haciendo $m_1 = m_2 = 0.1 kg$ y ,$k = 100 N/m$ obtenemos la siguiente ecuación.
$ \omega^{4} - 4000\omega^{2} + 3,000,000 = 0$
Se procede a resolver la ecuación anterior con Wolfram Mathemathica y se muestran las frecuencias naturales de oscilación, el conocer estas frecuencias en una estructura permitirá poder prever el movimiento al que están sujetas ciertas partes de la estructura y por lo tanto se podrán diseñar disipadores estructurales para un optimo funcionamiento de la edificación.
Ecuaciones de Lagrange
A continuación se emplearán las ecuaciones de Lagrange para poder obtener expresiones similares a las obtenidas anteriormente y mostrar así la equivalencia entre las ecuaciones de Newton y las ecuaciones de Lagrange.
Del diagrama anterior se obtienen las expresiones para la energía cinética y potencial,
$\mathcal{E}_{\mathrm{kin}} = 1/2 m_1 \dot{x_1}^{2} + 1/2 m_2 \dot{x_2}^{2},$
$\mathcal{V}_{\mathrm{pot}}= 1/2 k_1 x_1^{2} + 1/2 k_2 (x_2 - x_1)^{2}.$
Las ecuaciones de Lagrange para los dos grados de libertad son las siguientes:
$ \frac{d}{dt} \frac{\partial L}{\partial \dot{x_1}} - \frac{\partial L}{\partial x_1} = 0$
$ \frac{d}{dt} \frac{\partial L}{\partial \dot{x_2}} - \frac{\partial L}{\partial x_2} = 0$
$\frac{d}{dt} \frac{\partial L}{\partial \dot{x_1}} = m_1 \ddot{x_1}$
$\frac{d}{dt} \frac{\partial L}{\partial \dot{x_2}} = m_2 \ddot{x_2}$
$\frac{\partial L}{\partial x_1} = k_1 + k_2(x_1 - x_2)$
$\frac{\partial L}{\partial x_2} = k_2(x_2 - x_1)$
Evaluando las expresiones anteriores en las ecuaciones de Lagrange , obtenemos el sistema de ecuaciones mostrando en seguida.
$m_1 \ddot{x_1} + (k_1 + k_2)x_1 - k_2 x_2 = 0$
$m_2 \ddot{x_2} - k_2x_1 + k_2 x_2 = 0$
Si se expresamos las ecuaciones anteriores en forma matricial se obtiene un resultado parecido al obtenido anteriormente.
$ \left(\begin{smallmatrix} m_1 & 0\\ 0 & m_2 \\ \end{smallmatrix}\right) $ $ \left(\begin{smallmatrix} \ddot{x_1}\\ \ddot{x_2}\\ \end{smallmatrix}\right) $ + $ \left(\begin{smallmatrix} k_1 + k_2 & -k_2\\ -k_2 & k_2 \\ \end{smallmatrix}\right) $ $ \left(\begin{smallmatrix} x_1\\ x_2 \\ \end{smallmatrix}\right) $ = $ \left(\begin{smallmatrix} 0\\ 0 \\ \end{smallmatrix}\right) $
Introducción histórica al elemento finito
De forma breve, el elemento finito es un método numérico que permite resolver ecuaciones diferenciales , el método se basa en la división sucesiva de un cuerpo o dominio sobre el que están definidas ciertas ecuaciones integrales que caracterizan un fenómeno físico en una serie de subdominios que o intersecan entre si denominados elementos finitos ,el conjunto de estos elementos forma una malla (discretización).
Algunos consideran que a Arquímedes fue una de las primeras personas en emplear un método de discretización para el cálculo de arreas y volúmenes.
En el año de 1941 Alexander Hrenikoff desarrollo una forma de abordar problemas elásticos el cual llevaba el nombre de "metodo de trabajo del marco".
Durante los años 1950 a 1962 M.J. Turner perfecciona el método de rigidez y esto permite el calculo de matrices de rigidez para vigas, armaduras y otros elementos R.W Clough fue el primero en acuñar el termino elemento finito.
Fundamentos matemáticos de la teoría de elementos finitos
Antes de adentrarnos en el elemento finito consideremos primeramente el método numérico de las diferencias finitas, en este método se prende sustituir las ecuaciones diferenciales(derivadas) por cocientes de diferencias , estas expresiones generan un sistema de ecuaciones considerando las condiciones de frontera del problema en cuestiones problema de este método radica en la herencia de la operación derivada , pues se presentan problemas al considerar geometrías irregulares. Frente a estas situación el elemento finito considera que cualquier función continua sobre el elemento considerado puede ser representada de forma lineal.
Explicación del método con un ejemplo de conducción de calor.
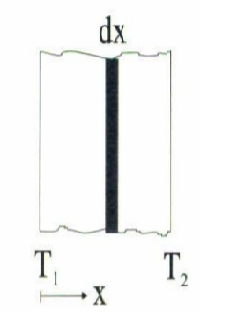
Desde un punto de vista macroscópico la transferencia de calor en un solido depende de las propiedades físicas del cuerpo ,su geometría y la diferencia de temperatura en el cuerpo considerado. Para analizar la conducción de calor consideremos una pared homogénea cuyos extremos tienen temperaturas constantes como se muestra a continuación en la imagen.
Si se considera que $ T_1 > T_2 $ entonces el flujo de calor es de izquierda a derecha. Si definimos a $q$ como la densidad de flujo de calor debida a una diferencia de temperatura o bien como la energía que atraviesa por unidad de tiempo una área unitaria perpendicular a la dirección del flujo de energía entonces por la relación de Fourier se establece la siguiente ecuación :
\[q =-k \frac{dT}{dx}\].
De la ecuación anterior $k$ es la conductividad térmica del material. El signo negativo en la ecuación indica que el flujo de energía es en el sentido en el que la temperatura disminuye con respecto a la distancia. Si se considera que la conductividad térmica es constante y además que $q$ es la misma en cada sección , podemos integrar la ecuación diferencial anterior y obtener el siguiente resultado.
\[T = -q/k x + const\]
Como se mencionó anteriormente las ecuaciones obtenidas deben estar sujetas a las condiciones del problema en general. Haciendo $ T(x = 0) = T_1$ , obtenemos la constante buscada y la solución particular al problema.
\[T_2 = -q/k L + T_1\]
o bien:
\[q=k/L (T_1 - T_-2) = k/L \delta T \]
Si reescribimos para un punto arbitrario encontramos que que la temperatura varia linealmente si el coeficiente de conductividad térmica es constante.
\[T(x) = T_1 - \frac{T_1 - T_2}{L}x\]
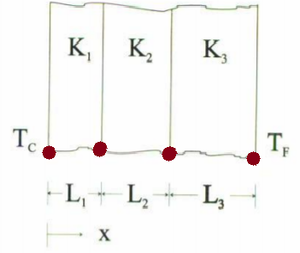
Consideremos ahora una división el material como se muestra a continuación donde cada sección tiene una conductividad térmica constante. Nótese que se tienen tres elementos finitos y 4 nodos.
Consideremos ahora la ecuación que describe las densidades de flujo de calor en los nodos 1 y 2.
\[ q_1^{e}= \frac{k^{e}}{L^{e}}(T_1^{e}-T_2^{e})\]
Debido a la conservación de la energía el flujo (salida) en el nodo 2 es de signo contrario a la entrada, por lo tanto escribimos la siguiente expresión que relaciona los nodos2 y 3.
\[ q_2^{e}= \frac{-k^{e}}{L^{e}}(T_1^{e}-T_2^{e})\]
De forma mas general tenemos el resultado mostrado a continuación.
\[[k^{e}][T^{e}]=[q^{e}]\]
Donde $[k^{e}]$ es la matriz de rigidez o de conductividad térmica. El nombre de rigidez proviene de un problema de mecánica estructural en la que fue empleando por primera vez el método de elemento finito.
Ahora procedemos a "enlazar" los nodos, es decir se construye la geometría del sistema , de esta forma se obtendrá una continuidad en el sistema , para este ejemplo las ecuaciones siguientes definen la continuidad.
\[T_1^{1} = T_1\] \[T_2^{1} = T_2 =T_1^{2}\] \[T_2^{2} = T_3 = T_1 ^{3}\] \[T_2^{3} = T_4\]
Para las conductividades se tiene las siguientes relaciones:
\[k^{1} = k_1\] \[k^{2} = k_2\] \[k^{3} = k_3\]
Para las longitudes se tienen las ecuaciones presentadas a continuación.
\[L^{1} = L_1\] \[L^{2} = L_2\] \[L^{3} = L_3\]
Se procede a calcular el flujo neto en cada nodo, considerando que para los nodos 2 y 3 el flujo neto es cero. Para el nodo 1: \[ q = \frac{k_1}{L_1}(T_1 - T_2)\]
Para el nodo 2: \[ 0 = \frac{k_2}{L_2}(T_2 - T_3) -\frac{k_1}{L_1}(T_1 - T_2) \]
Para el nodo 3: \[ 0 = \frac{k_3}{L_3}(T_3 - T_4) -\frac{k_3}{L_3}(T_4 - T_3) \]
Para el nodo 4: \[ q = \frac{-k_3}{L_3}(T_3 - T_4)\]
La expresiones anteriores pueden reescribirse en forma matricial.
$
\left(\begin{smallmatrix}
k_1/L_1 & -k_1/L_1 & 0 & 0\\
-k_1/L_1 & k_1/L1 + k_2/L_2 & -k_2/L_2 & 0\\
0 & -k_2/L_2 & k_2/L_2 + k_3/L_3 & -k_3/L_3\\
0 & 0 & -k_3/L_3 & k_3/L_3\\
\end{smallmatrix}\right)
$
$
\left(\begin{smallmatrix}
T_1\\
T_2\\
T_3\\
T_4\\
\end{smallmatrix}\right)
$
=
$
\left(\begin{smallmatrix}
q\\
0\\
0\\
-q\\
\end{smallmatrix}\right)
$
Este sistema no tendrá solución a menos que la matriz de rigidez sea invertible ,este problema se resuelve considerando sub-matrices y posteriormente se suman.
Matriz 1:
$\left(\begin{smallmatrix} k_1/L_1 & -k_1/L_1 & 0 & 0\\ -k_1/L_1 & k_1/L1 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ \end{smallmatrix}\right) $
Matriz 2:
$\left(\begin{smallmatrix} 0 & 0 & 0 & 0\\ 0 & k_2/L_2 & -k_2/L_2 & 0\\ 0 & -k_2/L_2 & k_2/L_2& 0\\ 0 & 0 & 0 & 0\\ \end{smallmatrix}\right) $
Matriz 3:
$\left(\begin{smallmatrix} 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & k_3/L_3& -k_3/L_3\\ 0 & 0 & -k_3/L_3& k_3/L_3\\ \end{smallmatrix}\right) $
Desde el punto de vista computacional esta ultima parte del procedimiento pone de manifiesto la necesidad de equipos de computo con mayor rendimiento.
Formulación de elemento finito para miembros axiales
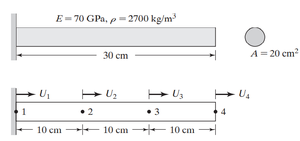
A continuación se emplean las ecuaciones de Lagrange para determinar la matriz de masa en un elemento axial y posteriormente se obtienen las frecuencias naturales para el mismo tipo de elemento. Debe recordarse que un miembro axial es aquel que solo puede presentar dos estados : compresión o tensión.
Se comienza por considerar que el desplazamiento uniaxial se expresa de la forma siguiente:
$u=S_i U_i + S_j U_j$
Donde cada función se expresa a continuación en función de la variable x ,la variable para el problema ilustrado en la imagen anterior.
$S_i = 1- x/L$
$S_j = x/L$
Se expresa la energía cinética del miembro como la suma de de las energías cinéticas de las partículas constitutivas.
\[T=
\int_{0}^{L} \! (\gamma /2 )\dot{u}^{2} \, dx
\]
En la expresión anterior $\gamma$ es la masa por unidad de longitud y $\dot{u} $es la velocidad de las partículas a lo largo del miembro. La velocidad $\dot{u}$ puede ser expresada como en términos de las velocidades nodales , es decir :
$\dot{u} = S_i \dot{U_i} + S_j \dot{U_j}$
Evaluando la expresión anterior en la integral para obtener la energía cinética tenemos lo siguiente.
\[T= \int_{0}^{L} \! (\gamma /2 ) (S_i \dot{U_i} + S_j \dot{U_j})^{2}\, dx \]
Aplicando las ecuaciones de Lagrange obtenemos lo siguiente.
\[ \frac{\partial T}{\partial \dot{U_i}} = (\gamma/2)\int_{0}^{L} \! 2S_i (S_i \dot{U_i} + S_j \dot{U_j})\, dx\] \[ \frac{\partial T}{\partial \dot{U_j}} = (\gamma/2)\int_{0}^{L} \! 2S_j (S_i \dot{U_i} + S_j \dot{U_j})\, dx\] \[ \frac{d}{dt} \frac{\partial T}{\partial \dot{U_i}} =\gamma \int_{0}^{L} \! S_i ^{2}\ddot{U_i} dx + \gamma \int_{0}^{L} \! S_i S_j\ddot{U_j} dx \] \[ \frac{d}{dt} \frac{\partial T}{\partial \dot{U_i}} =\gamma \int_{0}^{L} \! S_j ^{2}\ddot{U_j} dx + \gamma \int_{0}^{L} \! S_i S_j\ddot{U_i} dx \]
Recordando que $U_i$ y $U_j$ son funciones de x , tenemos los siguientes resultados.
\[ \gamma \int_{0}^{L} \! S_i ^{2} dx = \gamma \int_{0}^{L} \! (1-x/L)^{2} dx = \gamma L/3 \] \[ \gamma \int_{0}^{L} \! S_i S_j dx = \gamma \int_{0}^{L} \! (1-x/L)(x/L) dx = \gamma L/6 \] \[ \gamma \int_{0}^{L} \! S_j ^{2} dx = \gamma \int_{0}^{L} \! (x/L)^{2} dx = \gamma L/3 \]
Si se subsisten los resultados anteriores en las ecuaciones de Lagrange se puede notar que la matriz de masa tiene la forma siguiente:
\[ [M]^{e} = \gamma L/6 \left(\begin{smallmatrix} 2 & 1 \\ 1 & 2\\ \end{smallmatrix}\right) \]
Y la matriz de rigidez para miembros axiales tiene la forma siguiente:
\[ [K]^{e} = A E/L \left(\begin{smallmatrix} 1 & -1 \\ -1 & 1\\ \end{smallmatrix}\right) \]
Estas dos matrices se aplicarán al análisis de una viga circular empotrada en un extremo.
Evaluando los datos de la figura anterior tenemos lo siguiente:
\[ [K]^{1} = [K]^{2} = [K]^{3}= 1.4*10^ {9}\left(\begin{smallmatrix} 1 & -1 \\ -1 & 1\\ \end{smallmatrix}\right)\]
Realizando un arreglo a ambas matrices y considerando que nodo uno carece de movimiento por la condición de empotramiento obtenemos las siguiente matrices.
\[ [M]^{G} = \left(\begin{smallmatrix} 0.36 & 0.09 & 0\\ 0.09 & 0.36 & 0.09 \\ 0 & 0.09 & 0.18\\ \end{smallmatrix}\right)\]
\[[K]^{G} = 10^{9}\left(\begin{smallmatrix} 2.8 & -1.4 & 0\\ -1.4 & 2.8 & -1.4\\ 0 & -1.4 & 1.4\\ \end{smallmatrix}\right)\]
Se procede a invertir la matriz de masa y se multiplica por la matriz de rigidez, una vez realizado este se calculan los eigenvalores.A continuación se muestra una captura de pantalla del software Matlab que se empleó para realiza las operaciones entre matrices.
Si se calcula la raíz cuadrada de cada elemento del vector de eigenvalores se obtienen las siguientes frecuencias naturales de oscilación para la viga circular. \[\omega_1 = 1.599*10^5 rad/s\] \[\omega_2 =0.8819*10^5 rad/s \] \[\omega_3 = 0.2697*10^5 rad/s\]
Bibliografía
Moaveni, S. (2015). Finite element analysis (4th ed., pp. 629-666). Natick,MA: Pearson.
Aragón G. y Aragón J.(1998). Aspectos físicos y matemáticos del método del elemento finito.REVISTA MEXICANA DE FÍSICA 44(3),292-294.
Aportación por usuario: Alexjosemeza (discusión) 23:35 18 nov 2020 (CST)