Vibra: Oscilador de Duffing
Introducción
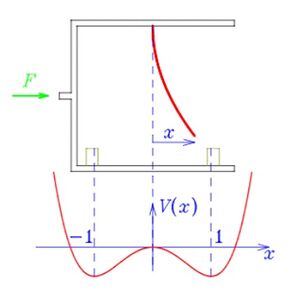
Podemos pensar qué modela el movimiento de una barra de acero cuando se coloca al centro de dos imanes equidistantes que la atraen, colocados a una distancia adecuada para que la barra no los toque. Los imanes generan un doble pozo de atracción, con un punto inestable en el centro al que consideramos el origen.
Consideraremos estudiar este sistema unidimensional no lineal en forma cualitativa, construyendo las soluciones en el espacio fase.
Consideremos primeramente un sistema unidimensional con una fuerza conservativa \[ F(x) = -\frac{dV(x)}{dx} \] Se sabe cualitativamente que las soluciones y en donde la fuerza se anula, se tienen puntos de equilibrio. En este caso se anulan en mínimos y máximos del potencial. Igualmente se sabe que la energía se conserva.
La energía mecánica, definida como la energía cinética más la energía potencial, debe ser constante \[ E = \frac{1}{2} m\dot{x}+V(x) = cte. \] Después podemos despejar a $\dot{x}$ \[ \dot{x}= \sqrt{\frac{2}{m}(E-V(x))} \] y separando variables tenemos \[ \int_{0}^{t} dt = \int_{x_{0}}^{x} \frac{dx}{\sqrt{\frac{2}{m}(E-V(x))}} \]
Podríamos decir que se tiene una solución de manera integral, pero en este caso se hace de forma cualitativa, como se mencionó anteriormente, con la información que proporciona el espacio fase, ya que estas integrales pueden ser complicadas (funciones elípticas).[1] Ahora veamos cómo analizar estos puntos de equilibrio en el espacio fase. De acuerdo a la segunda ley de Newton se sabe que,
\[ \ddot{x}= \frac{F(x)}{m} = f(x) \] Es decir, se trata de una aceleración, la cual llamamos f(x). En lugar de trabajar solamente con la variable $x$, estamos interesados en ver el plano $x,\dot{x}$ por lo tanto se introduce la variable $y$
\[ \dot{x}=y \] \[ \dot{y}=f(x) \] Como se puede observar se ha pasado de una ecuación diferencial de segundo orden a un sistema de dos ecuaciones diferenciales de primer orden. Ahora tenemos un vector en el espacio fase \[ \vec{X}= (x,y) \] Observar que las ED las podemos escribir de la siguiente forma derivando a $\vec{X}$ \[ \vec{\dot{X}}= (y, f(x)) =\vec{V}(x,y) \] Es decir, en el lado derecho se tiene una función vectorial, o bien, el campo vectorial de la ecuación diferencial. Como se sabe la derivada del vector es la pendiente de la recta tangente de la trayectoria, que en este caso se encuentra en el espacio fase. Por lo tanto, la solución en el espacio fase va a ser tangente al campo vectorial.
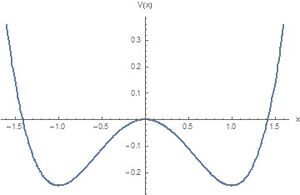
Por ejemplo, analicemos el potencial cuártico, el cual tiene dos puntos de equilibrio estable y uno inestable. El potencial esta dado por \[ V(x)= -\frac{1}{4}x^2 (2-x^2)= -\frac{x^2}{2}+ \frac{x^4}{4} \] Si graficamos este potencial nos da la forma de una función cuártica. Es decir, que para $x \rightarrow \pm\infty$, $V(x)\rightarrow +\infty$. Y además, $V(x=0)=0$. Por lo tanto, la fuerza asociada a este potencial es \[ F(x)= -\frac{dV}{dx}=x-x^3 \] La fuerza se anula justamente en los extremos del potencial, es decir, en $x=0$ y $x= \pm 1$. Ahora se evalúan estos puntos en el potencial $V(x=\pm 1)=-\frac{1}{4}$.
Como se menciono anteriormente introducimos la variable $y=\dot{x}$ y su derivada nos queda \[ \dot{x}= y \] \[ \dot{y}= F= x-x^3 \] En este análisis cualitativo se ha ignorado la masa, dado que es un factor de escala. Es decir, al multiplicar por m, nuestra expresión puede aumentar o disminuir su escala de forma positiva siempre, sin embargo, no altera el análisis dinámico.
Ecuación de Duffing
Si la resistencia de la varilla al movimiento la modelamos mediante un termino proporcional a la velocidad $- \gamma \dot{x}$, y la fuerza externa es de la forma $f \cos (\omega t)$, el sistema dinámico que describe la evolución del sistema es la ecuación de Duffing. \[ \ddot{x}+ \gamma \dot{x}-x+x^3= f \cos (\omega t) \]
Estudiaremos primero el caso sin fricción ni forzamiento $\gamma = 0$, $f=0$ y observaremos la solución para este caso conservativo, que representa esencialmente la dinámica de un sistema Hamiltoniano conservativo de un grado de libertad.
En segundo lugar agregaremos fricción $\gamma \neq 0 $ y veremos que hay cambios cualitativos notorios, pero no hay caos.
Por ultimo consideraremos el forzamiento $f \neq 0$ escogiendo la unidad de tiempo t tal que $\omega =1$. En este caso hay caos, una fuerte dependencia en las condiciones iniciales por la ocurrencia de las intersecciones homoclinicas.
Fuerza conservativa
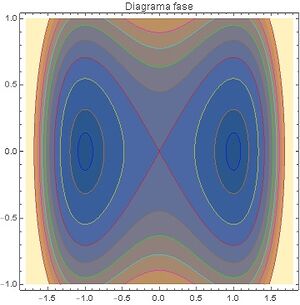
Para este primer supongamos que $\gamma=0$ y que $f=0$, por lo tanto la unica fuerza es la conservativa que depende de x. Dicho esto de la conservación de la energía tenemos \[ \frac{1}{2} \dot{x}^2 - \frac{1}{4}x^2 (2-x^2) \] Por lo tanto las curvas de energía son constantes, las cuales son las soluciones en el espacio fase con diferentes energías.
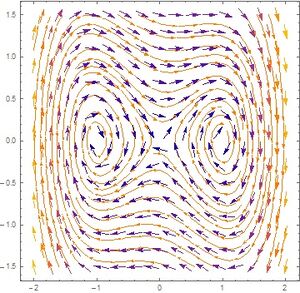
Para este caso doy valores iniciales distintos en los cuales pueda tener el cero y también el menor a $-\frac{1}{4}$ ya que lo mínimo que puede valor esta energía es $-\frac{1}{4}$ que es el valor para el cual nos encontramos en el fondo este potencial. En estas curvas de energía constante , el origen es un punto de equilibrio inestable de tipo silla es el que da lugar a la separatriz, con dos direcciones que entran llamadas variedades estables y dos que salen, llamadas variedades inestables.
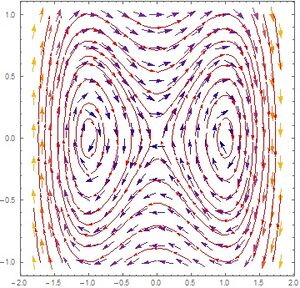
Podemos observar que el gráfico las flechas quedan tangentes al campo vectorial, observamos que hay 2 puntos de equilibrio, que son los centros de estas oscilaciones, a la izquierda y a la derecha del origen y el punto de equilibrio inestable que da lugar a una separatriz.
Lo que haremos primero es linealizar el campo vectorial cerca del equilibrio (0,0), queremos ver que pasa cerca de ese punto el cual es de tipo silla, para ello analizamos los puntos de equilibrio, esos son aquellos puntos donde el campo vectorial, el lado derecho de nuestras ED donde el campo vectorial se anula. Sabemos que nuestro campo vectorial es \[ \dot{x}=y \] \[ \dot{y}=F=x-x^3 \] Necesitamos que dicho campo sea igual a cero, entonces \[ \vec{\dot{X}}= \vec{V}(X) \] Vemos que si \[ \vec{V}(X_0)=0 \] Queremos desarrollar alrededor de $X_0$ entonces, en lugar de estudiar a cualquier x, quiero estudiar a $\vec{X}-\vec{X_0}$, entonces calculamos la derivada \[ \dot{(\vec{X}-\vec{X_0})} = \vec{V}(\vec{X_0})+ \frac{\partial \vec{V}}{\partial \vec{X}}(\vec{X}-\vec{X_0})+0 \] Notamos que $X_0$ es constante, haciendo un desarrollo de Taylor, para ordenes superiores no los tomo en cuenta.
Ahora como dijimos el campo vectorial se anulaba en $X_0$ el primer termino no da cero y escribimos explícitamente quienes son estas derivadas, lo cual es una matriz \[ \delta \vec{\dot{X}}= 0 + \begin{pmatrix} \frac{\partial V_1}{\partial x} & \frac{\partial V_1}{\partial y} \\ \frac{\partial V_2}{\partial x} & \frac{\partial V_2}{\partial y} \end{pmatrix}_{X_{0}} \delta \vec{X} \] Ahora si por notación a la matriz la llamamos L \[ \delta \vec{\dot{X}}= L_{X_0} \delta \vec{X} \] Esta ecuación me esta dando la dinámica cerca del equilibrio, como se mueven los puntos cercanos a $X_0$ y se mueven linealmente, como era de esperarse con la matriz L linealizada, al rededor del equilibrio y la dinámica es lineal por que nos detuvimos en primer orden.
Para calcular la separatriz, podemos encontrar las direcciones de las soluciones que llegan y salen localmente del punto de equilibrio inestable linealizando el campo vectorial cerca del origen \[ \begin{pmatrix} \delta \dot{x}\\ \delta \dot{y} \end{pmatrix}= \begin{pmatrix} \frac{\partial V_1}{\partial x} & \frac{\partial V_1}{\partial y} \\ \frac{\partial V_2}{\partial x} & \frac{\partial V_2}{\partial y} \end{pmatrix}_{(0,0)} \] La cual evaluada como lo muestra la ecuación en (0,0) no da como resultado \[ \begin{pmatrix} x\\ y \end{pmatrix}= \begin{pmatrix} 0&1\\ 1&0 \end{pmatrix}\begin{pmatrix} x\\ y \end{pmatrix} \] Una vez hecho esto obtenemos los valores y vectores propios de la matriz, los cuales están dados por $\lambda_1 =-1$ y $\lambda_2=1$ $\vec{u_1}= (-1,1)$ y $\vec{u_2}= (1,1)$.
El vector propio $\vec{u_1}$ indica la dirección estable, que tiende al origen cuando $t \rightarrow \infty$ pues decae exponencialmente a cero. El vector propio $\vec{u_2}$ es la dirección inestable que se aleja o sale del origen. En cuanto nos separamos de la vecindad donde es válida la aproximación lineal, deberemos considerar la solución no lineal completa, que en este caso tenemos explícitamente si utilizamos la ecuación de conservación de la energía. Nótese que las soluciones que salen del punto de equilibrio, denominadas las variedades inestables, coinciden en la parte no lineal con las que llegan al punto de equilibrio, denominadas las variedades estables. Este comportamiento de las separatrices es característico de los sistemas integrables.
Con fricción
Consideramos ahora una resistencia al movimiento proporcional a la velocidad $-\gamma x$. La energía deja de ser constante, el campo vectorial y el flujo fase se modifican por el término de fricción, como se muestra en la figura.
Por lo tanto consideramos ahora un efecto de fricción a nuestro potencial dado \[ \ddot{x} + \gamma \dot{x}-x +x^3=0 \]
Y nuestro campo vectorial quedaría de la siguiente forma \[ \dot{x}=y \] \[ \dot{y}=F=x-x^3- \gamma y \] Con esto suponemos un amortiguamiento proporcional a la velocidad, es decir lineal. Como se muestra en la imagen el diagrama fase ya no es simétrico va perdiendo energía hasta que entra a alguna de las cuencas de atracción (pozos de potencial) ya sea en el positivo o en el negativo $\pm1$ y al igual que el caso anterior el campo vectorial es tangente al flujo del espacio fase solución.
Ahora vamos a linealizar el campo vectorial cerca del origen
Siendo \[ V_1= y \] \[ V_2= F- \gamma y \] Por lo tanto para linealizar calculamos la matriz de derivadas parciales del campo vectorial, evaluado en el equilibrio (0,0) \[ L= \begin{pmatrix} \frac{\partial V_1}{\partial x} & \frac{\partial V_1}{\partial y} \\ \frac{\partial V_2}{\partial x} & \frac{\partial V_2}{\partial y} \end{pmatrix}_{(0,0)} \] Eso nos da como resultado la matriz linealizada \[ L= \begin{pmatrix} 0&1\\ 1& -\gamma \end{pmatrix} \] El punto de equilibrio continua siendo inestable de tipo silla. Y los valores propios de L son $\lambda_1= \frac{1}{2}(-\gamma-\sqrt{\gamma^2+4})$ y $\lambda_2= \frac{1}{2}(\sqrt{\gamma^2+4}-\gamma)$, con sus respectivos vectores propios $\vec{u_1}=(\frac{1}{2}(\gamma -\sqrt{\gamma^2 +4}),1) $ y $\vec{u_2}=(\frac{1}{2}(\gamma + \sqrt{\gamma^2+4}),1).$
Vemos que el primer valor propio es negativo y su correspondiente vector propio es la dirección de la variedad estable, mientras que el segundo es positivo y su correspondiente vector propio es la dirección de la variedad inestable. Si embargo, ahora las variedades estable e inestable del punto de equilibrio (0,0) no coinciden, como se ve en la figura. Una condición inicial arbitraria caerá eventualmente en alguno de los dos pozos del potencial, excepto aquellas con condiciones iniciales sobre la variedad estable, que tienden al punto de equilibrio inestable cuando $t \rightarrow \infty.$ La variedad estable divide el comportamiento cualitativo de las soluciones que caen atraídas por el punto de equilibrio estable izquierdo, de las que caen al punto de equilibrio estable derecho. Como puede verse no hay dependencia a las condiciones iniciales.
Con Forzamiento
Anteriormente estudiamos el caso del oscilador de Duffing amortiguado, con ecuación de movimiento \[ \ddot{x}+\gamma \dot{x}-x+x^3=0 \]
Este sistema no tiene una dependencia sensitiva a las condiciones iniciales. Si introducimos un forzamiento a esta ecuación de movimiento de la forma $f \cos (\omega t)$, donde $\omega$ es una frecuencia de forzamiento arbitraria, se tiene la ecuación de movimiento \[ \ddot{x}+\gamma \dot{x}-x+x^3= f \cos (\omega t) \] Ahora nuestro flujo fase tiene lugar en 3 dimensiones, por que debemos incluir el tiempo como una dimensión más.
Consideraremos que además de la fuerza no lineal dependiente de x, y de la fricción, se le aplica a una fuerza periódica dependiente de t, supondremos que la unidad de tiempo se elige tal que $\omega = 1$, por lo tanto tenemos \[ \ddot{x}+\gamma \dot{x}-x+x^3= f \cos (t) \]
Para este sistema no lineal y no autónomo es el oscilador de Duffing. En este caso se obtendrá la solución de forma numérica, con ayuda de Software, ya que no es posible obtener una solución analítica.
Los resultados numéricos obtenidos que son presentados a continuación, fueron realizados con los valores de $\gamma=0.2$ y $\omega=1$ y una amplitud de forzamiento $f=0.3$.
Ahora podemos observar que las trayectorias en el espacio fase se cruzan debido a que el sistema es no autónomo ya que dependen explícitamente de t. Para ver la solución única sin intersecciones, se debe extender el espacio fase e incluir a t como una coordenada.
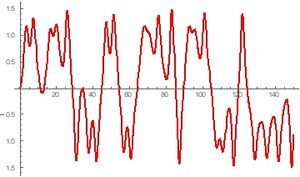
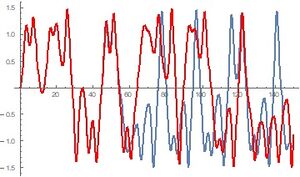
Esta dinámica revela un elemento al que no nos habíamos enfrentado anteriormente. El atractor no es una órbita periódica, sino una órbita de longitud infinita que se dobla y estira formando una estructura auto similar. Dos soluciones que inician cercanas evolucionan eventualmente en comportamientos muy diferentes, como se ve en la figura, debido a que el atractor extraño tiene una estructura fractal. A este comportamiento le llamamos el caos determinista, pues si bien el sistema está determinado por las ecuaciones diferenciales y condiciones iniciales de forma única, tiene una alta dependencia en las condiciones iniciales que hace que perdamos rápidamente capacidad de predicción.
¡Como podemos observar en las comparaciones de series de tiempo las soluciones dependen fuertemente de las condiciones iniciales!
Al movimiento que depende fuertemente de las condiciones iniciales se le llama movimiento caótico.[2]
Fernando M (discusión) 20:35 18 nov 2020 (CST)Mfgwi (discusión) 09:06 10 nov 2020 (CST)