Rejillas de difracción
Definición de difracción
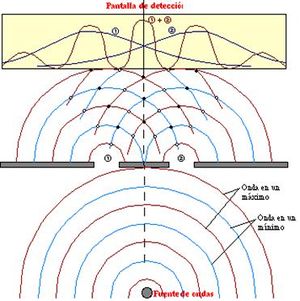
Es el fenómeno del movimiento ondulatorio en el que una onda de cualquier tipo se extiende después de pasar junto al borde de un objeto sólido o atravesar una rendija estrecha, en lugar de seguir avanzando en línea recta.
Principio de Huygens
La regla de Huygens dice: “cada punto de un frente de onda se considere como una nueva fuente de ondas esféricas”. Llamado principio de Huygens Cuando las ondas secundarias llegan a otro medio u objeto, cada punto del límite entre los medios se convierte en una fuente de dos conjuntos de ondas. El conjunto reflejado vuelve al primer medio, y el conjunto refractado entra en el segundo medio. Es más sencillo, y a veces suficiente, representar la propagación de la luz mediante rayos en vez de ondas. El rayo es la línea de avance, o dirección de propagación, de la energía radiante. En la óptica geométrica se prescinde de la teoría ondulatoria de la luz y se supone que la luz no se difracta. La trayectoria de los rayos a través de un sistema óptico se determina aplicando las leyes de reflexión y refracción.
Obstrucciones opacas
La difracción puede visualizarse como resultado de la interacción de ondas electromagnéticas con alguna clase de obstrucción física. Examinando la pantalla en una escala submicroscópica, imaginemos que debido al campo eléctrico de la radiación incidente la nube electrónica de cada átomo vibre. El modelo clásico, que habla de osciladores electrónicos que vibran y vuelven a emitir con la frecuencia de la fuente sirve muy bien, así que no necesitamos preocuparnos por la descripción cuántica.La amplitud y fase de un oscilador particular dentro de la pantalla están determinadas por el campo eléctrico local que las rodea, siendo éste una superposición del campo incidente y de los campos de todos los otros electrones vibrantes. Una pantalla grande opaca sin aberturas, hecha de papel negro o de hoja de aluminio, tiene un efecto obvio: no hay campo óptico en la región situada detrás de ella. Los electrones que se hallan cerca de la superficie iluminada se ponen a oscilar con la luz incidente, emitiendo energía radiante que es finalmente reflejada hacia atrás o absorbida por el material en forma de calor o ambas cosas.
Difracción de Fraunhofer y Fresnel
Imaginemos que tenemos una pantalla opaca,,que contiene una sola abertura pequeña iluminada por ondas planas de una fuente puntual,S, muy lejana. " En la imagen de Sucesión"
El plano de observaciones es una pantalla paralela y muy cercana a ,. Bajo estas condiciones, se prollecta sobre la pantalla una imagen de la abertura que es claramente reconocible a pesar de unas pequeñas franjas que se ven alrededor de su periferia "En la imagen de difracción a distancias".Según el plano de observación va alejándose de , la imagen de la abertura, si bien es aún fácilmente reconocible, va adquiriendo más estructura mientras que las franjas se vuelven más prominentes. Este fenómeno se denomina difracción de Fresnel o de campo cercano. Si se va alejando aún más el plano de observación, se producirá un cambio continuo en las franjas. A una gran distancia de la distribución proyectada se habrá extendido considerablemente, teniendo muy poco o nada de parecido con la abertura real. De ahí en adelante, el movimiento de cambia esencialmente sólo el tamaño de la distribución y no su forma. Esta es la difracción de Fraunhofer o de campo lejano.
Este fenómeno se denomina difracción de Fresnel o de campo cercano. Si se va alejando aún más el plano de observación, se producirá un cambio continuo en las franjas. A una gran distancia de , la distribución proyectada se habrá extendido considerablemente, teniendo muy poco o nada de parecido con la abertura real. De ahí en adelante, el movimiento de , cambia esencialmente sólo el tamaño de la distribución y no su forma. Consideremos una fuente puntual S y un punto de observación P, donde ambos estén muy lejos de , y donde no haya lentes."En la imagen de sombra".
Figura 3.
(a) la sombra de la mano de María sujetando una moneda, proyectada directamente en una película. (b) difracción de Fresnel de electrones producida por cristales de óxido de cinc. Siempre que la onda incidente y la emitida sean planas (difiriendo de ello en una pequeña fracción de la longitud de onda) en la extensión de las aberturas difractoras (u obstáculos), se obtiene la difracción de Fraunhofer. [1].
Varios osciladores coherentes
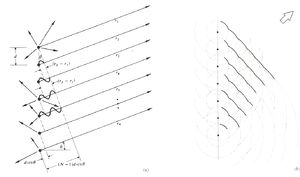
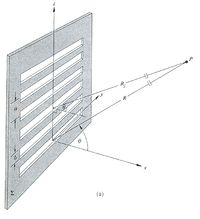
La ilustración "De osciladores" muestra un conjunto lineal de N osciladores puntuales coherentes (o antenas emisoras), todos ellos idénticos incluso en su polarización. Todos los rayos que se muestran son casi paralelos, encontrándose en un punto P muy distante. Si la extensión espacial del conjunto es comparativamente pequeña, las amplitudes de onda individuales que lleguen a P serán esencialmente iguales, habiendo recorrido casi las mismas distancias, esto es.
(Disposición lineal de osciladores coherentes en fase:
(a)Obsérvese que en el ángulo mostrado mientras que en , sería cero.
(b) Una de las muchas series de frentes de onda emitidos por una línea de fuentes coherentes.)
La suma de los trenes de onda esféricos interferentes produce un campo eléctrico en P proporcionado por la parte real de
La diferencia de fase entre fuentes adyacentes se obtiene de la expresión , y puesto que
, en un medio con índice . Utilizando "La imagen de osciladores",se deduce que
, ,etc.
Entonces, el campo en P puede escribirse como
X
La serie geométrica entre paréntesis tiene el valor
que puede ordenarse así:
o de manera equivalente
Entonces el campo se transforma en
Obsérvese que si definimos R como la distancia desde el centro de la línea de los osciladores hasta el punto P, es decir
entonces la ecuación (10.3) se convierte en
Finalmente, la distribución de densidad de flujo dentro de la distribución de difracción debida a N fuentes puntuales distantes, idénticas y coherentes en una disposición lineal, es proporcional a EE*/2 para E compleja o
donde es la densidad de flujo que saliendo desde cualquier fuente puntual llegue a P . La dependencia funcional de I con queda más clara en la forma
El término se somete a unas fluctuaciones rápidas, mientras que la función que la modula , varia de manera relativamente lenta. La expresión combinada da lugar a una serie de picos principales agudos separados por picos pequeños complementarios. Los máximos principales se dan en dirección , tales que , donde . Dado que
Sólo exite m=0 o máximo principal de orden cero. Si estuviéramos mirando una fuente lineal idealizada de osciladores electrónicos separados por distancias atómicas, podríamos esperar sólo ese máximo principal en el campo luminoso. El conjunto de antenas "En la imagen de radiotelescopio" puede transmitir radiación en el haz estrecho o lóbulo que corresponde a un máximo principal.
Supongamos que tenemos un sistema en el que podemos introducir un desplazamiento intrínseco de fase entre osciladores adyacentes.
En ese caso
Los varios máximos principales se darán en nuevos ángulos
Centrándose en el máximo central m=0, puede variarse su orientación a voluntad ajustando simplemente el valor de
Cada punto emite una ondita esférica que escribimos como
indicando explícitamente la dependencia de la amplitud con el inverso de r.La cantidad se denomina eficacia de la fuente. La contribución del segmento i a la intensidad del campo eléctrico en P es, por consiguiente,
siempre que sea tan pequeña que la diferencia relativa de fase de los osciladores en su interior sea despreciable y sus campos se sumen constructivamente. Al mismo tiempo que N tiende a infinito, las eficacias de fuente de los osciladores individuales tienen que disminuir hasta casi cero si la salida total debe conservarse finita. Definir una constante como la eficacia de fuente por unidad de longitud de la composición, es decir,
El campo neto en P de todos los segmentos M es
La suma se transforma entonces en una integral definida
Difracción de Fraunhofer
La rendija única
Bajo estas circunstancias r(y) nunca se desvía sensiblemente de su valor medio R, de tal manera que la cantidad en P es esencialmente constante para todos los elementos dy.
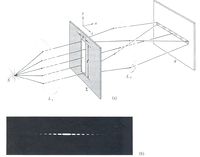
donde dy es la amplitud de la onda. En la "Imagen de fraunhofer";el ancho de una abertura de este tipo puede ser de varios cientos y su longitud medir unos pocos centímetros.
(a)difracción de Fraunhofer producida por una sola rendija. (b)distribución de difracción de una sola rendija vertical en iluminación con fuente puntual.
El procedimiento usual a seguir en el análisis es dividir la rendija en una serie de tiras diferenciales largas (dz por l), paralelas al eje y, como se muestra "En la imagen de DIFRACCIÓN".
Difracción
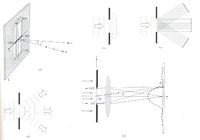
(a) El punto P en se halla a una distancia infinita de . (b) Trenes de onda de Huygens emitidos en la apertura. (c) Representación equivalente en términos de rayos. Cada punto emite rayos en todas las direcciones. Los rayos paralelos en distintas direcciones son visibles. (d) Estos haces de rayos corresponden a ondas planas que pueden considerarse como componentes de Fourier tridimensionales. (e) Una rendija única iluminada por ondas planas monocromáticas.
Véase también
La doble rendija
Al principio podría parecer "En la imagen de distancia infinita" que la ubicación del máximo principal está siempre en línea con el centro de la abertura difractora; esto,sin embargo, por lo general no es cierto.
(a)El punto P se halla a una distancia infinita de .
La figura de difracción está en realidad centrada alrededor del eje de la lente y tiene exactamente la misma forma y ubicación, independientemente de la posición de la rendija,siempre que no se cambie su orientación y las aproximaciones sean válidas . Supongamos ahora que tenemos dos rendijas largas de ancho b y una separación a de centro a centro "En la imagen de doble rendija".
Cada abertura, por sí misma, generaría la misma figura de difracción de rendija única en la pantalla de visualización .
En cualquier punto en , las contribuciones de las dos rendijas se superponen y, si bien la amplitud de cada cual tiene que ser esencialmente igual, sus fases pueden diferir significativamente.
La contribución total al campo eléctrico, en la aproximación de Fraunhofer
La integración de la ecuación (10.22) proporciona
Difracción por muchas rendijas
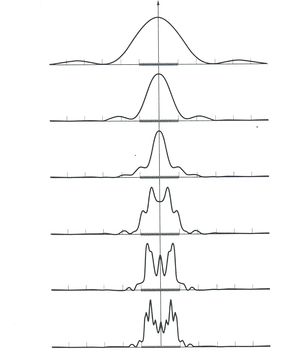
El procedimiento para obtener la función de irradiancia para una onda monocromática difractada por muchas rendijas es esencialmente el mismo que se utilizó al analizar dos rendijas. Consideremos el caso de N rendijas estrechas, largas y paralelas, cada una de ancho b y una separación a de centro a centro, como "En la imagen de rendijas múltiples".
(El punto P en se halla nuevamente a una distancia infinita de ).
Con el origen del sistema coordenado una vez más en el centro de la primera rendija, la perturbación óptica total en un punto en la pantalla está proporcionada por
donde,como antes, . Esto se aplica a la condición de Fraunhofer, de tal manera que la configuración de la abertura debe ser tal que todas las rendijas estén cerca del origen mientras que la aproximación.
La elección de una rejilla
La selección de un estándar de rejilla de Optometría Requiere la consideración de un numero de variables relacionadas con el uso previsto de la reja es. Estos son los siguientes:
Eficiencia: En general, gobernó rejillas tienen una mayor eficiencia que las rejillas holográficas. Aplicaciones como la excitación de fluorescencia y otras rejilla (ver las curvas de eficiencia para la comparación). Como regla general, la eficiencia de primer orden de una rejilla gobernó disminuye en un 50% a los dos tercios y tres partes de la longitud de onda incendio.
Longitud de onda Blaze: rejillas gobernados, debido a su "diente de sierra" perfil de la ranura, tienen un pico relativamente fuerte en torno a su longitud de onda incendio, mientras que algunas rejillas holográficas tienen una respuesta más plano espectral. Aplicaciones en torno a un rango de longitud de onda estrecho podrían beneficiarse de una rejilla gobernó ardió en esa longitud de onda.
Rango de longitud de onda: El rango espectral cubierto por una rejilla de separación depende de la ranura y es el mismo de las rejillas para descartar y holográfico con la rejilla misma constante.
La luz difusa: Para aplicaciones tales como la espectroscopia Raman, donde la señal-ruido es fundamental, inherente a la poca luz de dispersión de una red de difracción holográfica es una ventaja.
Poder de resolución: No hay diferencia en la potencia de resolución de holográfica y gobernó con rejillas de separación ranura idénticos rejillas de manejo La superficie de las rejillas estándar están recubiertos con aluminio u oro y requieren un cuidado extremo al manejar. El manejo debe ser realizado por los bordes. Estos recubrimientos relativamente suaves son vulnerables a las huellas dactilares y numerosos aerosoles.
Polarización
Curvas típicas de eficiencia muestran que, en todos los casos, la orientación de la polarización del vector E ti (P-Plane) perpendicular de las ranuras (E) aumenta la eficiencia en una región de longitud de onda específica. Esto debe ser considerado cuando la optimización de la figura de mérito (Q) de una cavidad, en particular cuando se polariza de componentes auxiliares, tales como ángulo de Brewster ventanas















![[1+(e^{i\delta})+(e^{i\delta})^2+(e^{i\delta})^3+{...}+(e^{i\delta})^{N-1}]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/21d8ab8652e748321b9b2b783056c11560630bc5)

![\frac{{e^{iN\delta/2}[e^{iN\delta/2}-e^{iN\delta/2}]}}{e^{i\delta/2}[e^{i\delta/2}-e^{i\delta/2}]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/d724f655e5c3d46dabbad9cc8e2ded7a32c2cd8e)

![E ={E_o(r)e^{-i\omega*t}e^{i[kr_1+(N-1)\delta/2]}}\frac{{senN\delta/2}}{sen\delta/2}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/b10b6bb2027e63c3962f4aeb506a424dffcb5a9f)





![I={I_o}\frac{{sen^2[N(kd/2)sen\theta]}}{sen^2[(kd/2)sen\theta]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/efb7f57331132788523b6018f98d1f3409eccf4c)
![{sen^2[N(kd/2)sen\theta]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/39ce26b75e78743262069acb5ea797f3e0547ba6)
![{{sen[kd/2)sen\theta]}^{-2}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/249c9cb842e76a9c887a933b3a4af915bbbc6a41)
























![E=bc(\frac{sen\beta}{\beta})[sen(\omega*t-kR)+sen(\omega*t-kR+2\alpha)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/09d773d7215387746f6394eeed9522312b51d5c4)
![F(z)={sen[\omega*t-k(R-zsen\theta)]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/8897841797b7c840d17530729d09ab9326b1d5fa)

