Radiacion: Reflexion en metales

Reflexión en metales

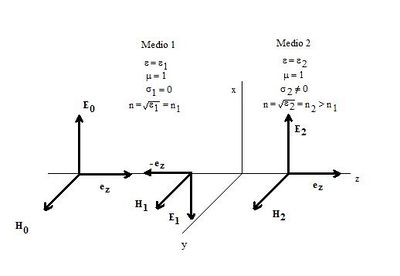
Dibujo de una onda incidente $\mathbf {E_{0}}$, reflejada $\mathbf {E_{1}}$ y transmitida $\mathbf {E_{2}}$ para la frontera entre un dieléctrico y un conductor

En este tema veremos la reflexión de una onda electromagnética cuando la frontera está limitada por un dieléctrico y un conductor. Tomaremos una onda electromagnética plana que incide sobre la frontera (que es una superficie plana). Veremos el caso de incidencia normal.

En nuestro caso, siguiendo el dibujo, el eje en el cual se mueven nuestras ondas es el Z. Veamos la onda incidente, la reflejada y transmitida.

Onda incidente:

$\mathbf {E_{0}} =\mathbf {e_{x}} E_{0}^{0}e^{i(k_{1}Z-\omega t)}$

$\mathbf {H_{0}} =\mathbf {e_{y}} {\frac {c}{\omega }}k_{1}E_{0}^{0}e^{i(k_{1}Z-\omega t)}$

Onda reflejada:

$\mathbf {E_{1}} =-\mathbf {e_{x}} E_{1}^{0}e^{i(-k_{1}Z-\omega t)}$

$\mathbf {H_{1}} =\mathbf {e_{y}} {\frac {c}{\omega }}k_{1}E_{1}^{0}e^{i(k_{1}Z-\omega t)}$

Onda transmitida:

$\mathbf {E_{2}} =\mathbf {e_{x}} E_{2}^{0}e^{i({\tilde {k_{2}}}Z-\omega t)}$

$\mathbf {H_{2}} =\mathbf {e_{y}} {\frac {c}{\omega }}{\tilde {k_{2}}}E_{2}^{0}e^{i({\tilde {k_{2}}}Z-\omega t)}$

En la onda reflejada, notamos que el vector $\mathbf {E_{1}}$ tiene la $\mathbf {e_{x}}$ negativa. Esto sucede porque hay un cambio de fase en la onda reflejada de $\pi$.

La constante de propagación ${\tilde {k_{2}}}$ del conductor es:

${\tilde {k_{2}}}^{2}={\frac {\omega ^{2}\epsilon _{2}}{c^{2}}}(1+i{\frac {4\pi \sigma _{2}}{\omega \epsilon _{2}}})$ ... (*)

Esto es porque, tomando la ecuación para una onda propagándose en un medio conductor:

${\frac {\partial ^{2}\mathbf {E} }{\partial Z^{2}}}-{\frac {\epsilon \mu }{c^{2}}}{\frac {\partial ^{2}\mathbf {E} }{\partial t^{2}}}-{\frac {4\pi \sigma \mu }{c^{2}}}{\frac {\partial \mathbf {E} }{\partial t}}=0$ ... (2*)

Y además tomando las soluciones de onda plana para la ecuación de Maxwell:

$\mathbf {E} =\mathbf {E_{0}} e^{i(kZ-\omega t)}$

Veamos las derivadas de ésta ecuación:

${\frac {\partial ^{2}\mathbf {E} }{\partial Z^{2}}}=\mathbf {E_{0}} k^{2}e^{i(kZ-\omega t)}$

${\frac {\partial \mathbf {E} }{\partial t}}=\mathbf {E_{0}} (-\omega )e^{i(kZ-\omega t)}$

${\frac {\partial ^{2}\mathbf {E} }{\partial t^{2}}}=\mathbf {E_{0}} \omega ^{2}e^{i(kZ-\omega t)}$

Estas ecuaciones las sustituimos en la ecuación (2*) y nos resulta lo siguiente:

$[k^{2}-i{\frac {4\pi \omega \sigma \mu }{c^{2}}}-{\frac {\epsilon \mu \omega ^{2}}{c^{2}}}]\mathbf {E_{0}} e^{i(kZ-\omega t)}=0$

Podemos decir que:

$[k^{2}-i{\frac {4\pi \omega \sigma \mu }{c^{2}}}-{\frac {\epsilon \mu \omega ^{2}}{c^{2}}}]=0$

En ese sentido podemos despejar $k^{2}$ y llegamos a:

${\tilde {k_{2}}}^{2}={\frac {\mu \omega ^{2}\epsilon }{c^{2}}}(1+i{\frac {4\pi \sigma }{\omega \epsilon }})$

Que es la constante de propagación para conductores, que como vemos es compleja (Por eso le ponemos la tilde). Para nuestro caso $\mu =1$.

La constante de propagación $k_{1}$ para el dieléctrico es:

${\frac {c}{\omega }}k_{1}=n_{1}$

Sabemos que los campos vectoriales satisfacen las siguientes condiciones en la frontera entre dos medios:

$\mathbf {E} :$ Componente tangencial continuo

$\mathbf {H} :$ Componente tangencial continuo (para el caso de superficies sin corriente)

Por otro lado, viendo las ondas, tenemos que del lado izquierdo de la frontera tenemos la onda incidente y reflejada y del lado derecho tenemos la transmitida; y además que la cantidad de energía total se conserva nos daría en lenguaje matemático lo siguiente:

Del lado izquierdo:

$\mathbf {E} (Z,t)=\mathbf {e_{x}} E_{0}^{0}e^{i(k_{1}Z-\omega t)}-\mathbf {e_{x}} E_{1}^{0}e^{i(-k_{1}Z-\omega t)}$

$\mathbf {H} (Z,t)=\mathbf {e_{y}} {\frac {c}{\omega }}k_{1}E_{0}^{0}e^{i(k_{1}Z-\omega t)}+\mathbf {e_{y}} {\frac {c}{\omega }}k_{1}E_{1}^{0}e^{i(k_{1}Z-\omega t)}$

Del lado derecho:

$\mathbf {E} (Z,t)=\mathbf {e_{x}} E_{2}^{0}e^{i({\tilde {k_{2}}}Z-\omega t)}$

$\mathbf {H} (Z,t)=\mathbf {e_{y}} {\frac {c}{\omega }}{\tilde {k_{2}}}E_{2}^{0}e^{i({\tilde {k_{2}}}Z-\omega t)}$

Usando las ecuaciones para $\mathbf {E}$ y $\mathbf {H}$ y usando que en la frontera sus componentes tangenciales son continuas, dicho de otra manera: el lado izquierdo es igual al lado derecho en la frontera ($Z=0$) tenemos lo siguiente:

$\mathbf {E} :\mathbf {e_{x}} E_{0}^{0}e^{i(k_{1}0-\omega t)}-\mathbf {e_{x}} E_{1}^{0}e^{i(-k_{1}0-\omega t)}=\mathbf {e_{x}} E_{2}^{0}e^{i({\tilde {k_{2}}}0-\omega t)}$

$\mathbf {H} :\mathbf {e_{y}} {\frac {c}{\omega }}k_{1}E_{0}^{0}e^{i(k_{1}0-\omega t)}+\mathbf {e_{y}} {\frac {c}{\omega }}k_{1}E_{1}^{0}e^{i(k_{1}0-\omega t)}=\mathbf {e_{y}} {\frac {c}{\omega }}{\tilde {k_{2}}}E_{2}^{0}e^{i({\tilde {k_{2}}}0-\omega t)}$

Esto nos da:

$E_{0}^{0}-E_{1}^{0}=E_{2}^{0}$

$k_{1}(E_{0}^{0}+E_{1}^{0})={\tilde {k_{2}}}E_{2}^{0}$

Resolviendo las ecuaciones para escribir la magnitud de la onda reflejada y transmitida en términos de la incidente, quedaría de la siguiente manera:

$E_{1}^{0}={\frac {{\tilde {k}}_{2}-k_{1}}{{\tilde {k}}_{2}+k_{1}}}E_{0}^{0}$ ... (1)

$E_{2}^{0}={\frac {2k_{1}}{{\tilde {k}}_{2}+k_{1}}}E_{0}^{0}$

Aquí podemos notar que éstas ecuaciones son generales en el sentido de que sí ${\tilde {k_{2}}}$ fuera real, es decir $k_{2}={\frac {\omega }{c}}n_{2}$ tendríamos la descripción para el caso de un dieléctrico:

$E_{1}^{0}={\frac {n_{2}-n_{1}}{n_{2}+n_{1}}}E_{0}^{0}$

$E_{2}^{0}={\frac {2n_{1}}{n_{2}+n_{1}}}E_{0}^{0}$

Por otro lado, si sustitumos el valor de $k_{1}={\frac {\omega }{c}}{\sqrt {\epsilon _{1}}}$ y el de ${\tilde {k}}_{2}$ en las ecuaciones anteriores, tendríamos lo siguiente:

$E_{1}^{0}={\frac {{\sqrt {{\frac {\epsilon _{2}}{\epsilon _{1}}}(1+i{\frac {4\pi \sigma _{2}}{\epsilon _{2}\omega }})}}-1}{{\sqrt {{\frac {\epsilon _{2}}{\epsilon _{1}}}(1+i{\frac {4\pi \sigma _{2}}{\epsilon _{2}\omega }})}}+1}}E_{0}^{0}$

$E_{2}^{0}={\frac {2}{{\sqrt {{\frac {\epsilon _{2}}{\epsilon _{1}}}(1+i{\frac {4\pi \sigma _{2}}{\epsilon _{2}\omega }})}}+1}}E_{0}^{0}$

Estas ecuaciones siguen siendo generales y a partir de ellas podemos ver los casos particulares que se generan bajo ciertas condiciones, veamos:

1. Si el medio 2 es un conductor perfecto, es decir cuando $\sigma _{2}$ tiende a infinito, tendríamos lo siguiente:

$E_{1}^{0}=E_{0}^{0}$

$E_{2}^{0}=0$

Estas dos ecuaciones nos dicen lo mismo pero de manera diferente. La primera dice que la amplitud de la onda reflejada es igual a la incidente (y nada más), es decir, no hay transmisión. La segunda nos dice que la amplitud de la onda transmitida es cero, es decir, no hay transmisión, por lo tanto la amplitud incidente es igual a la reflejada.

2. Si el medio es un dieléctrico, es decir $\sigma =0$, tendríamos las ecuaciones para dieléctricos.

Conductor no perfecto

Sabemos la constante de propagación para un conductor es compleja, es decir, podemos escribirla de la siguiente manera:

${\tilde {k_{2}}}=\alpha +i\beta$

Elevandola al cuadrado para después compararla con la original (Ecuación *), tenemos:

${\tilde {k_{2}}}^{2}=(\alpha ^{2}-\beta ^{2})+2i\alpha \beta$

Tomamos esta ecuación y comparamos su parte real e imaginaria con la Ecuación (*) y tendríamos:

$\alpha ={\frac {\omega }{c}}{\sqrt {\frac {\epsilon _{2}}{2}}}[{\sqrt {1+({\frac {4\pi \sigma _{2}}{\omega \epsilon _{2}}})^{2}}}+1]^{1/2}$

$\beta ={\frac {\omega }{c}}{\sqrt {\frac {\epsilon _{2}}{2}}}[{\sqrt {1+({\frac {4\pi \sigma _{2}}{\omega \epsilon _{2}}})^{2}}}-1]^{1/2}$

Ahora, si hacemos una aproximación de que el medio 2 es buen conductor pero no es perfecto, es decir, ${\frac {4\pi \sigma _{2}}{\epsilon _{2}\omega }}>>1$ podemos desarrollar lo siguiente:

$\alpha \cong {\frac {\omega }{c}}{\sqrt {\frac {\epsilon _{2}}{2}}}[{\sqrt {({\frac {4\pi \sigma _{2}}{\omega \epsilon _{2}}})^{2}}}]^{1/2}$

Obtenemos este resultado ya que como ${\frac {4\pi \sigma _{2}}{\epsilon _{2}\omega }}$ es grande, se pueden despreciar el $1$ que se suma tanto fuera como dentro de la raíz cuadrada. Lo mismo hacemos para $\beta$ y llegamos al siguiente resultado:

$\alpha \cong \beta \cong {\frac {1}{c}}{\sqrt {2\pi \omega \sigma _{2}}}$

Y entonces ${\tilde {k_{2}}}$ podemos expresarlo de la siguiente manera:

${\tilde {k_{2}}}=\alpha +i\beta \cong (1+i){\frac {\sqrt {2\pi \omega \sigma _{2}}}{c}}$

Donde ${\frac {\sqrt {2\pi \omega \sigma _{2}}}{c}}\equiv \delta$ es la definición de Skin Depth o Efecto Pelicular.

Entonces la constante de propagación se puede escribir de la siguiente manera:

${\tilde {k_{2}}}\cong {\frac {1+i}{\delta }}$

Además, la longitud de onda de la radiación indicente con frecuencia $\omega$ es $\lambda ={\frac {c}{\omega }}$. Aplicando esta ecuación en la anterior:

${\frac {c}{\omega }}{\tilde {k_{2}}}=(1+i){\frac {\lambda }{\delta }}$

Por otro lado, sabemos que:

${\frac {c}{\omega }}k_{1}=n_{1}$

Sustituyendo los valores de ${\tilde {k_{2}}}$ y $k_{1}$ en la ecuación (1):

$E_{1}^{0}={\frac {(1+i)({\frac {\lambda }{\delta }})-n_{1}}{(1+i)({\frac {\lambda }{\delta }})+n_{1}}}E_{0}^{0}$

El coeficiente de reflexión R, está dado de la siguiente manera:

$R={\frac {|E_{1}^{0}|^{2}}{|E_{0}^{0}|^{2}}}={\frac {[1-({\frac {\delta }{\lambda }})n_{1}]^{2}+1}{[1+({\frac {\delta }{\lambda }})n_{1}]^{2}+1}}$

Para frecuencias ópticas ${\frac {\delta }{\lambda }}$ es pequeño comparado con la unidad. Por tanto, podemos tener la aproximación $({\frac {\delta }{\lambda }})n_{1}<<1$ que nos daría, expandiendo la ecuación anterior:

$R\cong 1-2{\frac {\delta }{\lambda }}n_{1}$

o lo mismo:

$R\cong 1-2n{\sqrt {\frac {v}{\sigma _{2}}}}$

Aquí podemos ver que esta ecuación es una generalización. Veamos los casos:

1. Si $\sigma _{2}$ tiende a infinito, nos daría:

$R\cong 1$

Esto quiere decir que la reflexión es cercana a ser total, es decir, casi no hay transmisión (se puede despreciar).

2. Si $\sigma _{2}$ se va acercando a cero, R disminuye. Esto quiere decir que empieza a disminuir la reflexión porque ya hay transmisión.

Referencia

Jerry B. Marion, Mark A. Heal. Classical Electromagnetic Radiaton. Second Edition

http://maxwell.ugr.es/innov/visua0506/librorgomez/librorgomez.htm

Vínculos

Aquí hay una aplicación de Java muy buena:

http://www.sociedadelainformacion.com/departfqtobarra/ondas/refraccion/refraccion.html

---

Aportación por usuario: Salvador Toledo Nuñez

---