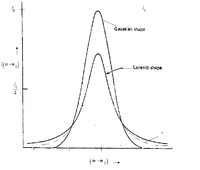
Perfil De Línea Y Ensanchamiento

Ensanchamiento de líneas espectrales

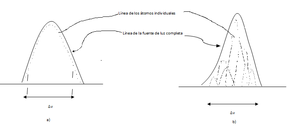
Nunca es perfectamente monocromática, sino que tiene un ancho infinito, bien sea en escala de frecuencia o longitudes de onda. Es importante mencionar que al medir esta anchura la medición no se hace para un solo átomo, sino para todo el conglomerado de átomos que forman la fuente luminosa. El ensanchamiento se dice que es homogéneo si el ancho de la línea para el conjunto de átomos es igual al ancho de la línea de cada átomo individual, como se muestra en la figura 1(a).El ensanchamiento se dice que es inhomogéneo si el ancho de la línea para el conjunto de átomos no es el producido por cada átomo de manera individual, sino el debido a una distribución estadística en sus longitudes de onda y sus irradiancia relativas, como se ve en la figura 1(b)

Figura 1. Tipos ensanchamiento de líneas espectrales: a)ensanchamiento homogéneo. y b) ensanchamiento inhomogéneo

El ensanchamiento homogéneo puede deberse a una o más de las siguientes causas:

a) Ensanchamiento natural

b) Colisiones entre átomos, que también se conoce como ensanchamiento de presión

El ensanchamiento inhomogéneo puede deberse a las siguientes causas

a) Ensanchamiento de Doppler.

b) Variaciones estadisticas en las posiciones de los niveles de energia.

Una explicación clásica del ensanchamiento natural es que el tren de ondas no es infinitamente largo, sino corto, debido a que el oscilador sólo está emitiendo la onda durante un cierto tiempo igual a la vida media del estado. Desde un punto de vista cuántico podemos pensar que ay una incertidumbre en la determinación del instante en el que fue emitido el fotón no está perfectamente definida debido al principio de incertidumbre de Heisenberg. De la figura 1) podemos ver que el ancho Δν está dado de manera aproximada por $\Delta {\nu }={\frac {c}{L}}$

Donde L es la longitud del tren de ondas, o de forma equivalente, de la ecuación $L=c{\tau }$ y si sustituimos en la ecuación anterior L obtenemos que $\Delta {\nu }={\frac {1}{\tau }}$

$\Delta {\nu }={\frac {c}{2\pi L}}={\frac {c}{2\pi \tau }}$

Debido a las colisiones de la línea se puede ensanchar aún más. La interpretación clásica es que el tren de ondas se hace todavía más corto, debido a que el átomo colisiona con otro, interrumpiendo así su emisión. Entonces, parte de la energía es emitida antes de la colisión como luz y parte se transfiere al otro átomo durante ella. En una fuente de luz gaseosa, al aumentar la presión del gas el número de colisiones aumenta y el camino medio libre entre colisiones disminuye. El camino medio libre determina la longitud del tren de ondas. Este tipo de colisión se conoce como colisión inelástica.

PERFIL DE LÍNEA: Es una curva que indica la variación interna de la intensidad de una línea espectral de un cuerpo.

La mecánica cuántica establece que cada átomo cuenta con un conjunto de niveles de energía bien definido. El espectro de energía es discreto y las transiciones entre niveles deben seguir ciertas reglas, dependiendo del tipo de interacción que produce la excitación.

En muestras atómicas a baja presión las transiciones entre niveles de energía ocurren principalmente por absorción y emisión de radiación electromagnética. El conjunto de frecuencias de la radiación involucrada en las transiciones forma el espectro de absorción o emisión del elemento en cuestión.

Cuando un átomo interactúa con radiación, existen tres procesos por los que puede cambiar de estado energético: absorción, emisión espontánea y emisión estimulada. Los cambios en energía están estrechamente relacionados con cambios en las poblaciones de los niveles atómicos.

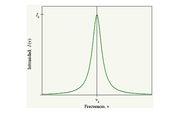
Al estudiar más detalladamente una transición entre los niveles inferior y superior con energías $E_{1}$ y $E_{2}$ respectivamente, se encuentra que alrededor de la frecuencia central de la transición $\ (\omega =(E_{2}-E_{1})/h)$ existe una distribución espectral I(ω). Donde h es La constante de Planck, se simbolizada con la letra h (o bien ħ=h/2π), En la vecindad de $\omega _{0}$ la función I (ω) es conocida como el perfil de línea. En la vecindad de $\omega _{0}$ la función I(ω) es conocida como el perfil de línea. El intervalo de frecuencias $\gamma =|\omega _{2}-\omega _{1}|$ entre las frecuencias $\omega _{1}$ y $\omega _{2}$ tales que $I(\omega _{1})=(\omega _{2})$ es llamado ancho completo en la mitad del máximo o simplemente el ancho de banda de la línea espectral. El significado físico del ancho de banda es la incertidumbre con que puede ser medida la frecuencia de la transición entre los niveles (1) y (2).

En el caso del espectro de absorción se tiene una diferencia significativa en el comportamiento de los átomos. Cuando todos los átomos de una muestra que se encuentran en el nivel inferior $E_{1}$ tienen la misma probabilidad $P_{1}2(\omega )$ de absorber una onda electromagnética de frecuencia ω, se dice que el ensanchamiento de la línea espectral es homogéneo, en otro caso se habla de un ensanchamiento inhomogéneo.

Ancho equivalente de una línea

El ancho equivalente $(w\lambda$ de una línea, se define como el ancho medido en ángstrongs de una caja rectangular que contiene una área igual a la contenida por la línea espectral, ó , el área medida entre el nivel del continuo, normalizado ala unidad y con referencia cero.

$(w\lambda =\int {\frac {f_{o}(\lambda )-f_{c}(\lambda )}{f_{c}(\lambda )}}d\lambda =\int R_{\lambda }d\lambda$

Donde:

$(f_{o}(\lambda )$ Es la densida de flujo observado

$(f_{c}(\lambda )$ Es nivel de conjunto por debajo de la línea

La anchura y la forma del espectro de líneas importancia:

a) Pueden proporcionar información a una temperatura, la densidad y la composición actual de la fuente

b) El cálculo detallado de la interacción de los átomos de ancho radiación requieren un conocimiento exacto del perfil de la línea

c) El perfil de la línea es importante para determinar muchas de las características de los láseres de gas.

Ancho de banda natural

Todos los espectros atómicos presentan un ensanchamiento "natural", llamado de esta manera porque su origen está intrínsecamente relacionado a las transiciones atómicas. El perfil de línea asociado a este ensanchamiento tiene como característica ser Lorentziano.

Para mostrar de manera clara el origen del ensanchamiento y el carácter Lorentziano del perfil de línea se utilizará el hecho de que la emisión y la absorción pueden ser entendidos como procesos inversos. Primero se muestra que efectivamente el perfil de línea de las líneas de emisión es Lorentziano para posteriormente describir el ensanchamiento de los espectros de absorción.

El principio de incertidumbre de Heinsemberg para la energía. El tiempo exacto durante el cual permanece en ese estado no es el mismo en cada decaimiento; es aleatorio, por lo que no se puede calcular analíticamente. Después de otro tiempo τ, de los electrones que quedaban en estado excitado, una fracción similar decaerá. Es decir, población de electrones en estado excitado disminuirá de forma exponencial. Expresado en forma de ecuación, el número de electrones en el estado excitado a un tiempo t será:

$n(t)=n(0)e^{-{\frac {(t)}{(\tau )}}}$

Donde n(t) número de electrones en estado excitado en un tiempo t y n(0) número de electrones en estado excitado que había en un principio. El flujo de radiación emitido por estos electrones también será una función exponencial decreciente:

$L(t)=n(0)e^{-\delta t}$ como se ve en la Figura (1)

Con $\delta$, una constante que nos indica la tasa de decaimiento del Ensanchamiento natural de una línea de emisión.

Ensanchamiento natural de una línea de emisión. La línea adquiere un perfil Lorentziano.

Típicamente, una línea espectral ensanchada de forma natural tiene un ancho a media altura en un rango entre 0.1 a 100 MHz o, en términos de longitud de onda, entre 10 − 4 y 10 − 7 nm. En su forma más sencilla, el ancho a media altura para el ensanchamiento natural se puede calcular a través de la siguiente expresión:

$\delta \nu _{L}={\frac {e^{2}\nu _{0}^{2}}{3\epsilon mc^{3}}}={\frac {\gamma }{2\pi }}$

Con e, la carga del electrón y $\epsilon _{0}$ la permitividad eléctrica del vacío. Estos anchos son muchos menores a los que se encuentran normalmente en objetos astronómicos cuyas líneas espectrales has sido ensanchada por otros factores. Sin embargo, el ensanchamiento natural puede ser importante en algunos casos, como por ejemplo en espectroscopia láser

Figura (1) La línea adquiere un perfil Lorentziano

Donde $I_{0}$ es la máxima intensidad de radiación que alcanza la línea y $\nu _{0}$ es la frecuencia central de la línea.

Perfil de línea Lorentziano

La distribución Cauchy-Lorentz, llamada en honor a Augustin Cauchy y Hendrik Lorentz, es una distribución de probabilidad continua. Es conocida como la distribución de Cauchy y en el ámbito de la física se conoce como la distribución de Lorentz, la función Lorentziana ó la distribución de Breit-Wigner. Su importancia en la física es dada por ser la solución de la ecuación diferencial que describe la resonancia forzada. En espectroscopía describe la forma de las líneas espectrales que son ampliadas por diversos mecanismos, en particular, el mecanismo de ensanchamiento por colisión.

Función de densidad

En estadística la distribución de Cauchy (a veces también distribución de Lorentz) es una distribución de probabilidad continua cuya función de densidad es:

$f(x;0,1)={\frac {1}{\pi (1+x^{2})}}$

En general la distribución de Cauchy no tiene valor esperado ni varianza.

Sean U y V dos variables aleatorias uniformes dentro -1 y 1 y U2 + V2 < 1, entonces el número U / V tiene la distribución Cauchy

Perfil Lorentziano : Ensanchamiento o desplazamiento de la líneas espectrales por colisión de partículas emisoras o absorventes con otra partícula.

Un átomo excitado que decae espontáneamente a través de la transición 2 → 1, emite energía con frecuencia central $\omega _{0}={\frac {(E_{2}-E_{1})}{h^{-}}}$. Para obtener la distribución espectral que se origina en este proceso se describe al electrón excitado usando el modelo clásico del oscilador armónico amortiguado sin forzamiento de frecuencia ω, masa m, constante de restauración k y constante de amortiguamiento γ, donde esta última da cuenta de la energía radiada. En el caso de átomos reales el amortiguamiento es tan pequeño que $\gamma <<\omega$. De la mecánica clásica se tiene que la amplitud de oscilación x(t) se obtiene resolviendo la ecuación de movimiento:

$x^{..}+yx^{.}+\omega _{0}^{2}=0$

Donde $\omega _{0}^{2}=k/m.)$

Por lo tanto la solución de las ecuaciones anterior con condiciones x(0)= x 0 y x˙(0) = 0 es

$x(t)=x_{0}e^{-(\gamma /2)t}[cos(\omega t)+(\gamma /2\omega )sen(\omega t)]$

La frecuencia $\omega =(\omega _{0}^{2}-\gamma ^{2}/4)^{1/2}$ del oscilador amortiguado es ligeramente menor que la frecuencia $\omega _{0}$ del oscilador sin amortiguamiento. Sin embargo, para amortiguamientos pequeños γ << ω se puede realizar la aproximación $\omega \approx \omega _{0}$ y despreciar el segundo término. Con esta aproximación la solución queda:

$x(t)=x_{0}e^{-}(\gamma /2)t[cos(\omega _{0}t)$ ............... (3.1)

Figura 2: a) Oscilación amortiguada. b) Perfil de intensidad I(ω − ω0).

Debido a que la amplitud x(t) de la oscilación decrece gradualmente, la frecuencia de la radiación emitida deja de ser constante, mostrando una distribución A(ω).Figura (2)

Para encontrar la distribución de frecuencias se describe a la oscilación amortiguada x(t) como una superposición de oscilaciones monocromáticas exp(iωt) de frecuencia ω y amplitudes A(ω).

Para encontrar la distribución de frecuencias se describe a la oscilación amortiguada x(t) como una superposición de oscilaciones monocromáticas $e^{(i\omega t)}$ de frecuencia ω y amplitudes A(ω).

$x(t)={\frac {1}{2{\sqrt {2\pi }}}}\int \limits _{0}^{\infty }A(\omega )e^{(i\omega t)}d(\omega )$

Las amplitudes A(ω) se calculan usando la transformada de Fourier

$A(\omega )={\frac {1}{2{\sqrt {2\pi }}}}\int \limits _{-\infty }^{\infty }x(t)e^{(i\omega t)}d(t)$ .......... (3.2)

Dado que para t < 0, x(t) = 0 el límite de integración inferior puede igualarse a cero. Sustituyendo (3.1) en (3.2) e integrando se obtiene:

$A(\omega$ = ${\frac {x_{0}}{\sqrt {8\pi }}}({\frac {1}{i(\omega -\omega _{0})+(\gamma /2)}}+{\frac {1}{i(\omega +\omega _{0})+(\gamma /2)}})$ .............. (.3.3)

La intensidad real I(ω) ∝ $A(\omega )$ *$A(\omega )$ contiene términos con $(\omega )-(\omega _{0})$ y $(\omega )+(\omega _{0})$ en el denominador. Es posible encontrar una vecindad alrededor de la frecuencia central $(\omega _{0})$ de una transición atómica donde $(\omega +\omega _{0})2$ << $(\omega _{0}^{2})$, en ese intervalo los términos con $(\omega )+(\omega _{0})$ pueden ser despreciados obteniendo para el perfil de intensidad la expresión.

$I(\omega -\omega _{0})={\frac {C}{(\omega -\omega _{0})^{2}+(\gamma /2)^{2}}}$ ......... 3.4)

La constante C puede ser definida de dos maneras:

a) A fin de comparar diferentes perfiles de línea es útil definir un perfil de intensidad normalizado $I(\omega -\omega _{0})=I(\omega -\omega _{0})/I_{0}$ donde $I_{0}=\int I(\omega )d(\omega )$ tal que

$\int \limits _{0}^{\infty }L(\omega -\omega _{0})d\omega =\int \limits _{-\infty }^{\infty }L(\omega -\omega _{0})d(\omega -\omega )=1$ tal que

con esta normalización la integral de la ecuación(3.4) da como resultado

$C={\frac {I_{0}\gamma }{(2\pi )}}$

y se tiene

$L(\omega -\omega _{0})={\frac {1}{2\pi }}{\frac {\gamma }{(\omega -\omega _{0})^{2}+(\gamma /2)^{2}}}$

que es llamado el perfil Lorentziano normalizado. Su ancho de banda es ${\gamma }$

Cualquier distribución con un perfil Lorentziano es entonces de la forma

$I(\omega -\omega _{0})={\frac {I_{0}}{2\pi }}{\frac {\gamma }{(\omega -\omega _{0})^{2}+(\gamma /2)^{2}}}=I_{0}L(\omega -\omega _{0})$

cuyo máximo de intensidad es:

$I(\omega _{0})={\frac {2I_{0}}{\pi \gamma }}$

b) Frecuentemente la normalización de la ecuacion (3.4) es elegida de tal forma que $I(\omega _{0})=I_{0}$ En esta notación el perfil Lorentziano de una transicion |2| → |1| es:

$I(\omega )=I_{0}L*(\omega -\omega _{0})$ donde:

$L^{*}(\omega -\omega _{0})={\frac {(\gamma /2)^{2}}{(\omega -\omega _{0})^{2}+(\gamma /2)^{2}}}$

Haciendo el cambio de variable $x={\frac {(\omega _{0}-\omega )}{(\gamma /2}}$ se obtiene:

$L^{*}(\omega -\omega _{0})={\frac {1}{1+x^{2}}}$

con $L^{*}(\omega _{0})=1$

En esta notación la integral de I(ω) es

$\int \limits _{0}^{\infty }I(\omega )d\omega ={\frac {\gamma }{2}}\int \limits _{-\infty }^{\infty }I(x)dx=\pi I_{0}{\frac {\gamma }{2}}$

El perfil de Lorentz describe la forma de línea de una señal emitida por un sistema cuántico aislado, cuando éste decae deu n nivel excitado a un estado de menor energía

Ensanchamiento Doppler

Es la ampliación de las líneas espectrales debido al efecto Doppler causado por una distribución de velocidades de los átomos o moléculas. O también es el ensanchamiento de una línea espectral por la superposición de los desplazamientos aleatorios de los átomos emisores o absorbentes en estado gaseoso. Presentan forma gaussiana.

El ensanchamiento Doppler se produce especialmente en láseres de gas, como resultado del movimiento de las moléculas de gas. La longitud de onda de radiación emitida o absorbida por un átomo que se mueve con rapidez disminuye si el movimiento es hacia un transductor y se incrementa si el átomo se aleja del traductor. Este fenómeno se conoce como corrimiento o desplazamiento Doppler

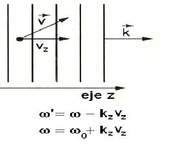
Considérese una onda electromagnética plana descrita por moviéndose en la dirección z del sistema de referencia de un observador en reposo, sea k = kz. Ahora colóquese un átomo en el estado base moviéndose a través de la onda con velocidad v = (vx, vy, vz) con respecto al mismo sistema. Por el efecto Doppler cualquier frecuencia ω en el sistema del observador sufre un corrimiento en el sistema coordenado centrado en el átomo, adquiriendo en este último el valor.

ω´$=\omega -k_{z}v_{z}$

Los átomos de la muestra sólo pueden absorber si la frecuencia ω coincide con la frecuencia central de absorción $\omega _{0}$. De lo anterior se sigue que la frecuencia de absorción $\omega =\omega _{a}$ es:

$\omega _{a}=\omega _{0}+k_{z}v_{z}$ ....... (4.1)

Para aquellos átomos cuya componente de velocidad vz se encuentra en la misma dirección del vector de propagación $k_{z}(k_{z}v_{z}>0)$ la frecuencia de absorción se incrementa.Figura 3)

En el caso contrario $(k_{z}v_{z}<0)$ la frecuencia de absorción disminuye.

Figura (3) Corrimiento Doppler de la frecuencia ω

La ecuación (4.1) puede reescribirse como

$\omega _{a}=\omega _{0}(1+{\frac {v_{z}}{c}})$ ............. (4.2)

Cuya diferencial es:

$d\omega ={\frac {\omega _{0}}{c}}dv_{z}$ ............. (4.3)

En equilibrio térmico, los átomos del gas siguen una distribución de velocidades Maxwelliana . A temperatura T, el número de átomos $n_{i}(v_{z})dv_{z}$ por unidad de volumen que se encuentran en el nivel Ei y cuya componente de velocidad z se encuentra entre $v_{z}$ y $vz+dv_{z}$ es:

$n_{i}(v_{z})={\frac {N_{i}}{V_{p}{\sqrt {\pi }}}}e^{(v_{z}/v_{p})^{2})}dv_{z}$ ........... (4.4)

Donde:

$N_{i}=\int n_{i}(v_{z})dv_{z}$ es la densidad de todos los átomos en el nivel $E_{i}$

$v_{p}=({\frac {2KT}{m}})^{2}$ es la velocidad más probable

m es la masa del átomo

k es la constante de Boltzmann

Sustituyendo $v_{z}$ y d$v_{z}$ de las ecuaciones (4.2) y (4.3) en la ecuación (4.4) obtenemos el número de átomos cuyas frecuencias de absorción fueron recorridas de la frecuencia $\omega _{0}$ dentro del intervalo comprendido entre $\omega _{0}$ y $\omega +d\omega$

$n_{i}(\omega )d\omega ={\frac {N_{i}c}{\omega _{o}V_{p}{\sqrt {\pi }}}}e^{-{\frac {c^{2}(\omega -\omega _{o})^{2}}{(\omega _{0}v_{p})^{2}}}}d\omega$ ............. (4.5)

Dado que la potencia absorbida $p(\omega )d\omega$ es proporcional a la densidad $n_{i}(\omega )d(\omega )$ de átomos que absorben en el intervalo dω, el perfil de intensidad de una línea espectral con ensanchamiento Doppler es:

$I(\omega )=I_{0}e^{-{\frac {c^{2}(\omega -\omega _{o})^{2}}{(\omega _{0}v_{p})^{2}}}}d\omega$ .......... (4.6)

Se obtiene un perfil Gaussiano con anchura

$(\gamma )D={\sqrt {ln2\omega _{0}v_{p}}}={\frac {\omega _{0}}{c}}{\sqrt {\frac {8KTln2}{m}}}$ ....... (4.7)

También conocido como ancho Doppler. Despejando ${\frac {\omega _{0}v_{p}}{c}}$ de (1.5) y usando la aproximación 1/(4ln2) = 0,36, la ecuación (1.5) se puede reescribir como:

$I(\omega )=I_{0}e^{-{\frac {(\omega -\omega _{o})^{2}}{(0.36\gamma ^{2}D)}}}$

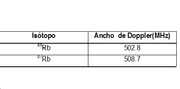
Introduciendo los valores del Rubidio en la ecuación (4.7) y tomando T = 290,15K se obtiene el ancho Doppler para cada isótopo, los cuales se presentan en la siguiente tabla A.

tabla A)

Un análisis más detallado muestra que una línea espectral con ensanchamiento Doppler no puede ser representada de manera estricta por un perfil puramente Gaussiano, como hasta el momento se ha trabajado, esto debido a que no todos los átomos con componente de velocidad vz bien definido absorben o emiten radiación a la misma frecuencia $\omega ^{,}=\omega _{0}(1+{\frac {v_{z}}{c}})$.

El tiempo de vida de los niveles atómicos origina que la respuesta en frecuencia de los átomos tenga un perfil Lorentziano centrado en la frecuencia on componente de velocidad vz bien definido absorben o emiten radiación a la misma frecuencia $\omega ^{,}$.

$L(\omega -\omega ^{,})={\frac {1}{2\pi }}{\frac {\gamma }{(\omega -\omega ^{,})^{2}+(\gamma /2)^{2}}}$ ............. (4.8)

Sea $n(\omega ^{,})d(\omega ^{,})=n(v_{z})dv_{z}$ el número de átomos por unidad de volumen cuya componente de velocidad z se encuentra en el intervalo $[v_{z},v_{z}+dv_{z}]$ . El espectro de distribución de intensidad $I(\omega )$ de la absorción o emisión total de todos los átomos en la transición $E_{1}$ → $E_{k}$ es:

$I(\omega -\omega ^{,})=I_{0}\int n(\omega ^{,})L(\omega -\omega ^{,})d\omega$ ........ (4.9)

Insertando las ecuaciones (4.5) y (4.8) en (4.9), se obtiene:

$I(\omega -\omega ^{,})=C\int {\frac {e^{-{\frac {c^{2}(\omega -\omega _{o})^{2}}{(\omega _{0}v_{p})^{2}}}}}{(\omega -\omega ^{,})^{2}+(\gamma /2)^{2}}}$

Con:

$C={\frac {\gamma N_{i}c}{2v_{p}(\pi )^{3/2}\omega }}$

Este perfil de intensidad es una convolución de los perfiles Lorentziano y Gaussiano, y es conocido como perfil de Voigt.

Figura 4: Perfil de Voigt.)

Aplicaiones Y Advertencias

Aplicación: En la astronomía y la física del plasma ,el ensanchamiento Doppler es una de las aplicaciones para la ampliación de las líneas espectrales,

Causas:

•Debido a la turbulencia del movimiento. Para una turbulencia completamente desarrollada, el perfil de la línea resultante es generalmente muy difíciles de distinguir de la térmica.

•Otra causa podría ser una amplia gama de velocidades macroscópicas como resultado, por ejemplo, de las porciones del retroceso y se acerca de una rápida rotación del disco de acreción .

Perfil de voigt

Woldemar Voigt (2 sept 1850 a 13 dic 1919) fue un alemán físico , que enseñó en la Universidad Georg August de Göttingen . Voigt finalmente pasó a la cabeza del Departamento de Física Matemática en Gotinga y fue sucedido en 1914 por Peter Debye , quien se hizo cargo del departamento teórico del Instituto de Física. En 1921, Debye fue sucedido por Max Born

En la espectroscopia, el perfil de Voigt (el nombre de Woldemar Voigt) es un perfil de la línea resultante de la convolución de dos mecanismos de ampliación, uno de los cuales solo se produce un perfil de Gauss (por lo general, como resultado de la ampliación Doppler), y el otro se producir un perfil de Lorentz. Todos los perfiles de línea normalizada pueden ser considerados como distribuciones de probabilidad. El perfil de Voigt es entonces una convolución de un perfil de Lorentz y un perfil de Gauss:

El perfil de Voigt, que describe con buena aproximación la forma de líneas espectrales de absorción emisión afectadas por mecanismos perturbadores externos naturaleza aleatoria, es conocido desde hace mucho tiempo. Inicialmente fue usado en astrofísica para determinar la temperatura de la atmósfera de las estrellas. La agitación caótica de los átomos emisores en el gas caliente que constituye atmósfera estelar hace que las líneas espectrales se ensanchen. Mediante la determinación de la magnitud de este ensanchamiento adicional, que se obtiene de la de convulsión del perfil de Voigt, se estima la temperatura que prevalece en una región dada de la atmósfera de la estrella.

Aunque se han considerado las diferentes contribuciones a la anchura de las líneas espectrales por separado, es obvio que en cualquier situación experimental varios efectos duraran por lo general, se actúa de forma simultánea. En consecuencia, la Líneas observadas no tendrá ni un simple Lorentziano o perfil gaussiano. Para investigar este se considera un átomo en movimiento, cuya frecuencia de resonancia es observar esta en $\omega _{0}^{,}$ Debido a la colisión o la vida útil de radiación finita la radiación emitida consiste en una distribución de frecuencias w acerca de la frecuencia $\omega _{0}^{,}$ central, que viene dado por la función de Lorentz

$L(\omega -\omega _{0}^{,})={\frac {\gamma /2\pi }{(\omega -\omega _{0}^{,})^{2}+\gamma ^{2}/4}}$

donde $\gamma$ es el ancho de la Distribución de intensidad media. el perfil espectral emitida por un conjunto de átomos en movimiento se obtiene promediando la ecuación anterior.

$I(\omega _{0}^{,}-\omega ,\gamma /\Delta )=\int \limits _{0}^{\infty }{\frac {\gamma /2\pi }{(\omega -\omega _{0}^{,})^{2}+\gamma ^{2}/4}}p(\omega _{o}^{,})d(\omega _{0}^{,})$

$=\int \limits _{0}^{\infty }{\frac {\gamma /2\pi }{(\omega -\omega _{0}^{,})^{2}+\gamma ^{2}/4}}{\frac {2}{\Delta {\sqrt {\pi }}}}e^{\frac {4(\omega _{0}^{,}-\omega _{0})^{2}}{\Delta ^{2}}}d(\omega _{0}^{,})$

El perfil de la línea resultante tiene la forma de un integrante de plegado de la Lorentziana y distribución gaussiano: Por lo tanto el perfil de una línea espectral Doppler ampliado está dada por la distribución de Gauss normalizada

$I(\omega _{0}^{,}-\omega ,\gamma /\Delta )=\int \limits _{0}^{\infty }v(\omega _{0}^{,}-\omega ,\Delta )L(\omega -\omega _{0}^{,},\gamma )d(\omega _{0}^{,})$

Que se conoce como el perfil de Voigt. la forma de este perfil se determina únicamente por la relación ${\frac {\gamma }{\Delta }}$ y en la fig B). Lorentziano, gaussiano, y el perfil de Voigt no se puede expresar en una analítica. Como nunca, se puede evaluar numéricamente y varias tabulaciones de esta función y relacionados han sido publicados, incluyendo en las de Davies y Vaughan (1963), fritos y Conte (1961) y Hummer (1965).

Tenemos y el perfil de la línea sería gaussiano a tres anchos de Doppler del centro de la línea antes de cambiar a la más lenta disminución de la forma Lorentziano. Para el caso contrario. ${\frac {\gamma }{\delta }}\ll 1$, el perfil sería de aproximadamente Lorentziano sobre las líneas de todo. cuando ${\frac {\gamma }{\delta }}\approx 1$, es posible determinar tanto el $\gamma$ y $\Delta$ a partir de una compartición detallada del perfil de la línea teórica y experimental.

Figura (6) Comparación de las formas de la distribución de Lorentz (L), el (G) distribución de Gauss, y la (V) línea de Voigt perfil para el que $\gamma =\Delta (ln2)^{1/2}$. perfiles se han normalizado a la intensidad máxima mismo y tienen la misma anchura media.

Un perfil de Voight describe la forma general de un línea espectral, incluidas las contribuciones tanto del Doppler y la amortiguación (naturales y colisiones / presión de la ampliación) perfiles. Ensanchamiento Doppler domina cerca de la longitud de onda central en el centro de la línea, mientras que los perfiles de amortiguación son más importantes en las alas (aproximadamente 1.8 x FWHM lejos del centro de la línea).