Optica: prismas

Prismas

Introducción

Vidrio prismático de sección triangular y transparente, que se utiliza para producir la reflexión, la refracción y la descomposición lumínica. La luz se descompone en sus colores primarios.

El índice de refracción: es una función de la longitud de onda por refracción de la luz a través del prisma a la mínima desviación. El haz o rayo de luz que emerge de un prisma esta más disperso que el incidente, con el fin de que la dispersión sea grande comparada con la anchura del haz se utiliza un haz muy estrecho. Además observamos que la luz incidente ya no es blanca, en su lugar se observa un espectro brillante de diversos colores los cuales tienen una determinada desviación, la que viene dada por el ángulo que forman las superficies a través de las cuales pasa la luz, por la dirección de incidencia en la primera cara y por el índice de refracción del prisma. De estas magnitudes, la única que puede diferir para los diferentes colores de la luz es el índice de refracción. Después de este análisis se deduce que las propiedades refringentes de una sustancia dependen del índice de refracción, podemos observar y demostrar experimentalmente que éste depende del color de la luz .

Conceptos

• Refracción: es el cambio de dirección de velocidad que experimenta una onda al pasar de un medio material a otro.

• Esparcimiento : Se refiere a lo granuloso o rugoso de un material.

• Difracción: es un fenómeno característico de las ondas, éste se basa en el curvado y esparcido de las ondas cuando encuentran un obstáculo o al atravesar una rendija.

• Reflexión: es el cambio de dirección de un rayo o una onda la cual ocurre en la superficie de separación entre dos medios, de tal forma que esta regresa al medio inicial

• Absorción: En electricidad, la permitividad, una constante física que describe cómo un campo eléctrico afecta y es afectado por un medio.

• Dispersión: fenómeno de separación de las ondas de distinta frecuencia al atravesar un material. Todos los medios materiales son más o menos dispersivos, y la dispersión afecta a todas las ondas; por ejemplo, a las ondas sonoras que se desplazan a través de la atmósfera, a las ondas de radio que atraviesan el espacio interestelar o a la luz que atraviesa el agua, el vidrio o el aire.

Tipos de prismas

• Prismas reflectivos: son los que únicamente reflejan la luz. Como son más fáciles de elaborar que los espejos, se utilizan en instrumentos ópticos como los prismáticos, los monoculares y otros.
• Prismas dispersivos: son usados para descomponer la luz en el espectro del arcoíris, porque el índice de refracción depende de la frecuencia(ver dispersión); la luz blanca entrando al prisma es una mezcla de diferentes frecuencias y cada una se desvía de manera diferente. La luz azul es disminuida a menor velocidad que la luz roja.
• Prismas polarizantes: separan cada haz de luz en componentes de variante polarización.

La ley de Snell

Dice que el producto del índice de refracción por el seno del ángulo de incidencia es constante para cualquier rayo de luz incidiendo sobre la superficie separatriz de dos medios \[ m\sin a=n\sin b \]

Dónde: Ángulos con respecto a la normal de la cara del prisma: incidente=a refractado=b

Índices de refracción del material: Externo al prisma= m Interno al prisma= n

Longitudes de onda emitidas por una fuente de luz

Para estudiar las longitudes de onda emitidas por una fuente de luz, en este caso luz de mercurio, se uso un espectrómetro de prisma (Fig. 1 y 2), el cual es usado comúnmente para estudiar las longitudes de onda emitidas por una fuente de luz. La luz emitida por la fuente pasa a través de una rendija angosta que se puede ajustar para generar un haz paralelo o colimado. La luz pasa a través del prisma donde se descompone en su espectro. Se utiliza el telescopio para observar la luz difractada. Nosotros podemos ver la imagen de la ranura a través del ocular del telescopio. Para poder observar varias de las imágenes formadas por las distintas longitudes de onda en sus diferentes ángulos de desviación, se gira ya sea el telescopio o el prisma. Observamos a través del telescopio la luz que entra donde se fija el ángulo 0° en circulo graduado. La luz pasa a través de un prisma donde se descompone en su espectro.

Figura 1. Telescopio

---

Se utiliza el lente del telescopio, que es usado como amplificador, para observar la luz refractada, se gira el telescopio hacia la izquierda hasta encontrar el espectro, luego giramos el prisma para buscar la desviación mínima. Nos ubicamos en cada línea espectral y medimos el ángulo para cada una en el círculo de Vernier que forma con el eje principal. Para lo cual existen datos experimentales para distintos prismas; de cristal de diferentes ángulos, prisma de plástico, y diferentes densidades colocadas en un prisma hueco; metanol, tetracloruro de carbono, agua, agua con sal, agua con azúcar.

---

Figura 2. Rayo de luz sobre un prisma

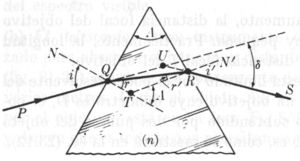
Rayo de luz incidente sobre un prisma

---

Ahora analizaremos cuando un rayo de luz incide sobre un prisma el cual es un medio limitado por dos superficies planas que forman un ángulo A. Suponemos que el medio tiene un índice de refracción n y que esta rodeado de un medio cuyo índice de refracción es la unidad, en este caso el aire. Sabiendo que el índice de refracción es diferente para las distintas longitudes de onda de la luz; debido a que n es función de la longitud de onda, la ley de Snell predice que una luz de diferente longitud de onda se desviara a distinto ángulo cuando incide sobre un material refractante. Se puede decir que los índices de refracción disminuyen al aumentar la longitud de onda, lo que implica que la luz azul se desviara más que la luz roja al pasar a través de un material refractante. Cualquier sustancia en la cual n varia con la longitud de onda se llama medio dispersor.

Un rayo que incide por la izquierda o sea PQ sufre dos difracciones y emerge desviándose de su dirección original de incidencia un ángulo llamado ángulo de desviación. Considerando en este caso una luz de Mercurio que incide sobre un prisma; los rayos que emergen en la segunda cara se abren en una serie de colores conocido como Espectro, estos colores en orden de longitud de onda decreciente son: rojo, naranja, amarillo, verde, azul y violeta. Gracias a Newton sabemos que cada uno de estos colores tiene un ángulo de desviación particular, que no es posible descomponer el espectro aun más y que los colores se pueden recombinar para formar la luz que incidió originalmente. Con el espectrómetro de prisma buscamos estudiar las longitudes de onda emitidas por la fuente de luz de Mercurio. Se puede observar el rayo incidente y el rayo emergente (Fig. 3)

Figura 3. Ondas

En la figura fácilmente se puede ver que valen las siguientes relaciones:

$\sin(i)=nsin(r)$ (1.0)

$\sin(i')=nsin(r')$ (1.1)

$\ (r)+(r')=A$ (1.2)

$\ =(i)+(i')-A$ (1.3)

La primera y segunda ecuación es la ley de Snell como ya se menciono, aplicada a las refracciones en Q y en R. La tercera se obtiene usando el triangulo QTP y la cuarta usando el triangulo QRU. Las tres primeras ecuaciones sirven para trazar el rayo, y la cuarta nos permite hallar la desviación.

Hay un rayo particular para el cual la desviación es mínima; se obtiene haciendo d/di = 0.De la ecuación (1.3) obtenemos:

$\ {\frac {d\delta }{di}}=1+{\frac {di'}{di}}$

Y para que d/di = 0 debemos tener:

$\ {\frac {di'}{di}}=-1$

De las ecuaciones (1.1) y (1.2) tenemos

$\ cos(i)(di)=ncos(r)(dr)$

$\ cos(i')(di')=ncos(r')(dr')$

$\ (dr)=-(dr')$

En consecuencia:

${\frac {di'}{di}}={\frac {cos(i)cos(r')}{cos(i')cos(r)}}$

Como los cuatro ángulos i, r, i' y r' son menores que y satisfacen las condiciones simétricas (1.0) y (1.1) se pueden satisfacer simultáneamente las ecuaciones (1.4) y (1.5) solamente si i = i' y r = r', para lo cual debe ser:

$I=1/2(min+A)r=1/2A$

Donde mín. es la desviación mínima. Nótese que en este caso el camino del rayo es simétrico respecto a las dos caras del prisma. Introduciendo la ecuación (1.6) en la ecuación (1.0) obtenemos

$n={\frac {sin1/2(\delta ..+A)}{sin1/2A}}$

Que es una formula conveniente para medir el índice de refracción de una sustancia, hallando mín. experimentalmente en un prisma de ángulo A conocido.

Experimentalmente se logra obtener variados n. Los datos fueron son los siguientes

líneas espectrales

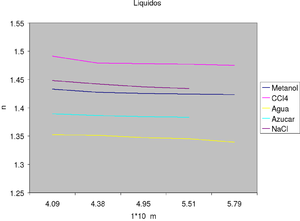
En las observaciones nos percatamos que solo se distinguen tres líneas espectrales comunes para ambas soluciones; Naranja, Amarillo, Azul. También nos podemos dar cuenta que la que mayor disperse es la línea azul clara por su pendiente nos percatamos fácilmente, y la que mayor disperse es la línea amarilla.

A continuación se muestra un gráfico que relaciona todos las mediciones realizadas con distintos compuestos (líquidos transparentes) El grafico relaciona los índices de refracción versus las longitudes de onda de cada línea espectral.

líneas de refracción versus

Como hemos podido observar una onda que se refracta en un medio dispersivo cuyo índice de difracción depende de la frecuencia, el ángulo de refracción también depende de la frecuencia o de la longitud de onda. Como la luz incidente no es monocromática, o sea se compone de varias frecuencias o longitudes de ondas superpuestas, cada onda se refracta con un ángulo diferente; este fenómeno se llama dispersión. Observamos que en el prisma este fenómeno es mucho más notorio, especialmente en los bordes. La dispersión de un prisma se define por:

$D={\frac {d\delta }{d\Lambda }}={\frac {d\delta }{dn}}{\frac {dn}{d\Lambda }}$

El factor d/dn depende fundamentalmente de la geometría del sistema, en cambio el factor d/d depende del material del que esta compuesto el prisma. Derivando las ecuaciones (1.0) a (1.3), con respecto al índice de refracción n encontramos que:

$\ dr/dn+dr'/dn=0$

$\ d\delta /dn=di'/dn$

$\ cosi'{\frac {di'}{dn}}=senr'+ncosr'{\frac {dr'}{dn}}$

$\ 0=sinr+ncosrdr/dn$

Si combinamos estos cuatro resultados y utilizamos la ecuación(1.2), obtenemos finalmente:

$\ {\frac {d\delta }{dn}}={\frac {di'}{dn}}={\frac {sinA}{cos(i')cos(r)}}$

Si se orienta el prisma para obtener desviación mínima, tenemos:

${\frac {d\delta }{dn}}={\frac {2sin1/2A}{cos1/2(\delta ...+1/2)}}$

El segundo factor dn/d en la ecuación (1.8) depende de la naturaleza de las ondas y del medio. Para las ondas electromagnéticas en general y para la luz en particular, una expresión aproximada y satisfactoria para el índice de refracción en función de la longitud de onda esta dada por la formula de Cauchy

$n=A+{\frac {B}{\Lambda ^{2}}}$

${\frac {dn}{d\Lambda }}={\frac {2B}{\Lambda ^{3}}}$

Donde A y B son constantes características de cada sustancia como mostramos en los gráficos anteriores, la variación de n con respecto a para diversos materiales y líquidos transparentes. De la ecuación (1.9) obtenemos: La dispersión en un prisma es entonces:

$D={\frac {d\delta }{d\Lambda }}={\frac {2sin1/2A}{cos1/2(\delta ...+A)}}{\frac {-2B}{\Lambda ^{3}}}$

El signo negativo significa que disminuye cuando la longitud de onda aumenta, de modo que el rojo se desvía menos que el violeta. Logramos confirmar que cuando el cambio de dirección de la luz es mayor, el índice de refracción del medio también lo es lo que concuerda con la ley de Snell. Del gráfico observamos que los índices de refracción para cada material varia según la línea espectral en que fue medida, además que este no tiene una mayor variación Después de hacer las medicines nos percatamos de que el prisma tiene la desventaja sobre la red de difracción ya que de este solo depende de su geometría, en cambio el prisma depende de las propiedades dispersivas del material.

Conclusiones

---

A lo largo de toda esta investigación creo que mi objetivo lo pude llevar a cabo; el cual era tener el conocimiento de un prisma óptico y todo con respecto al tema, en este caso los tipos de prisma y más que ello saber cómo se utiliza este tipo de material, que a lo largo de nuestra trayectoria como estudiantes universitarios nos será de ayuda en otras ocasiones. Un prisma es un vidrio prismático de sección triangular y transparente, que se utiliza para producir la reflexión, la refracción y la descomposición lumínica. Existen tres tipos de prismas que son: Los prismas reflectivos, los prismas dispersivos, los prismas polarizantes, para poder entender este tema es de suma importancia saber acerca de de La ley de Snell, que es de lo que se habla en un prisma esta nos dice que el producto del índice de refracción por el seno del ángulo de incidencia es constante para cualquier rayo de luz incidiendo sobre la superficie separatriz de dos medios Cabe mencionar que el prisma óptico fue utilizado sistemáticamente por Isaac Newton en la construcción de su teoría de los colores, según la cual la luz blanca es la superposición de luz de siete colores diferentes, rojo, anaranjado, amarillo, verde, azul, añil y violeta. Experimentos concienzudos realizados con rayos de luz solar y prismas ópticos permitieron a Newton llegar no sólo a demostrar el carácter compuesto de la luz blanca, sino a explicar el fenómeno de la dispersión cromática óptica.

Referencias

---

---

Aportación por Usuario: REYNA 05:15 4 dic 2011 (UTC)

---