Ondas: tipos de
En el movimiento ondulatorio la energía y el ímpetu se mueven de un lugar a otro sin que las partículas materiales viajen, es decir, puede considerarse como un transporte de energía y cantidad de movimiento desde un punto del espacio a otro sin transportar materia, la energía y el movimiento se transportan mediante una perturbación en el medio que se propaga en el mismo.
Las ondas pueden clasificarse como uni, bi, o tridimensionales, de acuerdo con el número de dimensiones en que se propaguen la energía, igualmente puede clasificarse de acuerdo al movimiento de las partículas del medio y la propagación de la onda.
Ondas mecánicas
Las ondas mecánicas son aquellas que se desplazan a través de un medio material deformable o elástico. Podemos clasificar las ondas mecánicas considerando la dirección del movimiento de las partículas, con respecto a la dirección de propagación de la onda.
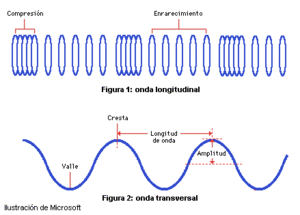
Ondas transversales. Esta es una onda unidimensional en la cual el movimiento de las partículas es perpendicular a la dirección de propagación de la onda, si agitas un extremo libre de una cuerda hacia arriba y hacia abajo, el movimiento de la cuerda es perpendicular a la dirección del movimiento de la onda. Las ondas que se producen en las cuerdas tensas de los instrumentos musicales y en las superficies de los líquidos son transversales así como la luz.
Ondas Longitudinales. Las ondas longitudinales también son ondas unidimensionales en las que el movimiento de la onda es un vaivén a lo largo de la dirección de propagación, la perturbación es paralela a la dirección de propagación. Cuando un resorte en tensión se perturba generando una oscilación desde uno de los extremos, las partículas vibran paralelas a la dirección en la que viaja la onda. El sonido se compone de ondas longitudinales.
Existen ondas que no son completamente transversales ni longitudinales si no una combinación de ambas son ondas bidimensionales, como las ondas superficiales o rizos de agua que se forman al arrojar una piedra a un estanque tranquilo, las partículas se mueven perpendicularmente pero también se desplazan paralelas a la perturbación.
Mas sobre ondas mecánicas Ondas: mecanicas
Onda Armónica
Si se produce una pulsación que viaje por una cuerda estirada aplicándole un solo movimiento lateral en su extremo. Cada partícula permanece en reposo hasta que la pulsación llega hasta ella, luego se mueve durante un tiempo corto y luego permanece nuevamente en reposo. Si continuamos moviendo el extremo de la cuerda en vaivén constante produciremos un tren de ondas que viaja a lo largo de la cuerda. Si la perturbación es periódica produciremos un tren de ondas periódico, donde cada partícula de la cuerda tendría un movimiento periódico. El caso especial más sencillo es una onda armónica, donde cada partícula experimenta un movimiento armónico simple. Realmente existen un gran numero de sistemas mecánicos en donde se producen vibraciones puramente sinusoidales, siendo originadas por fuerzas restauradoras que son proporcionales a los desplazamientos respecto al equilibrio. En este tipo de ondas la ecuación de movimiento de un cuerpo de masa m sujeto a un muelle, está dada por:
\begin{equation} m \frac{d^2 y}{dx^2}\ =-kx \label{1} \end{equation}
El movimiento armónico simple es un caso particular del movimiento sinusoidal, así una solución de la ecuación (\ref{1}) se puede escribir como:
Que se puede expresar como:
Donde A es la amplitud y generalmente se expresa como, , entonces escribimos.
\begin{equation} x(t)=A \sin\left(\omega t +\rho\right ) \label{2} \end{equation}
Esta es una expresión mas conocida y se conoce como constante de fase, si aumentamos $2\pi$ en el argumento de la ecuación anterior corresponde precisamente al periodo, así se observa:
Donde T es el periodo, ahora en un t=0 y , la ecuación (\ref{2}) se reduce a:
\begin{equation} x_0=A \sin\left(\rho_0\right ) \label{3} \end{equation}
Derivando la ecuación (\ref{2}),
Aplicando las condiciones iniciales.
\begin{equation} v_0=\frac{dx(0)}{dt}=\omega A\cos\rho \label{4} \end{equation}
De las ecuaciones (\ref{3}) y (\ref{4}), se obtiene;
De esta forma encontramos dos resultados importante en las ondas mecánicas armónicas, la amplitud y la contante de fase en termino de posición y velocidad inicial.
Las ondas de sonido y de luz (ondas electromagnéticas) que viajan radialmente partiendo de una pequeña fuente son tridimensionales.
Ondas electromagnéticas
Lo único que hace diferente una onda electromagnética de otra es su longitud ó frecuencia de onda, en el espectro electromagnético se clasifican las longitudes de estas ondas en intervalos, generalmente estos intervalos reciben nombres como:
Rayos Gamma. Estos rayos tienen una longitud de onda del orden de m, o menores. Los rayos gamma son ondas electromagnéticas de gran energía, se producen a causa de radiaciones nucleares causadas por la desintegración de isótopos radiactivos, es decir, son transiciones nucleares como cuando ocurre una desintegración de partículas beta.
Rayos X. Tienen una longitud de onda de entre 10 a 0.1 nanómetros, surgen por la desaceleración de electrones, o partículas cargadas. Estas radiaciones tienen gran importantes en los diagnósticos médicos, ya que pueden penetrar fácilmente el tejido del blando del cuerpo pero se detienen en la materia solida como los huesos.
Ultravioleta. Con longitudes de onda entre 1nm y 400nm se producen en las transiciones de electrones libres como las que parten de fuentes térmicas como el sol.
Luz Visible. Tiene una longitud de onda entre 400nm y 700nm. Esta luz frecuentemente se emite en transiciones ópticas, estas ocurren cuando los electrones externos cambian su estado de movimiento. El sol tiene sus niveles máximos de radiación en este mismo intervalo, es por esto que los ojos se han adaptado para ser sensibles a estas radiaciones.
Infrarrojo. Las longitudes de onda del infrarrojo son aproximadamente de 700nm a 1mm, se emite cuando los átomos cambian su movimiento vibratorio o rotatorio, se manifiesta como un cambio de energía interna, por esto la radiación infrarroja es importante en la transferencia de calor, es por esto que también es conocida como radiación térmica.
Microondas. También son conocidas como ondas de radio cortas con longitudes de onda entre 1mm y 1m, se generan en los osciladores electromagnéticos de circuitos eléctricos. Ondas de Radio. Con longitudes de onda mayores a 1m, se producen en electrones en una fuente terrestre que oscilan en conductores de circuitos eléctricos.
Una solución de la ecuación de onda electromagnética.
Entonces de acuerdo a la clasificación anterior las ondas electromagnéticas se originan a partir del movimiento de las cargas, pero si no tomamos en cuenta las causas que origina estos movimientos y utilizando las leyes de la electricidad y el magnetismo, se deduce la existencia de los campos eléctricos y magnéticos por lo tanto una ecuación de onda que describe la propagación por el espacio libre de cargas y corrientes es la ecuación de onda plana donde se supone también que, el campo magnético B, depende del tiempo así como el campo eléctrico E, también supondremos que las magnitudes de los campos son constantes.
Recordemos las ecuaciones de Maxwell con las cuales definiéremos los campos magnéticos y eléctricos.
Las ecuaciones de Maxwell cuando no existen fuentes, es decir cuando el medio está libre de cargas q y corriente I, se reducen como:
\begin{equation} \oint_S EdA=0 \label{1a} \end{equation}
\begin{equation}
\oint_S BdA=0
\label{2a}
\end{equation}
\begin{equation}
\oint_C Edl=-\frac{d}{dt} \int_S BdA
\label{3a}
\end{equation}
\begin{equation}
\oint_C Bdl= \mu_0 \epsilon_0\frac{d}{dt} \int_S EdA
\label{4a}
\end{equation}
Usando las ecuaciones (\ref{3a}) y (\ref{4a}), podemos relacionar los campos magnéticos y eléctricos entre sí, tomando la componente del campo eléctrico y además , entonces.
\begin{equation} \oint_C Edl=E_y (x_2)\Delta y -E_y (x_1)\Delta y \label{5a} \end{equation}
Donde, es el valor que toma el campo eléctrico evaluado en . Si el campo eléctrico solo depende la posición en , suponemos que Δx es muy pequeño, de tal forma que.
\begin{equation} E_y (x_2)-E_y(x_1)=\Delta E_y\approx \frac{\delta E_y}{\delta x}\Delta x \label{6a} \end{equation}
Sustituyendo la ecuación (\ref{6a}) en (\ref{5a}), obtenemos.
\begin{equation} \oint_C Edl =\Delta x\Delta y\frac{\partial E_y}{\partial x} \label{7a} \end{equation}
Así el flujo de inducción magnética (ver ecuación 2) que atraviesa el área ΔxΔy, es por un lado.
\begin{equation} \oint_S BdA=B_z\Delta x\Delta y \label{8a} \end{equation}
Sustituyendo la ecuación (\ref{8a}) y (\ref{7a}) en la ley de Faraday ecuación (\ref{3a}),
\begin{equation}
\frac{\partial E_y}{\partial x}=-\frac{dB_z}{dt}
\label{9a}
\end{equation}
De esta última expresión podemos observar que existe una componente z en el campo magnético para cada componente y del campo eléctrico, es decir existe un campo de inducción magnética que depende del tiempo mientras que el campo eléctrico depende de x, así mismo debe existir un campo de inducción magnética dependiente de la posición x y un campo eléctrico dependiente del tiempo.
Si partimos de la ecuación (\ref{4a}) y seguimos un procedimiento análogo al que nos llevo a la ecuación (\ref{9a}), obtenemos una relación en la cual el campo magnético depende solamente de la posición y el campo eléctrico del tiempo.
\begin{equation} \oint_C Bdl=B_z (x_2)\Delta z -B_z (x_1)\Delta z =\Delta x\Delta y\frac{\partial B_z}{\partial x} \label{10a} \end{equation}
Por otro lado de la ecuación (\ref{1a}).
\begin{equation} \oint_S EdA=E_y\Delta x\Delta z \label{11a} \end{equation}
Sustituyendo (\ref{10a}) y (\ref{11a}) en la ecuación (\ref{4a}).
\begin{equation} \frac{\partial B_z}{\partial x}=\mu_0\epsilon_0\frac{dE_y}{dt} \label{12a} \end{equation}
Ahora las ecuaciones (\ref{9a}) y (\ref{12a}) podemos escribirlas como.
\begin{equation} \frac{\partial^2 E_y}{\partial x^2}=\mu_0\epsilon_0\frac{\partial^2 B_z}{\partial t \partial x} \label{13a} \end{equation}
\begin{equation} \frac{\partial^2 B_z}{\partial x^2}=\mu_0\epsilon_0\frac{\partial^2 E_y}{\partial t \partial x} \label{14a} \end{equation}
Entonces sustituyendo (\ref{9a}) y (\ref{12a}) respectivamente, y recordando que .
\begin{equation} \frac{\partial^2 E_y}{\partial x^2}=\frac{1}{c^2}\frac{\partial^2 E_y}{\partial t^2} \label{15a} \end{equation}
\begin{equation}
\frac{\partial^2 B_z}{\partial x^2}=\frac{1}{c^2}\frac{\partial^2 B_z}{\partial t^2}
\label{16a}
\end{equation}
Solución para una onda electromagnética plana armónica.
Para la componente y del campo eléctrico , proponemos un solución para la ecuación (\ref{15a}) de la forma, , sustituyendo en la ecuación diferencial parcial (\ref{16a}) obtenemos.
Así es sencillo encontrar una solución para $T(t)$ y $X(x)$.
Al sustituir en , haciendo un poco de álgebra :
\begin{equation} E_y(x,t)=a_1 a_2 \cos\left(\omega t\right)\cos\left(kx\right)+a_1 n_2 \cos\left(kx\right)\sin\left(\omega t\right)+n_1 a_2 \cos\left(\omega t\right)\sin\left(ky\right)+n_1 n_2 \sin\left(ky\right)\sin\left(\omega t\right) \label{17a} \end{equation}
Podemos usar identidades trigonométricas para reducir la ultima expresión, por ejemplo para.
Entonces la expresión (\ref{17a}) puede escribirse como.
Donde:
Entonces.
\begin{equation} E_x = {E_1x} + {E_2x} \end{equation}
Proponemos una solución de la forma,
Por lo tanto sustituyendo en la ecuación (\ref{16a}).
Entonces tendremos las solución general para $X(x)$ y $T(t)$, recordando que:
entonces si.
donde:
Si consideramos la soluciones y, evaluamos en ambas ecuaciones en y .
En otro instante , , con ,, de tal forma que:
De la relación anterior concluimos.
\begin{equation}
\Delta t=\frac{\Delta x}{c}
\end{equation}
Mas sobre ondas electromagnéticas Ondas EM
Frente de Onda
Imaginemos una piedra lanzada a un lago tranquilo . Los rizos circulares se esparcen hacia afuera desde el punto en que la piedra entro al agua figura 2. A lo largo de un rizo circular dado, todos los puntos están en el mismo estado de movimiento. Esos puntos definen una superficie llamada frente de onda. Si el medio es de densidad uniforme, la dirección del movimiento de las ondas esta en angulo recto al frente de la onda. Una linea normal a los frentes de onda, que indique la dirección del movimiento de las ondas, se llama rayo.
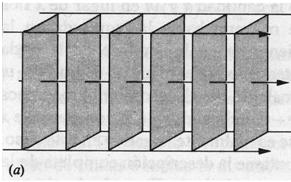
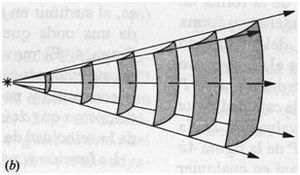
Los frentes de onda pueden tener muchas formas. Una fuente central en la superficie del agua produce ondas bidimensionales con frentes de onda circulares y rayos que salen hacia afuera a partir del punto de la perturbación figura 2. En cambio, un palo muy largo arrojado horizontalmente al gua produciría cerca de su centro perturbaciones que viajan como lineas rectas, y cuyos rayos serían líneas paralelas. la analogía tridimensional, en la cual las perturbaciones viajan en una sola dirección, es la onda plana. En un instante dado, las condiciones son las mismas en todas partes de cualquier plano perpendicular a la dirección de propagación. Los frentes de onda son planos, y los rayos son líneas rectas paralelas figura 3. La analogía tridimensional de las ondas circulares son las ondas esféricas. Aquí, la perturbación se propaga hacia afuera en todas direcciones desde una fuente puntal de ondas. Los frentes de onda son esferas, y los rayos son líneas radiales que salen de la fuente puntual en todas direcciones figura 4. Lejos de esta fuente los frentes de onda esféricos tienen una curvatura muy pequeña, y dentro de una región limitada pueden considerarse a menudo como planos. Por supuesto, existen otras muchas formas de frentes de onda posibles.
Se ve claramente como en la figura 3 representan frentes de onda espaciados en una longitud de onda , las flechas representan rayos y en la figura 4 representa una onda esférica en donde los frentes de onda, espaciados en una longitud de onda, son superficies esféricas y los rayos están en dirección radial.
Véase También
- Ondas: mecanicas
- Ondas: ecuacion de onda
- Ondas Mecanicas Longitudinales
- Ondas: ondas longitudinales
- Ondas EM
Referencias
S. Burbano de Ercilla, Fisica General Tomo II. 32a. ed. ALFAOMEGA, 2006
Eliezer Braun, Física 2: Electricidad y Magnetismo. 1er. ed. Trillas 1993
Anthony French, Vibraciones y Ondas. 1er. ed. Reverté 1991
Paul Tipler, Física Tomo II. 3er. ed. Reverte 1994
Robert Resnick, Física Parte II. 1er. ed. Compañía editorial continental. 1970
Robert Resnick, Física Tomo II. 4ta. ed. Compañía editorial continental. 1996
Aportación de: Aurora Gonzalez 16:05 30 mar 2012 (UTC)