Ondas: esfericas
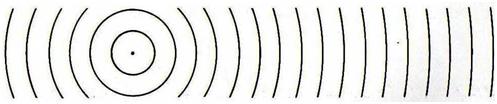
Arrojemos una piedra a un deposito de agua. Las ondas superficiales que proceden del punto de impacto, se esparcen hacia afuera en ondas circulares bidimensionales. Extendiendo esta imagen a tres dimensiones, imagínese una pequeña esfera que late, rodeada de un fluido. La contracción y expansión de la fuente generan variaciones de presión que se propagan hacia afuera como ondas esféricas.
Considérese ahora una fuente puntual ideal de luz. La radiación que procede de ella fluye radialmente hacia afuera, uniformemente en todas las direcciones.Se dice que la fuente es isótropa y los frentes de onda resultantes son de nuevo esferas concéntricas con diámetro creciente cuando se expanden en el espacio que los rodea. La simetría obvia de los frentes de onda sugiere que podría ser más conveniente describirlos matemáticamente en términos de coordenadas esféricas polares.
En esta representación, el operador Laplaciano es
\begin{equation}
\nabla^{2}=\frac{1}{r^{2}}\frac{\partial}{\partial{r}}(r^{2}\frac{\partial}{\partial{r}})+\frac{1}{r^{2}\sin\theta}\frac{\partial}{\partial{\theta}}(\sin\theta\frac{\partial}{\partial{\theta}})+\frac{1}{r^{2}\sin^{2}\theta}\frac{\partial^{2}}{\partial{\phi^{2}}}
\label{1}
\end{equation}
Donde se definen por
Recuerdese que estamos buscando una descripción de ondas esféricas, ondas que son simétricas esféricamente (es decir, que no dependen de ni de ); por lo tanto
\begin{equation} \psi(\mathbf{r})=\psi(r,\theta,\phi)=\psi(r) \label{2} \end{equation}
Entonces el Laplaciano de es simplemente
\begin{equation} \nabla^{2}\psi(r)=\frac{1}{r^{2}}\frac{\partial}{\partial{r}}(r^{2}\frac{\partial{\psi}}{\partial{r}}) \label{3} \end{equation}
Este resultado se puede obtener sin conocer la ecuación (\ref{1}).
Comience con la forma cartesiana del Laplaciano, ecuación 7 del tema Ondas en 3 dimensiones y opere sobre la función de onda simétricamente esférica y convierta cada término en coordenadas polares.
Examinando solamente la dependencia de x, tenemos
y
ya que
Utilizando
Tenemos
y
Ahora teniendo , formamos y y sumando obtenemos
La cual es equivalente a la ecuación (\ref{2}) este resultado puede expresarse
\begin{equation} \nabla^{2}\psi=\frac{1}{r}\frac{\partial^{2}}{\partial{r^{2}}}(r\psi) \label{4} \end{equation}
La ecuación diferencial de onda puede escribirse como
\begin{equation} \frac{1}{r}\frac{\partial^{2}}{\partial{r^{2}}}(r\psi)=\frac{1}{v^{2}}\frac{\partial^{2}\psi}{\partial{t^{2}}} \label{5} \end{equation}
Multiplicando ambos lados por r,obtenemos
\begin{equation} \frac{\partial^{2}}{\partial{r^{2}}}(r\psi)=\frac{1}{v^{2}}\frac{\partial^{2}}{\partial{t^{2}}}(r\psi) \label{6} \end{equation}
Obsérvese que esta expresión es ahora precisamente la ecuación diferencial de onda unidimensional, ecuación 6 del tema ondas: ecuación de onda, donde la variable espacial es r y la función de onda es el producto . La solución de la ecuación 6 es entonces
o
Esto representa una onda esférica que progresa radialmente hacia afuera desde su origen, con una velocidad constante v, y que tiene una forma funcional arbitraria f. Otra solución está dada por
Y en este caso la onda esta convergiendo hacia el origen. El hecho de que esta expresión falla en r=0 es de poca importancia práctica
Un caso especial de la solución general
es la onda esférica armónica
o
Donde la constante A se denomina intensidad de la fuente.Para cualquier valor fijo del tiempo, esto representa una agrupación de esferas concéntricas que llenan todo el espacio. Cada frente de onda, o superficie de fase constante, está dado por kr=constante
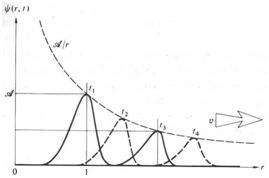
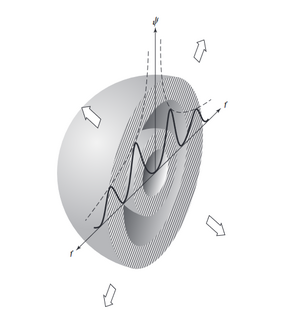
Obsérvese que la amplitud de cualquier onda esférica es una función de r, donde el término sirve como factor de atenuación. Contrariamente a la onda plana, una onda esférica disminuye en amplitud, cambiando por lo tanto su perfil, al expandirse y alejarse del origen la figura 2 ilustra este hecho gráficamente, mostrando una exposición múltiple de un pulso esférico en cuatro tiempos diferentes. El pulso tiene la misma extensión en el espacio en cualquier punto a lo largo de cualquier radio r, es decir, el ancho del pulso a lo largo del eje r es una constante. la figura 3 es un intento de relacionar la representación de , de la figura anterior con su forma real de onda esférica. Representa la mitad de un pulso esférico en dos tiempos diferentes, cuando la onda se expande hacia afuera. Recuérdese que estos resultados se obtienen independientemente de la dirección de r, debido a la simetría esférica. Podríamos también haber dibujado una onda simétrica, en lugar de un pulso, en las figuras 2 y 3 . En este caso, la perturbación sinusoidal habría estado limitada por las curvas
y
La onda esférica saliente que procede de una fuente puntual y la entrante que converge hacia un punto, son idealizaciones. En realidad, la luz sólo se aproxima a ondas esféricas como también sólo se aproxima a ondas planas.
Cuando un frente de onda esférico se propaga hacia afuera, su radio aumenta. A una distancia suficiente de la fuente, una pequeña área del frente de onda se parecerá mucho a una porción de onda plana. Véase ondas: planas