Imagenologia por resonancia magnetica nuclear
Introducción
La imagenología por resonancia magnética nuclear es una poderosa técnica para el diagnóstico médico y la planeación prequirurgica, basada en el fenómeno de resonancia magnética nuclear (NMR). El fenómeno de la resonancia magnética nuclear comienza en 1924 cuando Pauli demuestra una estructura hiperfina en el espectro atómico; posteriormente, en 1946, por Bloch y Purcell miden el fenómeno de resonancia magnética, sin embargo, ellos trabajan en análisis espectroscópicos y fue hasta 1973 cuando Paul Lauterbur y Peter Mansfiel proponen usarlo para imagen como diagnóstico médico. Es una técnica segura, pues no se necesita exponer al paciente a radiación ionizante, como los rayos-X.
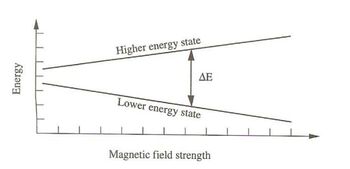
Algunos núcleos atómicos tienen la característica que cuando son colocados en un campo magnético estático, éstos asumirán alguno de los estados: el de mayor energía o el de menor energía. La diferencia de energía que existe entre estos dos estados es linealmente proporcional a la fuerza del campo magnético aplicado, esto es conocido como el efecto Zeeman.
En el estado de equilibrio térmico, el número de núcleos en el estado de mayor energía será ligeramente menor que en el de menor energía. Los núcleos pueden saltar del estado de mayor energía al de menor o del de menor al de mayor energía emitiendo o absorbiendo, respectivamente, un fotón de energía igual a la diferencia entre los dos estados. Si irradiamos núcleos con ondas electromagnéticas, generadas por una sonda de radiofrecuencia, a determinada frecuencia, algunos núcleos del estado de menor energía, absorberán la energía de los fotones y saltarán al estado de mayor energía, rompiendo así el equilibrio térmico, sin embargo, debido a el exceso de núcleos en el estado, algunos tenderán a regresar al estado de menor energía, para intentar recuperar el equilibrio térmico, emitiendo ondas electromagnéticas, las cuales podrán ser detectadas con una sonda de radiofrecuencia. Las señales de NMR recibidas por la sonda de RF pueden ser analizadas para estudiar las propiedades del núcleo y su entorno.
Principios físicos de la resonancia magnética nuclear
Spin
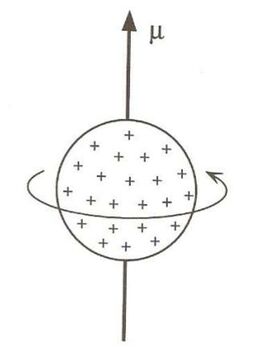
Se ha demostrado que ciertos núcleos poseen una propiedad conocida como spin. Pensemos en un protón como una pequeña esfera que contiene carga positiva distribuida uniformemente, la cual rota a gran velocidad sobre su eje, por lo tanto, la carga neta estará circulando sobre el eje de rotación, esta corriente producirá un pequeño campo magnético, llamado "momento magnético", simbolizado por $\boldsymbol{\mu}$. Además, debido a que el protón poseé una masa, la rotación producirá un momento angular. Con los neutrones y electrones, ocurre algo similar. La relación que exite entre el momento angular y el momento magnético de un núcleo, esta dada por: \begin{equation} \boldsymbol{\mu}=\gamma\textbf{J} \label{mommag} \end{equation} donde $\gamma$ es una constante de proporcionalidad llamada constante giromagnética, característica del núcleo y $\textbf{J}$ ES EL MOMENTO MAGNÉTICO DEL NÚCLEO.
Ahora consideremos un sistema aislado con 2 dos protones, habrá dos posibles configuraciones para el momento angular, y por lo tanto para el momento magnético de cada protón. Pueden estar alineados en el mismo sentido, lo cual resultaría en una configuración de mayor energía, o en sentidos opuestos, lo que sería un estado de menor energía, siendo esta, la configuración más estable; en dicha configuración se produciría un momento neto igual a cero y no se crearía momento magnético. Los núcleos que cumplen con la condición anterior, no son de interés para NMR porque no interaccionan fuertemente con los campos magnéticos.
En núcleos con un número impar de protones o de neutrones, es imposible tener momento angular neto igual a cero, dichos núcleos se dice que tienen spin nuclear. Estos núcleos son de gran importancia para la NMR, entre ellos se incluye el $^1H$, el cual será el núcleo más importante por su gran concentración natural en el cuerpo. En NMR estamos interesados en hacer "resonar" el núcleo entre los estados de energía por la aplicación de un campo magnético externo.
Comportamiento de los núcleos en un campo magnético externo
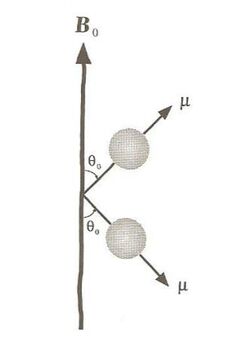
Ahora consideremos a un protón aislado, el cual está sometido en un campo magnético uniforme, $B_0$. El protón asumirá alguno de los dos estados de equilibrio, ya sea el estado paralelo, i.e. con su componente $z$ del momento magnético alineada con el campo externo $B_0$, o el estado antiparalelo, i.e., con su componente $z$ opuesta al campo magnético; ambos estados son estables, sin embargo la energía asociada al primer estado será menor que la del segundo.
Los valores de $\mu$ y su componente en $z$, $\mu_z$, están dados por la mecánica cuántica como [1] \begin{equation} \mu=\frac{\gamma h \sqrt{3}}{4\pi} \label{mu} \end{equation} \begin{equation} \mu_z=\frac{\gamma h}{4\pi} \label{mu-z} \end{equation} donde $h=6.629x10^{-34}$ $J$$\cdot{s}$, es la constante de Planck's.
De la figura anterior, podemos encontrar el \ángulo $theta_0$ de la siguiente manera \begin{equation} \cos \theta_0 = \frac{\mu_z}{\mu} \label{coseno} \end{equation}
Entonces, el ángulo $\theta_0$ entre la componente $z$ del vector $\mu$ y el eje $z$ (dirección de $B_0$), está dado por \begin{equation} \theta_0=\arccos(\frac{\mu_z}{\mu})=\arccos(\frac{1}{\sqrt{3}})\approx 54.7^{\circ} \label{angulo} \end{equation}
La diferencia de energía entre los dos estados, se puede conocer gracias al efecto Zeeman, de la mecánica cuántica [2] \begin{equation} \Delta E=2\mu B_0 \label{delta} \end{equation}
El fotón que se emita o se absorba al cambiar de estado, tendrá una energía $\Delta E$ y frecuencia $\nu$, las cuales están relacionadas por \begin{equation} \Delta E= h\nu \label{delta2} \end{equation} de la Eq.(\ref{delta}) y Eq.(\ref{delta2}), obtenemos \begin{equation} \nu=(\frac{2\mu_z}{h})B_o \label{frec} \end{equation} Observamos que la frecuencia es directamente proporcional a la fuerza de campo magnético, lo cual será muy útil para la imagenología.
La torca actuando en el momento magnético es \begin{equation} \boldsymbol{\tau}=\boldsymbol{\mu}\times \boldsymbol{B}_0 \label{torca} \end{equation} La relación de la torca con el momento angular, está dada por \begin{equation} \boldsymbol{\tau}=\frac{d\textbf{J}}{dt} \label{tau-J} \end{equation}
Que podemos relacionar con Eq.(\ref{mommag}) para obtener \begin{equation} \frac{d\boldsymbol{\mu}}{dt}=\gamma(\boldsymbol{\mu}\times\textbf{B}_o) \label{prodcruz} \end{equation} haciendo el producto cruz, obtenemos las 3 relaciones escalares de cada componente
\begin{equation} \frac{d\mu_x}{dt}=\gamma\mu_y B_0 \label{mux} \end{equation} \begin{equation} \frac{d\mu_y}{dt}=-\gamma\mu_x B_0 \label{muy} \end{equation} \begin{equation} \frac{d\mu_z}{dt}=0 \label{muz} \end{equation}
Desacoplando y combinando las dos primeras ecuaciones, obtenemos \begin{equation} \frac{d^2}{dt^2}{\mu_x \choose \mu_y} + (\gamma B_0)^2{\mu_x \choose \mu_y}=0 \label{ecs} \end{equation}
Resolviendo, con las condiciones iniciales: \begin{equation} \boldsymbol{\mu}(0)=\hat{\mathbf{e}}_x\mu_{x0} + \hat{\mathbf{e}}_y\mu_{y0} + \hat{\mathbf{e}}_z\mu_{z0} \label{conini} \end{equation} obtenemos, \begin{equation} \boldsymbol{\mu}(t)= \hat{\mathbf{e}}_x(\mu_{x0}\cos{\omega t} + \mu_{y0}\sin{\omega t}) + \hat{\mathbf{e}}_y(\mu_{y0}\cos{\omega t} - \mu_{x0}\sin{\omega t}) +\hat{\mathbf{e}}_z\mu_{z0} \label{solucion} \end{equation} donde $\omega =\gamma B_0$.
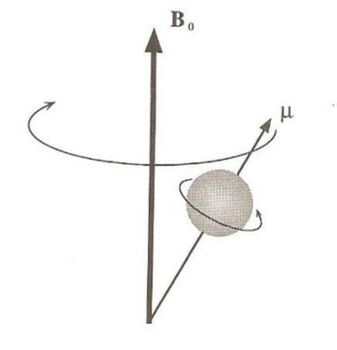
La solución de la Eq.(\ref{solucion}) representa el movimiento de precesión que tiene el momento magnético alrededor del eje del campo $B_0$. La frecuencia de esta precesión es \begin{equation} \nu=\frac{\omega}{2\pi}=\frac{\gamma B_0}{2\pi} \label{larmor} \end{equation} que es llamada frecuencia de Larmor o frecuencia de resonancia del núcleo.
De la frecuencia de Larmor, Eq.(\ref{larmor}) y de la Eq.(\ref{mu-z}), podemos obtener la constante giro-magnética: \begin{equation} \gamma=\frac{4\pi\mu_z}{h} \end{equation} que sustituyendo en Eq.(\ref{larmor}), obtenemos \begin{equation} \nu=\frac{\gamma B_0}{2\pi}=\frac{2\mu_z}{h}B_0 \label{frecuencia} \end{equation} observamos que las Eqs.(\ref{frecuencia}) y (\ref{frec}) son la misma, lo cual nos dice que la frecuencia de la radiación emitida en el cambio del estado "paralelo" al "anti-paralelo" o viceversa, es la frecuencia de Larmor.
Magnetización
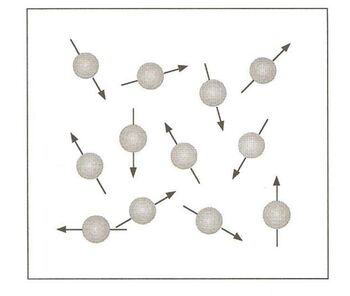
Ahora consideremos un material no magnético; antes de que esté sometido a un campo magnético, todos los núcleos del material, estarán orientados de manera aleatoria, sumando un momento magnético total cero. Una vez que se aplica el campo magnético, cada momento deberá alinearse a favor o en contra del campo magnético.
Sea $N_{\alpha}$ la probabilidad de que un núcleo se encuentre en el estado paralelo, estado de menor energía (estado $\alpha$), y sea $N_{\beta}$ la probabilidad de que se encuentre en el estado anti-paralelo, estado de mayor energía (estado $\beta$), por lo tanto, tendremos que \begin{equation} N_{\alpha} + N_{\beta} = 1 \label{proba} \end{equation} Si el sistema se encuentra en su estado de equilibrio térmico, \begin{equation} \frac{N_{\alpha}}{N_{\beta}} = exp(\frac{\Delta E}{k_B T}) \label{probaBoltz} \end{equation} con $k_B=1.3806\times10^{-23}J\cdot K^{-1}$.
Podemos aproximar Eq.(\ref{probaBoltz}), resultando \begin{equation} \frac{N_{\alpha}}{N_{\beta}} = 1 + \frac{\Delta E}{k_B T} \label{probaBoltzAprox} \end{equation} Tomando $N_{\alpha} \approx N_{\beta} \approx \frac{1}{2}$, obtenemos \begin{equation} N_{\alpha} \approx (1 + \frac{\Delta E}{k_B T})N_{\beta} \approx N_{\beta} + \frac{\Delta E}{k_B T}N_{\beta} \approx N_{\beta} + \frac{\Delta E}{k_B T}(\frac{1}{2}) \end{equation} Entonces \begin{equation} N_{\alpha} - N_{\beta} \approx \frac{\Delta E}{2k_B T} \label{porcentajeProtons} \end{equation} Esta ecuación representa el porcentaje de protones que están alineados con el campo magnético externo.
La magnetización, $\textbf{M}$, se define como el momento magnético neto por unidad de volumen \begin{equation} \textbf{M} = (N_{\alpha} - N_{\beta}) n \mu_z \hat{\mathbf{e}}_z \approx \frac{\Delta E}{2k_B T} n \mu_z \hat{\mathbf{e}}_z \label{magnetizacion} \end{equation} donde $n$ denota el número de protones por unidad de volumen.
$\Delta E$ es proporcional a la fuerza de campo magnético, por lo tanto, $\textbf{M}$ será proporcional a la fuerza de campo magnético. Un campo magnético $B_0$ fuerte es deseable en NMR porque las señales de RF emitidas son obtenidas con la "observación" de la precesión del momento magnético.
Denis (discusión) 05:41 14 jul 2020 (CDT)
Efectos de un pulso de radiofrecuencia
Ahora examinemos los efectos de un campo magnético oscilante de RF , llamaremos a este campo $\textbf{B}_1$, cuya magnitud es $B_{10}$, el cual podemos escribir como \begin{equation} \textbf{B}_1 = \hat{\mathbf{e}}_xB_{10}\cos{\omega t} = \textbf{B}_{CW} + \textbf{B}_{CCW} \label{B1} \end{equation} donde \begin{equation} \textbf{B}_{CW} = \frac{1}{2} B_{10}(\hat{\mathbf{e}}_x\cos{\omega t} - \hat{\mathbf{e}}_y\sin{\omega t}) \label{cw} \end{equation} \begin{equation} \textbf{B}_{CCW} = \frac{1}{2} B_{10}(\hat{\mathbf{e}}_x\cos{\omega t} + \hat{\mathbf{e}}_y\sin{\omega t}) \label{ccw} \end{equation} por lo tanto, el campo magnético $\textbf{B}_1$ se puede escribir como la suma de dos campos rotatorios, uno a favor de las manecillas del reloj $B_{CW}$ y otro en contra de las manecillas del reloj $B_{CCW}$, Eq.(\ref{sumaB1}) \begin{equation} \textbf{B}_1 = \textbf{B}_{CW} + \textbf{B}_{CCW} \label{sumaB1} \end{equation} Si el campo $B_1$ oscila a la misma frecuencia que el sistema en rotación, entonces Eqs.(\ref{cw}) y (\ref{ccw}) se reescriben como \begin{equation} \textbf{B}_{CW} = \frac{1}{2}B_{10}\hat{\mathbf{e}}'_x \label{cw1} \end{equation} \begin{equation} \textbf{B}_{CCW} = \frac{1}{2}B_{10}(\hat{\mathbf{e}}_x'\cos{2\omega_r t} + \hat{\mathbf{e}}_y'\sin{2\omega_rt}) \label{ccw1} \end{equation} Sin embargo, el campo $B_{CCW}$ no tendrá efectos apreciables en el vector de magnetización, por lo tanto, limitaremos el estudio al efecto del campo $B_{CW}$.
Consideremos la Eq.(\ref{prodcruz}), recordando que $\textbf{M}$ obedecerá las mismas ecuaciones que $\boldsymbol{\mu}$, entonces \begin{equation} \frac{d\textbf{M}}{dt}=\gamma(\textbf{M}\times\textbf{B}) \label{prodcruzMagne} \end{equation} pero \begin{equation} \frac{d\textbf{M}}{dt} = \frac{d}{dt}(\hat{\mathbf{e}}_x'M_{x'} + \hat{\mathbf{e}}_y'M_{y'} + \hat{\mathbf{e}}_z'M_{z'} = M_{x'}\frac{d\hat{\mathbf{e}}_x'}{dt} + M_{y'}\frac{d\hat{\mathbf{e}}_y'}{dt} + \hat{\mathbf{e}}_x'\frac{dM_{x'}}{dt} \hat{\mathbf{e}}_y'\frac{dM_{y'}}{dt} \hat{\mathbf{e}}_z'\frac{dM_{z'}}{dt} \label{dM} \end{equation} Ecuaciones de las cuales podemos obtener \begin{equation} \frac{d}{dt}{\hat{\mathbf{e}}_x' \choose \hat{\mathbf{e}}_y'} = \Omega \times \textbf{M} + \frac{\delta\textbf{M}}{\delta t} \label{dxdy} \end{equation} que se puede reescribir como \begin{equation} \frac{d\textbf{M}}{dt} = \Omega \times \frac{\delta \textbf{M}}{\delta t} \label{dMydelta} \end{equation} con $\Omega = -\omega_r\hat{\mathbf{e}}_x$ y $\frac{\delta \textbf{M}}{\delta t}$ representa las derivadas temporales de las componentes de $\textbf{M}$.
Utilizando Eq.(\ref{prodcruzMagne}) y Eq.(\ref{dMydelta}), podemos obtener \begin{equation} \frac{\delta\textbf{M}}{\delta t} = \frac{d\textbf{M}}{dt} - \Omega \times \textbf{M} = \gamma\textbf{M} \times \textbf{B} - \Omega \times \textbf{M} = \gamma \textbf{M} \times (\textbf{M} + \frac{\Omega}{\gamma}) = \gamma\textbf{M} \times \textbf{B}_{eff} \label{parcialM} \end{equation} El valor del campo magnético efectivo, $\textbf{B}_{eff}$ en el marco de referencia en rotación, está dado por \begin{equation} \textbf{B}_{eff} = \hat{\mathbf{e}}_z(B_0 - \frac{\omega_r}{\gamma}) + \hat{\mathbf{e}}_x'\frac{B_{10}}{2} \label{Beff} \end{equation}
Como hemos considerado la frecuencia de rotación igual a la frecuencia de Larmor, la componente $z$ de la expresión anterior se anula. Se ha considerado esa frecuencia porque el tener otras frecuencias causa efectos despreciables; únicamente la frecuenca de Larmor o frecuencias muy cercanas tendrán efectos significativos. \begin{equation} \textbf{B}_{eff} = \hat{\mathbf{e}}_x' \frac{B_{10}}{2} \end{equation} Lo que nos indica que el vector de magnetización tendrá un movimiento de precesión alrededor del campo magnético efectivo.
Aplicando un pulso de RF con duración $T$ segundos, resulta una desviación angular \begin{equation} \theta = \gamma B_{eff}T \label{theta} \end{equation} Los ángulos en los que estaremos interesados son $90 ^{\circ}$ y $180 ^{\circ}$, los cuales se obtienen con pulsos de \begin{equation} T_{90} = \frac{\pi}{2\gamma B_{eff}} \label{90} \end{equation} \begin{equation} T_{180} = \frac{\pi}{\gamma B_{eff}} \label{180} \end{equation}
Ecuaciones de Bloch
Ahora consideremos el fenómeno de NMR a través de las ecuaciones de Bloch. Éstas ecuaciones nos brindan uno de los modelos más simples para el comportamiento de un sistema de spin nuclear después de haber sido excitado con pulsos, pero tiene una limitación, que está basado en principios clásicos, por lo que no puede explicar los detalles más finos del espectro de NMR.
Las ecuaciones de Block pueden ser escritas como \begin{equation} \frac{dM_x}{dt} = \gamma(\textbf{M} \times \textbf{B})_x - \frac{M_x}{T_2} \label{BlochTrans} \end{equation} \begin{equation} \frac{dM_y}{dt} = \gamma(\textbf{M} \times \textbf{B})_y - \frac{M_y}{T_2} \label{Blochy} \end{equation} \begin{equation} \frac{dM_z}{dt} = \gamma(\textbf{M} \times \textbf{B})_z + \frac{M_0 - M_z}{T_1} \label{Blochz} \end{equation} donde $T_1$ y $T_2$ son el tiempo de relajación longitudinal y transversal, respectivamente, y $M_0$ denota el valor de la magnetización en el equilibrio, el cual se asume en la dirección $z$. El efecto del proceso de relajación es el regreso del vector de magnetización a su posición de equilibrio.
Estamos interesados en analizar el caso en el cual el vector de magnetización ha sido desviado por un pulso de $90 ^{\circ}$; y consideramos que el campo de RF ha sido aplicado en el plano transverso, con lo que inicialmente tenemos \begin{equation} \textbf{M}_0 = \hat{\mathbf{e}}_x M_0 \label{BlochMini} \end{equation} Observamos que las Eqs.(\ref{BlochTrans}) y (\ref{Blochz}) son muy similares a las ecuaciones que describen el comportamiento de un momento magnético aislado.
Podemos reescribir las Eqs.(\ref{BlochTrans}) y (\ref{Blochz}) como \begin{equation} \frac{dM_x}{dt} = \gamma M_y B_0 - \frac{M_x}{T_2} \label{BlochMx} \end{equation} \begin{equation} \frac{dM_y}{dt} = -\gamma M_x B_0 - \frac{M_y}{T_2} \label{BlochMy} \end{equation} \begin{equation} \frac{dM_z}{dt} = \frac{M_0 - M_z}{T_1} \label{BlochMz} \end{equation}
En donde hemos considerado que debido a que $\textbf{B}$ se encuentra únicamente en la dirección $z$, la cantidad $\textbf{M} \times \textbf{B}$ nunca tendrá una componente en la dirección $z$ diferente de cero, por lo tanto, la Eq.(\ref{Blochz}) queda reescrita como Eq.(\ref{BlochMz}).
Las soluciones de las Eqs.(\ref{BlochMx}), (\ref{BlochMy}) y (\ref{Blochz}) son \begin{equation} M_x(t) = M_0 \exp(-\frac{t}{T_2}\cos(\gamma B_0 t)) \label{BlochMxSol} \end{equation} \begin{equation} M_y(t) =-M_0 \exp(-\frac{t}{T_2}\sin(\gamma B_0 t)) \label{BlochMySol} \end{equation} \begin{equation} M_z(t) = M_0(1 - \exp(-\frac{t}{T_1})) \label{BlochMzSol} \end{equation} En la última de éstas ecuaciones, se ha impuesto el valor inicial \begin{equation} M_z(0) = 0 \label{BlochMzIni} \end{equation} De las Eqs.(\ref{BlochMxSol}), (\ref{BlochMySol}) y (\ref{BlochMzSol}), podemos observar el regreso del vector de magnetización a su estado de equilibrio.
Hardware de la imagen por resonancia magnética nuclear
La parte tangible de la Resonancia Magnética Nuclear; entre las partes importantes, se encuentran:
El imán principal
En todos los experimentos de NMR es necesario generar un campo magnético fuerte (el campo $B_0$), el cual debe ser uniforme en el volumen de interés. El imán principal es usado para generar un campo primario, mientras que las bobinas gradiente crean un gradiente que estará superpuesto sobre el campo principal.
Los sistemas espectroscópicos están disponibles con magnitud de los campos tan altos como $17.5$ $T$. Los sistemas de imagenología clínica normalmente tienen campos no mayores a $2$ $T$, cuyo principal requerimento es que su campo sea uniforme.
El imán principal rara vez produce un campo con suficiente uniformidad por sí mismo, por eso las bobinas "shim" son usualmente empleadas. Las bobinas shim son un grupo de bobinas diseñadas para producir un campo polarizado en la misma dirección que el campo principal.
Si la uniformidad del campo de el imán principal es conocida, las bobias shim pueden ser agrupadas para crear gradientes que cancelen (por superposición) las componentes inhomogeneas del campo principal.
Depende de la aplicación en la que se empleen, pueden ser utilizados imanes permanentes, resistivos o superconductores.
Antenas de RF
En NMR, es necesario irradiar la muestra a estudiar con un campo de RF, el campo $B_1$, con el fin de inclinar la magnetización lejos de su estado de equilibrio y generar una señal NMR detectable. Para llevarlo a cabo, se debe excitar el núcleo en precesiones coherentes, esto requiere el acoplamiento entre el núcleo y alguna fuente de poder de RF (el transmisor); para recibir una señal significativa, uno necesita un dispositivo para acoplar el núcleo a algún circuito externo; éstos dispositivos son llamados bobinas de RF, también llamados resonador de RF u onda de RF. Éstos dispositivos son responsables de frecuencias en la banda definida por la frecuencia de Larmor.
Es importante que estas bobinas generen un campo magnético uniforme; las inhomogeneidades del campo introducirán distorciones en la imagen obtenida
Las antenas de RF pueden ser transmisoras, receptras o puede cumplir con las dos funcionalidades:
$\textbf{La antena transmisora}$ es la responsable de la forma del pulso, duración, poder y sincronización (velocidad de repetición).
Para generar un pulso de RF, primero, el transmisor utiliza un sintetizador de frecuencia para generar una oscilación de frecuencia definida por el usuario. Posteriormente, un generador de formas de ondas crea una forma del pulso, creada por el usuario, la cual será multiplicada con el tono puro, entonces se crea un pulso de RF. Transmisores modernos generalmente utilizan generadores de formas del pulsos digitales, por lo tanto el tiempo mínimo de exposición debe ser una consideración importante.
$\textbf{La antena receptora}$ convierte la señal recibida del transmisor de RF en una forma adecuada, se utiliza un convertidor analógico a digital (ADC) o un digitalizador; algún circuito deberá ser utilizado.
La primera etapa del receptor es algunas veces llamada "amplificador de alto ruido (LNA)" el cual previene la señal débil recibida, pues es denominada ruido. La segunda etapa del receptor es una línea de transmisión para llevar la señal de RF a la bobina de RF, a una localización donde es más conveniente tener circuitos voluminosos.
Aportacion de: Denis (discusión) 14:58 14 jul 2020 (CDT)