El arco iris
El arcoiris
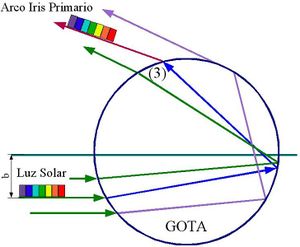
El ARCO IRIS es la exhibición mas espectacular del espectro de la luz blanca en la naturaleza. Las condiciones requeridas para la aparición de este fenómeno, son que el Sol esté brillando en alguna parte del cielo y la lluvia esté cayendo en la parte opuesta. Dando uno la espalda al Sol, se pueden ver arcos de círculos, el arco iris primario brillante, y, a veces, el arco iris secundario, más débil, con los colores invertidos. Vistos desde alguna altura conveniente o desde un avión, estos arcos pueden formar círculos completos, cuyo centro común esta situado es la dirección de la sombra del observador.
La teoría elemental del arco iris fue dada primero por Antonius de Demini en el año de 1611 y, posteriormente, desarrollado con mayor exactitud por Descartes. Las características generales de los arcos primario y secundario son explicadas satisfactoriamente al considerar solo la reflexión y la refracción de la luz por una gota esférica de lluvia. Para comprender como se produce el fenómeno, concentremos primero nuestra atención en una sola gota de lluvia. Se muestra un rayo de luz solar entrando entrando en una gota de lluvia por un punto A, cerca de su parte superior. En este punto, algo de luz se refleja, y el resto se refracta dentro de la esfera liquida. En esta primera refracción la luz se dispersa en sus colores espectrales, el color violeta es el que se desvía más, y el rojo el que se desvía menos. Llegando al lado opuesto de la gota, cada color es parcialmente refractado hacia afuera (dentro del aire), y en parte reflejado hacia atrás (dentro del liquido). Alcanzando la superficie en el límite inferior, cada uno de los colores es otra vez reflejado y refractado. Esta segunda refracción es muy similar a la de un prisma, en donde la refracción en la segunda superficie aumenta la dispersión ya producida en la primera. Ésta es la trayectoria de la luz en las miles de gotas que producen el brillante arco iris.
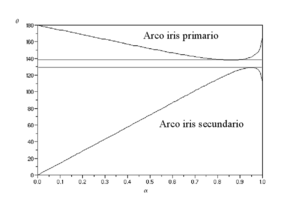
Demostrar que el ángulo del arco iris primario pasa por un ángulo de aproximadamente 138º.
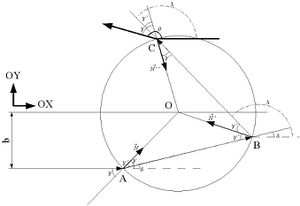
Sea la circunferencia la proyección en dos dimensiones de una esfera de radio r centrada en O.
La dirección del rayo es representada por la recta . Sin embargo, como b es un parámetro que tomará los valores entre 0 y r, expresaré la recta como , siendo un número entre 0 y 1.
La descripción algebraica de la circunferencia es .
De ambas se deduce que el punto de incidencia del rayo con la circunferencia es .
La recta que pasa por y sería::
El vector normal interior a la superficie es::
Haciendo el producto vectorial de un vector unitario en la dirección del eje OX, , y el vector normal obtengo::
luego de aquí se deduce que::
Si aplico la ley de Snell::
Siendo y .
El ángulo que forma respecto de la horizontal es::
Según observamos en la figura, el triángulo es isósceles de lado r, luego el ángulo de reflexión en es::
El ángulo .
Igualmente en el triángulo OBC, el ángulo del vértice C es . El ángulo de refracción, por la ley de Snell, vuelve a ser . El ángulo total desviado respecto a la horizontal, puedo calcularlo como::
que puede expresarse como:: .
es una función de . Puede expresarse como::
Haciendo la derivada::
Igual a cero, para calcular el mínimo, y éste se produce para . Corresponde a un ángulo::
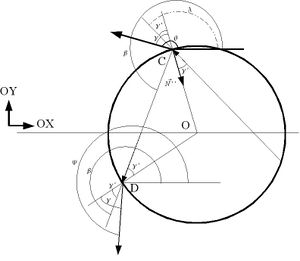
Demostrar que el ángulo del arco iris secundario pasa por un ángulo de aproximadamente 130º.
Nos basamos en la demostración anterior. Se produce una reflexión más. Nuestro objetivo es calcular el ángulo de salida en función de .
El ángulo puede expresarse como (punto C)::
De igual forma, el ángulo de salida respecto de la horizontal es::
es una función de . Puede expresarse como::
Haciendo la derivada::
Igual a cero, para calcular el máximo, y éste se produce para . Corresponde a un ángulo::
¿Nos hemos equivocado? Bueno, algo sí. Hemos supuesto que la dirección de impacto es la recta . Si supongo que b<0, entonces es un número entre -1 y 0. Si supongo que el impacto es por encima de la horizontal, en vez de tomar lo tomo como y el ángulo sería:: .
Arcos supernumerarios. Teoría de Thomas Young.
Aparecen en el lado interno del arco primario, en la zona iluminada. En esta zona, hay rayos de clase (3), que tras haber sido difundidos salen con el mismo ángulo, a uno y otro lado del ángulo mínimo del arco iris. Estos rayos han recorrido diferentes caminos en la gota y salen en puntos distintos.
En la época de Descartes o Newton se ignoraba el caracter ondulatorio de la luz, luego no se pudo prever esta interferencia entre estos dos rayos. El primero que dió una explicación coherente fue Young.
Dependiendo de los caminos ópticos que recorre uno más que el otro se presentan franjas brillantes u oscuras (interfieren constructivamente si difieren en valores enteros de longitud de onda).
El camino que recorre el rayo dentro de la gota sí depende del radio (no como antes para los rayos principales), luego su aparición depende del radio de las gotas. Para gotas grandes, los caminos de los rayos difieren más que para gotas pequeñas, y es más difícil que coincidan en longitudes de onda enteras. Para gotas pequeñas los caminos ópticos son prácticamente iguales y es más fácil que interfieran constructivamente. Para radios superiores a 1mm es casi imposible distinguirlos.
La superposición de colores tiende a eliminar también los arcos. Además, como las gotas se hacen más grandes a medida que caen, se explica que se formen inmediatamente debajo del primer arco.
También encontramos una explicación más razonable sobre la banda oscura de Alejandro. La débil luminosidad de la banda no sólo se explica con intensidad residual de arcos iris de clase superior a (4) sino también por fenómenos de difracción.
Así que debemos utilizar, en la explicación de la formación del arco iris, dos teorías de interacción: la de la luz consigo misma (interferencia) y la de la luz con obstáculos (difracción).
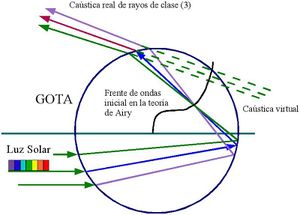
Teoría de Airy. Teoría del momento cinético.
En 1835, Richard Potter explicó que el cruce de varios rayos daba lugar a una caústica. Una cáustica es la envolvente de un sistema de rayos y se asocia a altos valores de intensidad. La intensidad aumenta hasta llegar a la cáustica y luego disminuye rápidamente.
Potter mostró que el rayo de clase 3 de Descartes (desviación mínima) se podría tratar como una cáustica. Todo rayo que salga por el lado iluminado se acerca a este rayo en el infinito (no los hay en el lado no iluminado). El problema de hallar la intensidad del arco y su distribución se reduce a determinar la distribución de la misma en la proximidad de la cáustica.
Airy fué el primero en intentar demostrar tal distribución. Su razonamiento le hizo usar las teorías de la propagación de la luz de Huygens (mejoradas por Fresnel). Estas decían que cada punto de un frente de ondas se podría reconstruir a partir de estas ondas elementales secundarias como su envolvente.
Según el teorema de Kirchoff, conociendo la distribución de amplitudes de las ondas secundarias de un frente de ondas, puedo saber cuánto vale ésta en otro punto cualesquiera. Podría pues reconstruir los frentes de onda y dar amplitudes en cada punto si conociera un frente de ondas y su valor de amplitudes para una gota. Como esto es imposible de saber, Airy probó con un frente de ondas inicial escogido según las consideraciones siguientes:
1º) Es normal el frente a todos los rayos de clase (3). 2º) Tiene un punto de inflexión en el rayo de Descartes (rayo de desviación mínima). 3º) Los valores (amplitudes) se escogieron siguiendo hipótesis normales en la teoría de la difracción.
la distribución de intensidades, tras laborioso cálculo, sale en función de una integral (función de Airy). Esta distribución es análoga a la distribución de intensidades de difracción que aparece en la sombra de un filo rectilíneo para la zona oscura o banda de Alejandro. esta disminuye al alejarnos del ángulo de desviación mínima.
La función de Airy es:: siendo la intensidad de luz transmitida en una situación de interferencia de haces múltiples.
F es la finura: , siendo el coeficiente de reflexión normal aire-agua.
es el desfase que se produce en una lámina plano paralela::
es el ángulo refractado::
La finura F es aproximadamente 0.085.
Aportación de: Antonio de Jesus Jimenez Lopez 06:00 17 abr 2012 (UTC) Aportación de: Carlosmiranda (discusión) 17:33 22 nov 2020 (CST)