Dielectricos
Dieléctricos
Un material dieléctrico es una sustancia que es un mal conductor de la electricidad, pero un defensor eficaz de campo electrostáticos.Si el flujo de corriente entre los polos opuestos de carga eléctrica se mantiene a un minuto mientras que las líneas de flujo de electrostática no se impide o se interrumpe, un campo electrostático puede almacenar la energía.Esta propiedad es útil en el condensador, especialmente en las frecuencias de radio.Los materiales dieléctricos son utilizados en la construcción de líneas de transmisión de radiofrecuencia.Faraday descubrió que cuando el espacio entre los dos conductores de un condensador se ve ocupado por un dieléctrico, la capacidad aumenta en un factor que es característico del dieléctrico y que se denomina constante dieléctrica.
Un dieléctrico debilita el campo eléctrico entre las placas de un condensador pues, en presencia de un campo eléctrico extremo, las moléculas del dieléctrico producen un campo eléctrico extremo, las moléculas del dieléctrico producen un campo eléctrico adicional de sentido opuesto al del campo externo.
Si el campo eléctrico original entre las placas de un condensador sin dieléctrico es $Eo$, el campo en el dieléctrico es:
Donde K es la cte. dieléctrica. El cálculo detallado de la interacción dipolo-dipolo es muy difícil habida cuenta de la complicada estructura de líquidos y sólidos. En una aproximación para dieléctricos no polares debida a Lorentz, esta interacción se calcula separando el dieléctrico en dos partes mediante una esfera imaginaria de radio r, centrada en la molécula que ocupa el lugar donde se pretende calcular el campo local. El radio de la esfera se elige de manera que contenga a las moléculas más próximas, de forma que el campo creado por ellas ha de ser tenido en cuenta de forma individualizada.Fuera de la esfera y, por tanto, a distancia relativamente grandes, el dieléctrico puede considerarse como un medio continuo de constante dieléctrica y polarización .
El campo eléctrico,. que actúa sobre una molécula situada en el centro de la esfera, O (fig. 4.1), viene dado por la suma de las siguientes contribuciones:
1) Campo en el interior del dieléctrico, E(campo medio macroscópico).
2) Campo . debido a la carga superficial de polarización sobre la esfera imaginaria, . (contribución externa a la esfera)
3) Campo debido a los dipolos inducidos situados en el interior de la esfera,.
Cuando un material con propiedades conductoras está sometido a un campo eléctrico . La densidad de la corriente, . a través del conductor se puede escribir en primera aproximación como:: Donde . representa la conductividad del material. En los dieléctricos, sin embargo, cuando los campos eléctricos aplicados son variables con el tiempo aparece una nueva contribución a la densidad de corriente, que , de acuerdo con las ecuaciones de Maxwell, viene dada por:
siendo . La llamada corriente de desplazamiento, y D el vector desplazamiento eléctrico. Cuando están presentes ambos tipos de corrientes, la de conducción y la de desplazamiento, la densidad de corriente total, ., será::
Podemos expresar el valor de . en función del vector de polarización P, mediante la relación: .
Con objeto de estudiar de forma completamente general la respuesta de un dieléctrico, ante un campo eléctrico , variable con el tiempo, conviene precisar la naturaleza de la función D(t) correspondiente a dicho campo, definida a través de la relación:
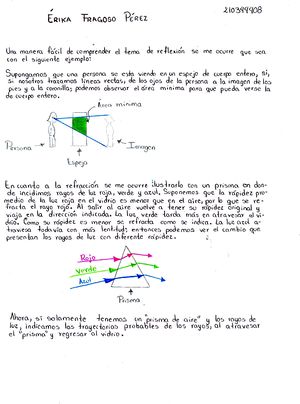
Donde es la constante dieléctrica del material en cada instante t. Trataremos primero el caso más simple, consiste en la aplicación sobre el dieléctrico de un pulso eléctrico rectangular, definido por:: Para un tiempo comprendido entre un tiempo t comprendido entre un tiempo y + , y por para el resto. Matemáticamente esta función se puede descomponer en una suma de dos funciones escalón, T(t), de la forma: .
TIPOS DE DIELÉCTRICO.
En los materiales dieléctricos o aislantes no existen electrones libres que se puedan desplazar por ellos; todos se encuentran ligados a sus átomos. Por eso, cuando se aplica un campo externo a un dieléctrico su comportamiento es muy distinto al de los conductores. Las moléculas de los dieléctricos pueden ser de dos tipos: polares o no polares. Los dieléctricos con moléculas polares son los que presentan desigualdad de cargas eléctricas dentro de las mismas moléculas, es decir tiene un polo positivo y un polo negativo. Los dieléctricos con moléculas no polares son los que tiene centradas las cargas positivas y negativas, es decir no hay distinción entre las cargas de superficie.
Ejemplos de dieléctricos:
- Polares:el agua y el nailon
- No polares: el aire y el hidrógeno
PROCESOS DE POLARIZACIÓN
En el momento en que a un material dieléctrico se le aplica un campo eléctrico, se verifica una alineación parcial de los dipolos con el campo eléctrico, generando así densidades de carga en las superficies del dieléctrico (cercanas a las placas del capacitor). La alineación es proporcional al campo eléctrico, dando así cabida a un nuevo valor de campo eléctrico, el cual será $E=(E_i-E)$ inducido, debido a que al polarizar al dieléctrico se genera un nuevo campo eléctrico generado por las cargas inducidas de las superficies de este.
APLICACIONES
Los dieléctricos se utilizan en la fabricación de condensadores, para que las cargas reaccionen. Cada material dieléctrico posee una constante dieléctrica. Tenemos para los siguiente dieléctricos: vacío tiene ; aire (seca) tiene ; teflón tiene ; nylon tiene ; papel tiene ; agua (Químicamente pura) tiene .
Los dieléctricos más utilizados son el aire, el papel y la goma. La introducción de un dieléctrico en un condensador aislado de una batería, tiene las siguientes consecuencias:
- Disminuye el campo eléctrico entre las placas del condensador.
- Disminuye la diferencia de potencial entre las placas del condensador, en una relación .
- Aumenta la diferencia de potencial máxima que el condensador es capaz de resistir sin que salte una chispa entre las placas (ruptura dieléctrica).
- Aumento por tanto de la capacidad eléctrica del condensador en veces.
- La carga no se ve afectada, ya que permanece la misma que ha sido cargada cuando el condensador estuvo sometido a un voltaje.
Normalmente un dieléctrico se vuelve conductor cuando se sobrepasa el campo de ruptura del dieléctrico. Esta tensión máxima se denomina rigidez dieléctrica. Es decir, si aumentamos mucho el campo eléctrico que pasa por el dieléctrico convertiremos dicho material en un conductor.
Aportación de: Carlosmiranda (discusión) 16:55 22 nov 2020 (CST)


























![E(t)\ =E_o[T(t-\theta\,)-T(t-\theta\,-d\theta\,)]](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/2b2863410cf83affebedded53089308812ba0838)







