Analogia electrica de vibraciones mecanicas
Introducción
En el trabajo de crear modelos matemáticos que describan los fenómenos naturales, se han dado cuenta que algunos de ellos pueden ser descritos con expresiones matemáticas muy similares entre si. Desde la relación gravitacional de Newton y la relación de Coulomb, hasta las vibraciones de un péndulo y un circuito con corriente alterna. Los últimos dos fenómenos mencionados tienen en común su comportamiento, ambos pueden ser descritos como vibraciones libres y pueden ser descritos por la ecuación del oscilador armónico simple.
Para poder relacionar un fenómeno con el oscilador armónico, basta con describir al fenómeno con una expresión matemática que se parezca a la siguiente
\begin{equation} \ddot{\psi}+\omega^{2}\psi=0. \label{oa} \end{equation}
La solución de (\ref{oa}) está en plano de los números complejos
\begin{eqnarray*} \psi=A e^{i \omega t}= A(\cos (\omega t) + i\mathrm{sen} (\omega t)). \end{eqnarray*}
En éste texto se utilizará sólo la parte real,
\begin{eqnarray*} \psi= A \cos (\omega t). \label{sol} \end{eqnarray*}
Dicha solución propuesta satisface sin problemas a (\ref{oa}) y describe un fenómeno de vibración.
El estudio de (\ref{oa}) ha ayudado al estudio de varios fenómenos, la única diferencia es la interpretación de los resultados y el análisis de las gráficas. Los comportamientos pueden ser los mismos, pero los fenómenos no.
Aportación de usuario: Juan Daniel Rivera Bautista (discusión) 21:46 12 jul 2020 (CDT)
Circuitos LC
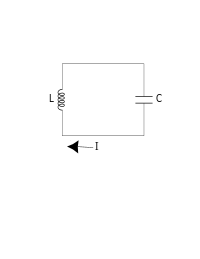
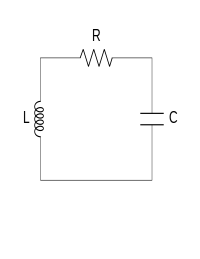
Se habla de un circuito $LC$ cuando se tiene sólo capacitores e inductores. En éste texto, se analizará un circuito en serie donde se tendrá sólo un capacitor y también sólo un inductor. También, parte del objetivo de éste texto es realizar un análisis comparativo con el oscilador armónico.
El circuito está ilustrado en la figura anterior, es de una sola malla y, como ya se mencionó, sólo tiene un capacitor y un inductor, no se tiene una fuente de voltaje externo. Al ser una sola malla y estar en serie, la expresión matemática que describe al circuito es
\begin{equation} L\frac{dI}{dt}=-\frac{\int Idt}{C}. \label{cir} \end{equation}
Donde $L$ es la inductancia y $C$ es la capacitancia. La carga queda descrita por $-\int Idt$, eso significa que la carga dependerá del tiempo. En éste circuito el potencial queda descrito por $\frac{\int Idt}{C}$.
Lo siguiente es pasar la expresión (\ref{cir}) a una que se parezca al oscilador armónico. Primero, la carga quedará descrita por una función dependiente del tiempo y será $-\psi(t)$. Eso hace que la corriente $I$ sea $\dot{\psi}$ y la derivada de la corriente es $\ddot{\psi}$, por lo tanto, nuestra expresión se puede reescribir de la siguiente forma
\begin{equation} \ddot{\psi}+\omega^{2} \psi=0. \label{cir2} \end{equation}
En la expresión (\ref{cir2}) sólo se dividió todo entre $L$ y se usó la siguiente igualdad $\omega^{2}=\frac{1}{LC}$. Después de esto, ya se tiene la ecuación del movimiento armónico y la solución que se propone es
\begin{eqnarray*} \psi=A\cos(\omega t+\phi_{0}) \end{eqnarray*}
Donde $\phi_{0}=0$, así, al derivar y evaluar con las condiciones ideales, se puede obtener la corriente máxima, se hace esto porque es un cálculo muy común cuando se resuelven circuitos.
\begin{eqnarray*} \dot{\psi}=-A \omega \mathrm{sen}(\omega t) \end{eqnarray*}
Si se evalúa en $t=\frac{\pi}{2\omega}$ la función seno vale 1 y se obtiene el máximo de la corriente, eso da como resultado que $A\omega=I_{m}$, donde $I_{m}$ es la amplitud máxima de la corriente o la corriente máxima. Pero hay que recordar que la carga es $-\psi$, eso hace que la corriente sea $-\dot{\psi}$
\begin{equation} I(t)=I_{m}\mathrm{sen}(\omega t) \label{corriente} \end{equation}
Una vez hecho esto, la carga se puede reescribir con la constante $I_{m}$
\begin{equation} q(t)=-\frac{I_{m}}{\omega}\cos(\omega t+\phi_{0}), \label{carga} \end{equation}
y también se puede escribir el Voltaje
\begin{equation} V(t)=-\frac{I_{m}}{\omega C}\cos(\omega t+\phi_{0}). \label{voltaje} \end{equation}
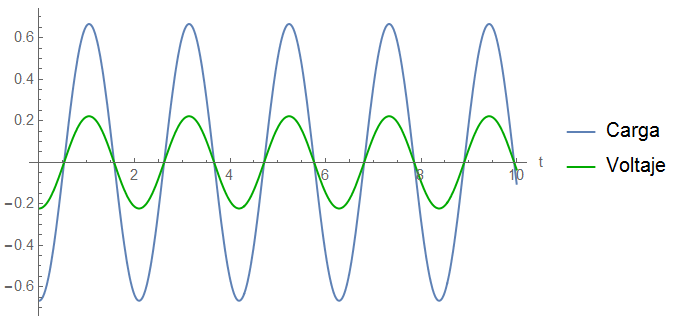
Al observar las funciones (\ref{carga}) y (\ref{voltaje}), se puede notar que son proporcionales, la única diferencia es la capacitancia, la cual hace que la amplitud del Voltaje sea menor a la amplitud de la Carga pero, el comportamiento es el mismo, alcanza sus valores máximos al mismo tiempo y también son cero al mismo tiempo. En la siguiente figura se puede apreciar de mejor manera el comportamiento descrito
A la figura no se le pone unidades en el eje Y porque las unidades son distintas para las curvas, pero se grafican juntas para poder apreciar que tienen el mismo comportamiento, se comportan como una vibración.
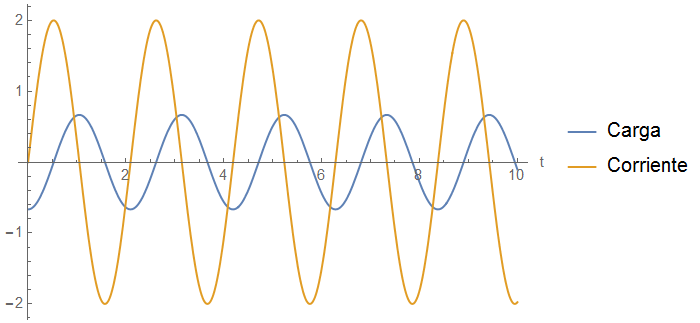
La Corriente, a diferencia de la Carga y del Voltaje, tiene el mismo comportamiento pero a distintos tiempos. Cuando la Carga está en su valor máximo, la Corriente es cero, pero cuando la corriente está en su valor máximo, la carga es cero, a éste tipo de corriente se le llama Corriente alterna. Éste comportamiento queda ilustrado en la siguiente figura
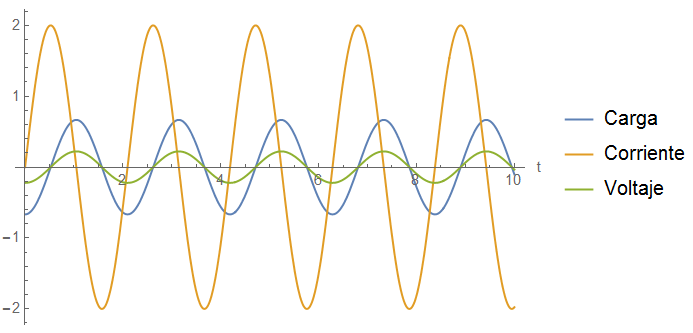
Hay que resaltar que los comportamientos son igualas a una vibración, pero los fenómenos son causados por capacitores, inductores y corrientes eléctricas. La última figura contiene las tres curvas para poder observar los tres cambios el mismo tiempo.
Energía
Para hacer la analogía de la energía, se tiene que partir de un paso más atrás de la ecuación (\ref{oa}), mostrando su forma antes de juntar las constantes que forman a $\omega$, esa expresión matemática es la siguiente
\begin{equation} m\ddot{\psi}=-\kappa \psi. \label{masa} \end{equation}
Donde $m$ es la masa y $\kappa$ es la constante restaurativa, hay que recordar que éste modelo parte de un resorte con una masa en un extremo.
Si (\ref{masa}) se compara con (\ref{cir}), se pueden asociar las constantes. Se puede decir que $L$ es $m$ y que $\frac{1}{C}$ es $\kappa$. Éstas semejanzas hacen que se puedan asociar otras cantidades físicas como la energía cinética y la energía potencial.
La energía cinética queda descrita por
\begin{eqnarray*} \mathcal{E}_{k}=\frac{1}{2}m\dot{\psi}^{2}. \end{eqnarray*}
Si se usan las equivalencias, se obtiene la siguiente expresión
\begin{equation}
U_{B}=\frac{1}{2}LI^{2}.
\label{l}
\end{equation}
Donde (\ref{l}) es la expresión de la energía almacenada por un campo magnético.
La energía potencial en el oscilador es
\begin{eqnarray*} \mathcal{E}_{p}=\frac{1}{2}\kappa\psi^{2}. \end{eqnarray*}
Al igual que con la energía cinética, aquí también existe una equivalente
\begin{equation} U_{E}=\frac{1}{2}\frac{1}{C}q^{2}. \label{c} \end{equation}
Donde (\ref{c}) describe la energía almacenada en un campo eléctrico.
Por último, la energía total sería la suma de ambas
\begin{equation} \mathcal{E}=U_{E}+U_{B}. \label{eb} \end{equation}
Como conclusión, se puede decir que se confirmó que un circuito $LC$ se puede comportar como una vibración y se puede describir con la ecuación del oscilador armónico. Lo único que cambia son las interpretaciones de los resultados.
Circuito RCL
Como lo dice el nombre, el circuito $RCL$ está conformado por resistencias, capacitores e inductores. En ésta ocasión también se resolverá el ejemplo más simple que trata de un circuito en serie donde se tiene sólo una resistencia, un capacitor y un inductor.
A la ecuación (\ref{cir}), sólo se le agrega la parte de la resistencia, lo que hace que quede como
\begin{equation} L\frac{dI}{dt}+\frac{\int Idt}{C}=-RI. \label{res} \end{equation}
Siguiendo con el cambio de la notación como se hizo en la sección anterior, la ecuación queda de la siguiente forma
\begin{equation} \ddot{\psi}+\gamma\dot{\psi}+ \omega^{2} \psi=0. \label{resvib} \end{equation}
Donde $\gamma=\frac{R}{L}$. Después de hacer los cambios en la notación, es evidente que la ecuación (\ref{resvib}) es la ecuación del oscilador armónico amortiguado. Algo que se debe resaltar es que, en el oscilador armónico, se sabe que $\gamma=\frac{b}{m}$, donde $b$ es la resistencia, es una casualidad que se llamen igual $b$ y $R$, ya que tienen el mismo comportamiento pero en fenómenos diferentes, ambas constantes son parte de una fuerza de oposición.
Para (\ref{resvib}) se propone como solución la siguiente función
\begin{eqnarray*} \psi=C e^{\alpha t}. \end{eqnarray*}
Lo que da como resultado la siguiente ecuación
\begin{eqnarray*} \alpha^{2}+\gamma \alpha + \omega^{2} =0. \end{eqnarray*}
Al ser una ecuación cuadrática, da como resultado
\begin{eqnarray*} \alpha=-\frac{1}{2}\gamma\pm \sqrt{\frac{1}{4}\gamma^{2}-\omega^{2}}. \end{eqnarray*}
Ahora, manipulando solamente la parte de la raíz cuadrada, se tomará en cuenta que el discriminante es negativo y factorizamos $\omega^{2}$,
\begin{eqnarray*} \omega\sqrt{-\left(1-\frac{1}{4}\frac{\gamma^{2}}{\omega^{2}}\right)}=i\omega\sqrt{\left(1-\frac{1}{4}\frac{\gamma^{2}}{\omega^{2}}\right)}. \end{eqnarray*}
La solución queda de la forma siguiente
\begin{eqnarray*} \psi=A \mathrm{exp} \left[-\frac{1}{2}\gamma \pm i\omega\sqrt{\left(1-\frac{1}{4}\frac{\gamma^{2}}{\omega^{2}}\right)}\:t\right]. \end{eqnarray*}
Pero sólo se usará la parte real, enconces la solución se queda de la siguiente forma
\begin{equation} \psi=A \mathrm{exp}\left[ -\frac{1}{2}\gamma \right] \cos \left( \omega\sqrt{\left(1-\frac{1}{4}\frac{\gamma^{2}}{\omega^{2}}\right)}\:t\right). \label{amor} \end{equation}
Donde $t$ va afuera de la raíz.
Como se puede ver, la función (\ref{amor}) es la solución para el oscilador armónico amortiguado,dependiendo de los valores de las constantes $\gamma$ y $\omega$ se tendrán diferentes tipos de amortiguamiento.
Lo siguiente es escribir las cantidades que son de interés cuando se resuelven circuitos.
La carga es $-\psi$,
\begin{equation} q(t)=-A \mathrm{exp}\left[ -\frac{1}{2}\gamma \right] \cos \left( \omega\sqrt{\left(1-\frac{1}{4}\frac{\gamma^{2}}{\omega^{2}}\right)}\: t\right). \label{qr} \end{equation}
El valor de la constante $A$ sale de la carga inicial que tiene el capacitor.
El Voltaje lo sigue poniendo la parte del capacitor,
\begin{equation} V(t)=-\frac{A}{C} \mathrm{exp}\left[ -\frac{1}{2}\gamma \right] \cos \left( \omega\sqrt{\left(1-\frac{1}{4}\frac{\gamma^{2}}{\omega^{2}}\right)}\: t\right). \end{equation}
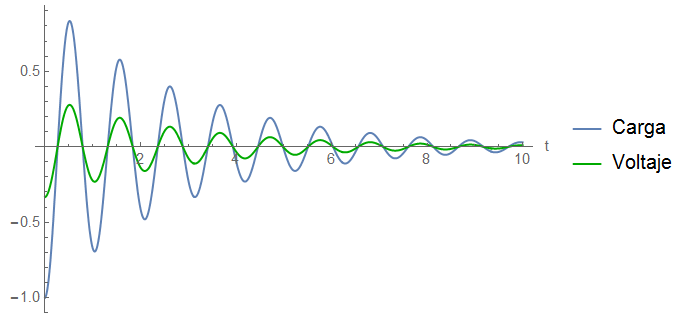
Éstas condiciones hacen que sus comportamiento sea el mismo, alcanzarán sus valores máximos y mínimos ( son máximos y mínimos locales) y serán cero al mismo tiempo, lo único que cambia es la amplitud. Se puede observar que ambas tendrán el comportamiento de una función coseno, pero decrecerá con el paso del tiempo, esto se debe a la resistencia. La resistencia queda como una fuerza de oposición y además hace que pierda energía el sistema. En la analogía con el oscilador armónico amortiguado, la resistencia se podría ver como una fuerza de fricción, lo que también hace que pierda energía el sistema.
A continuación se muestran las gráficas de un amortiguamiento suave, eso se da cuando $\omega^{2}>\frac{1}{4}\gamma^{2}$, pero la diferencia no es muy grande. Hay que resaltar que $\omega$ contiene la información del capacitor y $\gamma$ contiene la información de la resistencia.
La corriente es $-\dot{\psi}$,
\begin{equation} I(t)=A \mathrm{exp}\left[ -\frac{1}{2}\gamma \right] \left( \frac{1}{2}\gamma\cos \left( \omega_{f}t\right)+ \omega_{f} \mathrm{sen} \left( \omega_{f}t\right)\right). \label{ir} \end{equation}
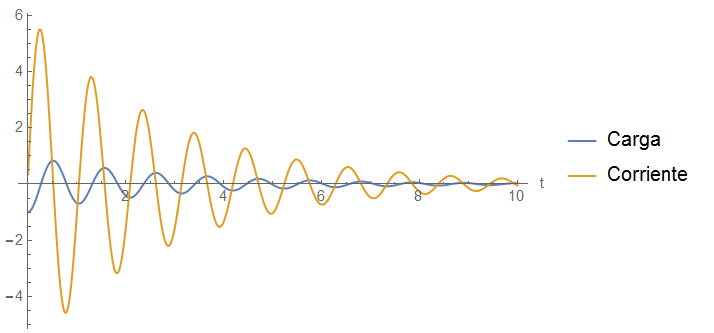
Donde $\omega_{f}= \omega\sqrt{\left(1-\frac{1}{4}\frac{\gamma^{2}}{\omega^{2}}\right)}$. La corriente sigue teniendo casi las mismas cualidades que en un circuito $LC$, vale cero cuando la carga está en su máximo y mínimo locales local y sus valores máximos y mínimos locales se dan cuando la carga es cero, el único comportamiento distinto es que también decrece de forma exponencial ya que también se ve afectada por la Resistencia.
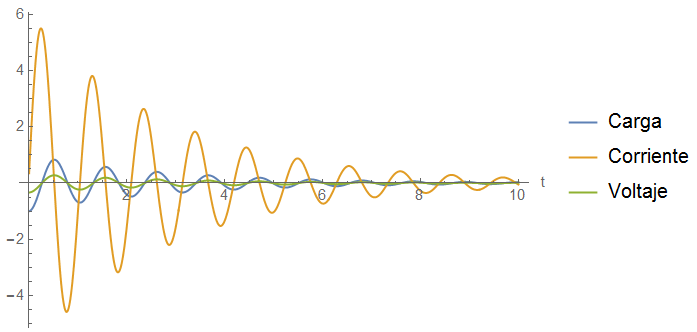
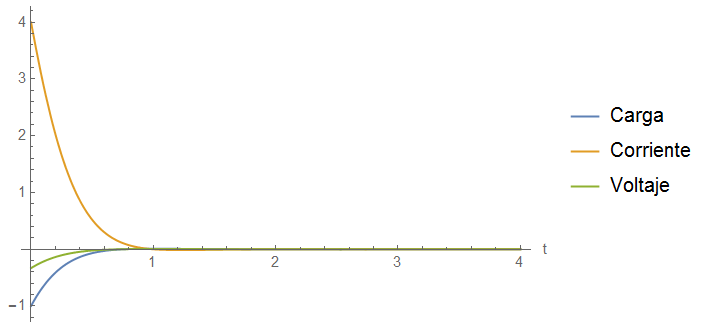
En la siguiente figura, se grafican las 3 curvas juntas para poder comparar mejor sus comportamientos. Hay que el comportamiento de una vibración amortiguada, resultado de resolver la ecuación del oscilador armónico amortiguado.
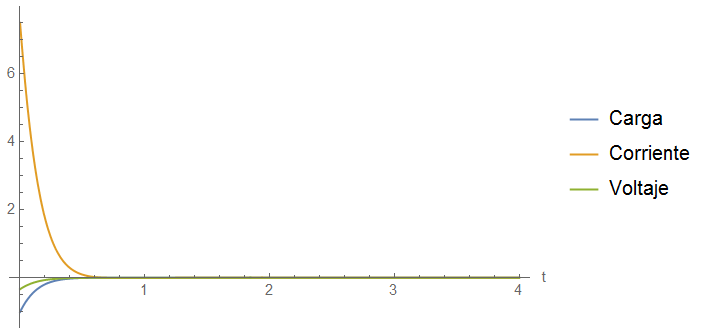
Cuando se tiene un amortiguamiento severo, es cuando $\gamma$ comienza a tener valores superiores a $\omega$, esto pasa porque la disipación de la energía es muy grande, eso hace que la carga y la corriente decrezcan de forma brusca.
En el amortiguamiento muy severo, predomina el comportamiento de la exponencial, incluso prácticamente ya no hay comportamiento de una vibración.
Energía
La energía se calcula igual, con las ecuaciones (\ref{l}) y (\ref{c}), pero ahora hay que usar las nuevas funciones para la carga y para la corriente, las cuales son (\ref{qr}) y (\ref{ir}). Ésta nueva forma de ver las funciones de carga y corriente nos darán por si mismas el cambio de la energía con el paso del tiempo, ya que tienen incluido el valor de la resistencia.
Para calcular el cambio de la energía, primero se hace la derivada total de ella
\begin{equation} \frac{d\mathcal{E}}{dt}=\frac{\partial \mathcal{E}}{\partial \dot{\psi}}\frac{\partial\dot{\psi}}{\partial t}+\frac{\partial\mathcal{E}}{\partial \psi }\frac{\partial \psi}{\partial t}. \end{equation}
Aplicando las derivadas a la la ecuación (\ref{eb}) queda
\begin{eqnarray*} \frac{d\mathcal{E}}{dt}=\left(L\ddot{\psi}+\frac{1}{C}\psi \right) \left( \dot{\psi}\right) \end{eqnarray*}
Se retoma la notación con $\psi$ para que sea todo más cómodo. Si se toma en cuenta (\ref{res}), lo que está adentro de los paréntesis de la expresión anterior es igual a $-RI$, retomando la relación de $\psi$ con la carga se puede expresar el cambio de la energía como
\begin{equation}
\frac{d\mathcal{E}}{dt}=-R\dot{q}^{2}=-RI^{2}.
\label{energia}
\end{equation}
Si la derivada de una función es negativa, quiere decir que la función decrece. Eso nos indica que la energía decrece y esto nos lo ilustra la expresión (\ref{energia}).
Como conclusión, la resistencia hace que se disipa energía, eso hace que todo decrezca y entre mayor sea la resistencia, decae más rápido la carga, el voltaje, la corriente y la energía.
Contribución:Juan Daniel Rivera Bautista (discusión) 21:49 12 jul 2020 (CDT)